浙教版 七年级数学下册 第二章 二元一次方程组 参数专题习题(word版 含答案)
文档属性
| 名称 | 浙教版 七年级数学下册 第二章 二元一次方程组 参数专题习题(word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 241.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-17 00:00:00 | ||
图片预览



文档简介
参数处理,柳暗花明
参数:设而不求,搭桥铺路
1.有一片牧场,草每天都在匀速地生长(即草每天增长的量相等),如果放牧24头牛,则6天吃完牧草;如果放牧21头牛,则8天吃完牧草.设每头牛每天吃草的量是相等的,如果放牧16头牛,则几天可以吃完牧草?
2. 小林沿着笔直的公路靠右匀速行走,发现每隔5分钟从背后驶过一辆101路公交车,每隔3分钟从迎面驶来一辆101路公交车.假设每辆101路公交车行驶速度相同,而且101路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是 .分钟.
3.自行车的轮胎安装在前轮上行驶3000千米后报废,安装在后轮上,只能行驶2000千米,为了行驶尽可能多的路程,采取在自行车行驶一定路程后,用前后轮调换使用的方法,那么安装在自行车上的这对轮胎最多可行驶多少千米?源:21·世纪·教育·网】
4.学校设置了有关艺术类的甲、乙、丙三个拓展性课程项目,规定甲、乙两项不能兼报,学生选报后作了统计,发现报甲项目的人数与报乙项目的人数之和为报丙项目人数的;同时兼报甲、丙两项目的人数占报甲项目的人数的,同时兼报乙、丙两项目的人数占报乙项目的人数的;兼报甲、丙两项目的人数与兼报乙、丙两项目的人数之和是报丙项目人数的,求报甲、乙两个项目的人数之比.
方程个数<字母个数--------参数处理
若是整数,关于的二元一次方程组的解是整数,求满足条件的所有的值
关于的二元一次方程组的解是正整数,求整数的值.
3.已知关于x、y的方程组给出下列结论:①是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④x,y的值都为自然数的解有4对,其中正确的有( )21cnjy.com
A.①③ B.②③ C.③④ D.②③④
nj*y.co*m】
】锁定参数,顺藤摸瓜
1.如果,其中xyz≠0,那么x:y:z=( )
A.1:2:3 B.2:3:4 C.2:3:1 D.3:2:1
网2.已知x+2y﹣3z=0,2x+3y+5z=0,则= .
版权所有
3.已知关于x,y的方程组
(1)请直接写出方程x+2y-6=0的所有正整数解;
(2)若方程组的解满足x+y=0,求m的值;
(3)无论实数m取何值时,方程x-2y+mx+5=0总有一个固定的解,求出这个解.
(4)若方程组的解中x恰为整数,m也为整数,求m的值.
4.已知关于的二元一次方程组给出下列结论:①当时,此方程组无解;②若此方程组的解也是方程的解,则;③无论整数k取何值,此方程组一定无整数解(均为整数),其中正确的是 ww.21-cn-jy.com
参数一来,难变易
1.已知关于x,y的二元一次方程.无论a取什么值时,方程都有一个公共的解,求这个公共解.教育网
2.已知关于x、y的二元一次方程(a﹣3)x+(2a﹣5)y+6﹣a=0,当a每取一个值时就有一个方程,这些方程有一个公共解,求这个公共解.
3.若且,则k的值为( )
A.1 B.2 C.3 D.4
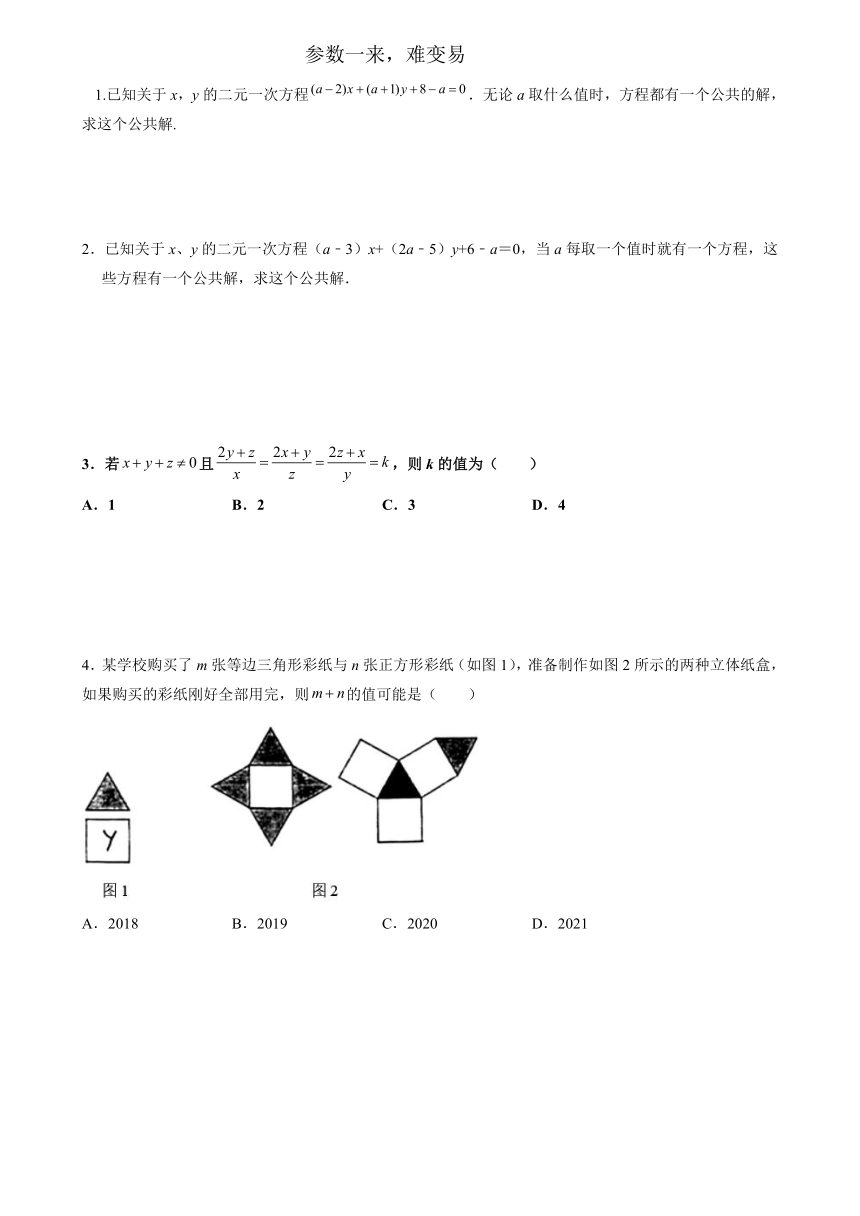
4.某学校购买了m张等边三角形彩纸与n张正方形彩纸(如图1),准备制作如图2所示的两种立体纸盒,如果购买的彩纸刚好全部用完,则的值可能是( )
A.2018 B.2019 C.2020 D.2021
参考答案:设而不求,搭桥铺路
1.有一片牧场,草每天都在匀速地生长(即草每天增长的量相等),如果放牧24头牛,则6天吃完牧草;如果放牧21头牛,则8天吃完牧草.设每头牛每天吃草的量是相等的,如果放牧16头牛,则几天可以吃完牧草?
解:设每头牛每天吃草x千克,牧场的草每天生长y千克,如果放牧16头牛,则m天可以吃完牧草,
依题意,得:,由①可得出:y=12x③,
将③代入②中,得:16mx﹣12mx=24×6x﹣6×12x,解得:m=18.
2. 小林沿着笔直的公路靠右匀速行走,发现每隔5分钟从背后驶过一辆101路公交车,每隔3分钟从迎面驶来一辆101路公交车.假设每辆101路公交车行驶速度相同,而且101路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是 .分钟.
解:设车的速度是a,人的速度是b,每隔t分钟发一班车,两辆车之间的距离是:at,
车从背后驶过是一个追及问题,人与车之间的距离也是:at,那么:at=5(a﹣b)①,
车从前面来是相遇问题,那么:at=3(a+b)②,①﹣②得:a=4b,所以:at=3.75a,
t=3.75,即发车的间隔的时间是3.75分钟,
3.自行车的轮胎安装在前轮上行驶3000千米后报废,安装在后轮上,只能行驶2000千米,为了行驶尽可能多的路程,采取在自行车行驶一定路程后,用前后轮调换使用的方法,那么安装在自行车上的这对轮胎最多可行驶多少千米?
解:设每个新轮胎报废时的总磨损量为k,则安装在前轮的轮胎每行驶1km磨损量为,安装在后轮的轮胎每行驶1km的磨损量为,又设一对新轮胎交换位置前走了xkm,交换位置后走了ykm.分别以一个轮胎的总磨损量为等量关系列方程,有
,两式相加,得,则x+y=2400,
∴安装在自行车上的这对轮胎最多可行驶2400千米.
4.学校设置了有关艺术类的甲、乙、丙三个拓展性课程项目,规定甲、乙两项不能兼报,学生选报后作了统计,发现报甲项目的人数与报乙项目的人数之和为报丙项目人数的;同时兼报甲、丙两项目的人数占报甲项目的人数的,同时兼报乙、丙两项目的人数占报乙项目的人数的;兼报甲、丙两项目的人数与兼报乙、丙两项目的人数之和是报丙项目人数的,求报甲、乙两个项目的人数之比为.
解:设报甲项目的有x人,报乙项目的有y人,报丙项目的有z人,
依题意得:由①得:将③代入②得:
化简得:∴x:y=1:2.故答案为:1:2.
参数:方程个数<字母个数
1.若是整数,关于的二元一次方程组的解是整数,求满足条件的所有的值
解:,两式相加得(m+3)x=10,解得x=,
∵m+3能被10整除,∴整数m=-13,-8,-5,-4,-2,-1,2,7,
当m=-13,-5,-1,7时,y不是整数,∴整数m=-8,-4,-2,2,
2.关于的二元一次方程组的解是正整数,求整数的值.
解:方程组,①×2 ②得:(4 k)y=8,解得:y=,
把y=代入①得:x=,由方程组的解为正整数,得到4 k=1,2,4,8,
解得:k=3,2,0, 4,代入x=,检验得:k=2, 4,0,
则整数k的值为 4,0,2.
3.已知关于x、y的方程组给出下列结论:①是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④x,y的值都为自然数的解有4对,其中正确的有( )
A.①③ B.②③ C.③④ D.②③④
解:①将x=5,y=﹣1代入方程组得:,由①得a=2,由②得a=,故①不正确.
②解方程①﹣②得:8y=4﹣4a解得:y=,将y的值代入①得:x=,
所以x+y=3,故无论a取何值,x、y的值都不可能互为相反数,故②正确.
③将a=1代入方程组得:,解此方程得:,
将x=3,y=0代入方程x+y=3,方程左边=3=右边,是方程的解,故③正确.
④因为x+y=3,所以x、y都为自然数的解有,,,.故④正确.
则正确的选项有②③④.故选:D.
锁定参数,顺藤摸瓜
1.如果,其中xyz≠0,那么x:y:z=( )
A.1:2:3 B.2:3:4 C.2:3:1 D.3:2:1
解:已知,①×2﹣②得,7y﹣21z=0,∴y=3z,
代入①得,x=8z﹣6z=2z,∴x:y:z=2z:3z:z=2:3:1.故选C.网
2.已知x+2y﹣3z=0,2x+3y+5z=0,则= .
解:由题意得:,①×2﹣②得y=11z,代入①得x=﹣19z,
原式===.故本题答案为:.
3.已知关于x,y的方程组 (1)请直接写出方程x+2y-6=0的所有正整数解;(2)若方程组的解满足x+y=0,求m的值;(3)无论实数m取何值时,方程x-2y+mx+5=0总有一个固定的解,求出这个解.(4)若方程组的解中x恰为整数,m也为整数,求m的值.
.
解:(1)
(2) 解得 把代入,解得m=
(3)(4)①+②得:
解得,∵x恰为整数,m也为整数,∴2+m=1或2+m=-1,解得
4.已知关于的二元一次方程组给出下列结论:①当时,此方程组无解;②若此方程组的解也是方程的解,则;③无论整数k取何值,此方程组一定无整数解(均为整数),其中正确的个数是
解:当时,方程组为,此时方程组无解;故①正确;
解方程组得:,把,代入,方程左右两边相等,故②正确;
解方程组得:,又为整数,若是整数,则,,2,,1,此时不是整数,x、不能均为整数,故③正确.
参数一来,难变易
1.已知关于x,y的二元一次方程.无论a取什么值时,方程都有一个公共的解,求这个公共解.
解:如果当a取一个确定的值时就得到一个方程,这些方程有一个公共解,说明无论a取何值,都不影响方程,即含a的项的系数相加为0.方程整理为ax﹣2x+ay+y+8﹣a=0,∴a(x+y﹣1)﹣2x+y+8=0.∵无论a取什么值时,方程都有一个公共的解,∴,解得:.
2.已知关于x、y的二元一次方程(a﹣3)x+(2a﹣5)y+6﹣a=0,当a每取一个值时就有一个方程,这些方程有一个公共解,求这个公共解是.
解:原方程可整理得:a(x+2y﹣1)+(6﹣3x﹣5y)=0,根据题意得:
,解得:,故答案为:.
3.若且,则k的值为( )
A.1 B.2 C.3 D.4
解:∵,
∴,∴①+②+③得:3(x+y+z)=k(x+y+z),
3(x+y+z) k(x+y+z)=0,3(x+y+z)(3 k)=0,
因为x+y+z不等于0,所以3 k=0,即k=3.故选:C.
21cnjy.com4.某学校购买了m张等边三角形彩纸与n张正方形彩纸(如图1),准备制作如图2所示的两种立体纸盒,如果购买的彩纸刚好全部用完,则的值可能是( )
A.2018 B.2019 C.2020 D.2021
解:设一共制作了x个四棱锥,y个三棱柱,根据题意可得:,
①+②,得5x+5y=m+n,∴5(x+y)=m+n,由此可知,m+n一定是5的倍数,
而2018,2019,2020,2021这四个数中,只有2020是5的倍数,
∴m+n的值可能是2020,故选:C.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
参数:设而不求,搭桥铺路
1.有一片牧场,草每天都在匀速地生长(即草每天增长的量相等),如果放牧24头牛,则6天吃完牧草;如果放牧21头牛,则8天吃完牧草.设每头牛每天吃草的量是相等的,如果放牧16头牛,则几天可以吃完牧草?
2. 小林沿着笔直的公路靠右匀速行走,发现每隔5分钟从背后驶过一辆101路公交车,每隔3分钟从迎面驶来一辆101路公交车.假设每辆101路公交车行驶速度相同,而且101路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是 .分钟.
3.自行车的轮胎安装在前轮上行驶3000千米后报废,安装在后轮上,只能行驶2000千米,为了行驶尽可能多的路程,采取在自行车行驶一定路程后,用前后轮调换使用的方法,那么安装在自行车上的这对轮胎最多可行驶多少千米?源:21·世纪·教育·网】
4.学校设置了有关艺术类的甲、乙、丙三个拓展性课程项目,规定甲、乙两项不能兼报,学生选报后作了统计,发现报甲项目的人数与报乙项目的人数之和为报丙项目人数的;同时兼报甲、丙两项目的人数占报甲项目的人数的,同时兼报乙、丙两项目的人数占报乙项目的人数的;兼报甲、丙两项目的人数与兼报乙、丙两项目的人数之和是报丙项目人数的,求报甲、乙两个项目的人数之比.
方程个数<字母个数--------参数处理
若是整数,关于的二元一次方程组的解是整数,求满足条件的所有的值
关于的二元一次方程组的解是正整数,求整数的值.
3.已知关于x、y的方程组给出下列结论:①是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④x,y的值都为自然数的解有4对,其中正确的有( )21cnjy.com
A.①③ B.②③ C.③④ D.②③④
nj*y.co*m】
】锁定参数,顺藤摸瓜
1.如果,其中xyz≠0,那么x:y:z=( )
A.1:2:3 B.2:3:4 C.2:3:1 D.3:2:1
网2.已知x+2y﹣3z=0,2x+3y+5z=0,则= .
版权所有
3.已知关于x,y的方程组
(1)请直接写出方程x+2y-6=0的所有正整数解;
(2)若方程组的解满足x+y=0,求m的值;
(3)无论实数m取何值时,方程x-2y+mx+5=0总有一个固定的解,求出这个解.
(4)若方程组的解中x恰为整数,m也为整数,求m的值.
4.已知关于的二元一次方程组给出下列结论:①当时,此方程组无解;②若此方程组的解也是方程的解,则;③无论整数k取何值,此方程组一定无整数解(均为整数),其中正确的是 ww.21-cn-jy.com
参数一来,难变易
1.已知关于x,y的二元一次方程.无论a取什么值时,方程都有一个公共的解,求这个公共解.教育网
2.已知关于x、y的二元一次方程(a﹣3)x+(2a﹣5)y+6﹣a=0,当a每取一个值时就有一个方程,这些方程有一个公共解,求这个公共解.
3.若且,则k的值为( )
A.1 B.2 C.3 D.4
4.某学校购买了m张等边三角形彩纸与n张正方形彩纸(如图1),准备制作如图2所示的两种立体纸盒,如果购买的彩纸刚好全部用完,则的值可能是( )
A.2018 B.2019 C.2020 D.2021
参考答案:设而不求,搭桥铺路
1.有一片牧场,草每天都在匀速地生长(即草每天增长的量相等),如果放牧24头牛,则6天吃完牧草;如果放牧21头牛,则8天吃完牧草.设每头牛每天吃草的量是相等的,如果放牧16头牛,则几天可以吃完牧草?
解:设每头牛每天吃草x千克,牧场的草每天生长y千克,如果放牧16头牛,则m天可以吃完牧草,
依题意,得:,由①可得出:y=12x③,
将③代入②中,得:16mx﹣12mx=24×6x﹣6×12x,解得:m=18.
2. 小林沿着笔直的公路靠右匀速行走,发现每隔5分钟从背后驶过一辆101路公交车,每隔3分钟从迎面驶来一辆101路公交车.假设每辆101路公交车行驶速度相同,而且101路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是 .分钟.
解:设车的速度是a,人的速度是b,每隔t分钟发一班车,两辆车之间的距离是:at,
车从背后驶过是一个追及问题,人与车之间的距离也是:at,那么:at=5(a﹣b)①,
车从前面来是相遇问题,那么:at=3(a+b)②,①﹣②得:a=4b,所以:at=3.75a,
t=3.75,即发车的间隔的时间是3.75分钟,
3.自行车的轮胎安装在前轮上行驶3000千米后报废,安装在后轮上,只能行驶2000千米,为了行驶尽可能多的路程,采取在自行车行驶一定路程后,用前后轮调换使用的方法,那么安装在自行车上的这对轮胎最多可行驶多少千米?
解:设每个新轮胎报废时的总磨损量为k,则安装在前轮的轮胎每行驶1km磨损量为,安装在后轮的轮胎每行驶1km的磨损量为,又设一对新轮胎交换位置前走了xkm,交换位置后走了ykm.分别以一个轮胎的总磨损量为等量关系列方程,有
,两式相加,得,则x+y=2400,
∴安装在自行车上的这对轮胎最多可行驶2400千米.
4.学校设置了有关艺术类的甲、乙、丙三个拓展性课程项目,规定甲、乙两项不能兼报,学生选报后作了统计,发现报甲项目的人数与报乙项目的人数之和为报丙项目人数的;同时兼报甲、丙两项目的人数占报甲项目的人数的,同时兼报乙、丙两项目的人数占报乙项目的人数的;兼报甲、丙两项目的人数与兼报乙、丙两项目的人数之和是报丙项目人数的,求报甲、乙两个项目的人数之比为.
解:设报甲项目的有x人,报乙项目的有y人,报丙项目的有z人,
依题意得:由①得:将③代入②得:
化简得:∴x:y=1:2.故答案为:1:2.
参数:方程个数<字母个数
1.若是整数,关于的二元一次方程组的解是整数,求满足条件的所有的值
解:,两式相加得(m+3)x=10,解得x=,
∵m+3能被10整除,∴整数m=-13,-8,-5,-4,-2,-1,2,7,
当m=-13,-5,-1,7时,y不是整数,∴整数m=-8,-4,-2,2,
2.关于的二元一次方程组的解是正整数,求整数的值.
解:方程组,①×2 ②得:(4 k)y=8,解得:y=,
把y=代入①得:x=,由方程组的解为正整数,得到4 k=1,2,4,8,
解得:k=3,2,0, 4,代入x=,检验得:k=2, 4,0,
则整数k的值为 4,0,2.
3.已知关于x、y的方程组给出下列结论:①是方程组的解;②无论a取何值,x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④x,y的值都为自然数的解有4对,其中正确的有( )
A.①③ B.②③ C.③④ D.②③④
解:①将x=5,y=﹣1代入方程组得:,由①得a=2,由②得a=,故①不正确.
②解方程①﹣②得:8y=4﹣4a解得:y=,将y的值代入①得:x=,
所以x+y=3,故无论a取何值,x、y的值都不可能互为相反数,故②正确.
③将a=1代入方程组得:,解此方程得:,
将x=3,y=0代入方程x+y=3,方程左边=3=右边,是方程的解,故③正确.
④因为x+y=3,所以x、y都为自然数的解有,,,.故④正确.
则正确的选项有②③④.故选:D.
锁定参数,顺藤摸瓜
1.如果,其中xyz≠0,那么x:y:z=( )
A.1:2:3 B.2:3:4 C.2:3:1 D.3:2:1
解:已知,①×2﹣②得,7y﹣21z=0,∴y=3z,
代入①得,x=8z﹣6z=2z,∴x:y:z=2z:3z:z=2:3:1.故选C.网
2.已知x+2y﹣3z=0,2x+3y+5z=0,则= .
解:由题意得:,①×2﹣②得y=11z,代入①得x=﹣19z,
原式===.故本题答案为:.
3.已知关于x,y的方程组 (1)请直接写出方程x+2y-6=0的所有正整数解;(2)若方程组的解满足x+y=0,求m的值;(3)无论实数m取何值时,方程x-2y+mx+5=0总有一个固定的解,求出这个解.(4)若方程组的解中x恰为整数,m也为整数,求m的值.
.
解:(1)
(2) 解得 把代入,解得m=
(3)(4)①+②得:
解得,∵x恰为整数,m也为整数,∴2+m=1或2+m=-1,解得
4.已知关于的二元一次方程组给出下列结论:①当时,此方程组无解;②若此方程组的解也是方程的解,则;③无论整数k取何值,此方程组一定无整数解(均为整数),其中正确的个数是
解:当时,方程组为,此时方程组无解;故①正确;
解方程组得:,把,代入,方程左右两边相等,故②正确;
解方程组得:,又为整数,若是整数,则,,2,,1,此时不是整数,x、不能均为整数,故③正确.
参数一来,难变易
1.已知关于x,y的二元一次方程.无论a取什么值时,方程都有一个公共的解,求这个公共解.
解:如果当a取一个确定的值时就得到一个方程,这些方程有一个公共解,说明无论a取何值,都不影响方程,即含a的项的系数相加为0.方程整理为ax﹣2x+ay+y+8﹣a=0,∴a(x+y﹣1)﹣2x+y+8=0.∵无论a取什么值时,方程都有一个公共的解,∴,解得:.
2.已知关于x、y的二元一次方程(a﹣3)x+(2a﹣5)y+6﹣a=0,当a每取一个值时就有一个方程,这些方程有一个公共解,求这个公共解是.
解:原方程可整理得:a(x+2y﹣1)+(6﹣3x﹣5y)=0,根据题意得:
,解得:,故答案为:.
3.若且,则k的值为( )
A.1 B.2 C.3 D.4
解:∵,
∴,∴①+②+③得:3(x+y+z)=k(x+y+z),
3(x+y+z) k(x+y+z)=0,3(x+y+z)(3 k)=0,
因为x+y+z不等于0,所以3 k=0,即k=3.故选:C.
21cnjy.com4.某学校购买了m张等边三角形彩纸与n张正方形彩纸(如图1),准备制作如图2所示的两种立体纸盒,如果购买的彩纸刚好全部用完,则的值可能是( )
A.2018 B.2019 C.2020 D.2021
解:设一共制作了x个四棱锥,y个三棱柱,根据题意可得:,
①+②,得5x+5y=m+n,∴5(x+y)=m+n,由此可知,m+n一定是5的倍数,
而2018,2019,2020,2021这四个数中,只有2020是5的倍数,
∴m+n的值可能是2020,故选:C.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
