3.4乘法公式(2) 课件(共21张PPT)
文档属性
| 名称 | 3.4乘法公式(2) 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-18 09:16:41 | ||
图片预览








文档简介
(共21张PPT)
3.4乘法公式
第2课时
浙教版 七年级下
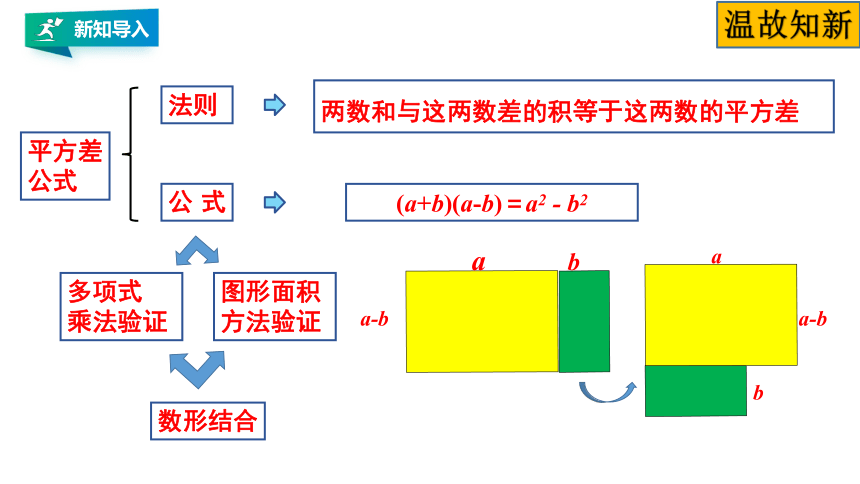
平方差
公式
法则
两数和与这两数差的积等于这两数的平方差
公式
图形面积方法验证
多项式
乘法验证
数形结合
a
b
b
a
a-b
a-b
温故知新
(a+b)(a-b)=a2 - b2
新知导入
温故知新
计算:
观察上述三小题的计算,你发现有什么规律?
(x+2)(x-2)
= x 2- 4
新知导入
猜
想
探究公式一
三项
两数和的平方
新知探究
(a+b)2
=(a+b)(a+b)
=a2+ab+ab+b2
=a2+2ab+b2
是否正确?
(a+b)2=a2+2ab+b2
验证公式
证明
用多项式相乘法则
验证
用图形面积方法
(代数法)
(几何法)
新知讲解
多项式相乘法则
b
a
n
m
am
nm
nb
ab
验证
类比
两数和的完全平方公式
(a+b)2=a2+2ab+b2
a
a
b
b
ab
ab
a2
b2
验证
验证公式
数形结合
新知讲解
猜想2:
两数和的平方,等于这两数的平方和,加上这两数积的2倍.
两数和的完全平方公式:
(a+b)2=a2+2ab+b2
探究公式二
a2 - 2ab+b2
=(a-b)(a-b)
=a2-ab-ab+b2
2.是否可以写成[a+(-b)]2
1.(a-b)2
=a2 - 2ab+b2
a
a
b
b
b
b
a-b
a-b
3.图形面积验证
(a-b)2= a2 - 2ab+b2
=a2+2a ( b)+ ( b)2
=a2 - 2ab+b2
(a b)2
=[a+( b)]2
证明
换元思想
数形结合
归纳:
新知探究
归纳1
两数和的完全平方公式与两数差的
完全平方公式,统称完全平方公式.
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
(首±尾)2=首2±2×首×尾+尾2
平方差公式和完全平方公式也称乘法公式.
完全平方有三项,
首平方,尾平方,
首尾两倍中间放。
两数和的平方,等于这两数的平方和,加上这两数积的2倍.
两数差的平方,等于这两数的平方和,减去这两数积的2倍.
归纳小结1
新知讲解
填一填:
(1)(a+1)2=( )2+2( )( )+( )2
=( )
(2)(2a-3b)2=( )2-2( )( )+( )2
=( )
a2+2a+1
两数和的完全平方公式 (a+b)2 = a2+2ab+b2 .
两数差的完全平方公式 (a b)2 = a2 2ab+b2 .
4a2-12ab+9b2
理解公式
完全平方有三项,
首平方,尾平方,
首尾两倍中间放。
a
a
1
1
2a
3b
2a
3b
公式中的a和b可以是一个数,一个字母,也可以是单项式,甚至更复杂的代数式,计算时要有整体思想.
新知讲解
下列各式的计算是否有错?错的请改正。
(1) (x+y)2 = x2 +y2
(2) (a –b)2 = a2 -b2
(3) (x– 1)2 = x2 – 2x
(4) (a+2b)2 = a2+2ab+2b2
两数和的完全平方公式 (a+b)2 = a2+2ab+b2 .
两数差的完全平方公式 (a b)2 = a2 2ab+b2 .
理解公式
完全平方有三项,
首平方,尾平方,
首尾两倍中间放。
新知讲解
应用公式
1.直接应用
例3: 用完全平方公式计算:
(1)(x+2 y)2 .
(2)(2 a-5)2 .
解 (1)(x+2 y)2
=x2 +2· x·2 y+(2 y)2
=x2 +4 x y+4 y 2 .
(2)(2a-5)2
=(2 a)2 -2·2 a·5+52
=4 a2 -20 a+25.
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
例题讲解
(3)(-2 s+t)2
=(-2 s) 2 +2·(-2 s ) · t+ t 2
=4 s 2 -4 s t+t 2 .
应用公式
=(-3x)2 -2·(-3 x)· 4 y+(4 y)2
=9 x 2 +24 x y+16 y 2
(4)(-3x-4 y)2
(3)(-2 s+t)2
=(t-2 s)2
=t 2 -2· t ·2 s+(2 s)2
=t 2 -4 t s+4 s 2 .
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
(4)(-3x-4 y)2
=(-3x)2 +2·(-3x)·(- 4 y)+(- 4 y)2
=9 x 2 +24 x y+16 y 2
(3)(-2 s+t)2 .
(4)(-3 x-4 y)2 .
例题讲解
归纳2
首尾平方总得正;
中间符号看首尾项的积,同号得正,异号得负,中间的2倍要记牢;
进而总结步骤为:
(1).确定首尾,分别平方;
(2).确定中间项的系数和符号;
(3).写出答案。
(1)(x+2y)2 =x 2 +4 x y +4 y 2
(2)(2 a-5)2
=4 a 2 -20 a +25
(3)(-2 s+t)2
=4 s 2 -4 s t + t 2
(4)(-3 x -4 y)2
=9 x 2 +24 x y +16 y 2
归纳小结2
同号得正
异号得负
首尾平方总得正
归纳小结
2.选择应用
选择适当的乘法公式计算:
(1)(2x-1)(-1+2x) (2)(-2x-y)(2x-y) (3)(-a+5)(-a-5) (4)(ab-1)(-ab+1)
应用公式
解:原式=(2x-1)2
=4x2-4x+1
解:原式=-(ab-1)2
=-(a2b2-2ab+1)
=-a2b2+2ab-1
1.观察符号
2.适当变形
3.选择公式
4.注意括号
解:原式=(-y)2-(2x)2
= y2-4y2
解:原式=(-a)2-52
= a2-25
平方差公式:
(a+b)(a-b)=a2 - b2
1.平方差公式
2.完全平方公式
课堂练习
3.简便应用
用简便方法计算:
(1)982 (2)20202-2019×4040+20192
解:原式 =( 100 2)2
= 1002 2 ×100×2 + 22
= 9604
= 10000 400 +4
原式 = ( 2020-2019 )2
= 12
= 1
(a-b)2= a2 - 2ab+b2
应用公式
公式逆用
课堂练习
4.综合应用
例4:一花农有2块正方形茶花苗圃,边长分别为 30.1m ,29.5 m,现将这2块苗圃的边长都增加1.5m后,求各苗圃的面积分别增加了多少m2
解:设原正方形苗圃的边长为a(m),
边长增加1.5m后,新正方形的边长
为(a+1.5)m;由题意可得,
当a=30.1时,3a+2.25=3×30.1+2.25=92.55;
当a=29.5时,3a+2.25=3×29.5+2.25=90.75;
答:两块苗圃的面积分别增加了92.55平方米,90.75平方米。
a
a
1.5
1.5
先化简再求值的思想方法
例题讲解
5.灵活应用
1.如果多项式x2+kx+25是完全平方式,求k 的值。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
解:a2+b2=(a+b)2-2ab
=52-2×5×(-3)
=25+30
=55
(2)解法二(a-b)2=(a+b)2 -4ab
=52-4×5×(-3)
=25+60
=85
(2)解法一(a-b)2=a2 - 2ab+b2
=55-2×5×(-3)
=55+30
=85
2.若a+b=5,ab=-3,求(1)a2+b2; ( 2 ) (a-b)2
(3)a2-ab+b2
(3)解法一a2-ab+b2
=55-5×(-3)
=55+15
=70
(3)解法二a2-ab+b2=(a+b)2 -3ab
=52-3×5×(-3)
=25+45
=70
应用公式
拓展提升
课堂总结
乘法公式
完全平方公式
平方差公式
(a+b)(a-b)=a2 - b2
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
类比学习
a2+b2=(a+b)2-2ab
(a-b)2=(a+b)2 -4ab
注意区别,
灵活应用
巧妙变形,
熟练应用
完全平方有三项,
首平方,尾平方,
首尾两倍中间放。
熟记口诀,
直接应用
多项式乘法
换元思想
课堂总结
完成作业本(2)3.4乘法公式(2)
作业布置
作业布置
https://www.21cnjy.com/help/help_extract.php
3.4乘法公式
第2课时
浙教版 七年级下
平方差
公式
法则
两数和与这两数差的积等于这两数的平方差
公式
图形面积方法验证
多项式
乘法验证
数形结合
a
b
b
a
a-b
a-b
温故知新
(a+b)(a-b)=a2 - b2
新知导入
温故知新
计算:
观察上述三小题的计算,你发现有什么规律?
(x+2)(x-2)
= x 2- 4
新知导入
猜
想
探究公式一
三项
两数和的平方
新知探究
(a+b)2
=(a+b)(a+b)
=a2+ab+ab+b2
=a2+2ab+b2
是否正确?
(a+b)2=a2+2ab+b2
验证公式
证明
用多项式相乘法则
验证
用图形面积方法
(代数法)
(几何法)
新知讲解
多项式相乘法则
b
a
n
m
am
nm
nb
ab
验证
类比
两数和的完全平方公式
(a+b)2=a2+2ab+b2
a
a
b
b
ab
ab
a2
b2
验证
验证公式
数形结合
新知讲解
猜想2:
两数和的平方,等于这两数的平方和,加上这两数积的2倍.
两数和的完全平方公式:
(a+b)2=a2+2ab+b2
探究公式二
a2 - 2ab+b2
=(a-b)(a-b)
=a2-ab-ab+b2
2.是否可以写成[a+(-b)]2
1.(a-b)2
=a2 - 2ab+b2
a
a
b
b
b
b
a-b
a-b
3.图形面积验证
(a-b)2= a2 - 2ab+b2
=a2+2a ( b)+ ( b)2
=a2 - 2ab+b2
(a b)2
=[a+( b)]2
证明
换元思想
数形结合
归纳:
新知探究
归纳1
两数和的完全平方公式与两数差的
完全平方公式,统称完全平方公式.
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
(首±尾)2=首2±2×首×尾+尾2
平方差公式和完全平方公式也称乘法公式.
完全平方有三项,
首平方,尾平方,
首尾两倍中间放。
两数和的平方,等于这两数的平方和,加上这两数积的2倍.
两数差的平方,等于这两数的平方和,减去这两数积的2倍.
归纳小结1
新知讲解
填一填:
(1)(a+1)2=( )2+2( )( )+( )2
=( )
(2)(2a-3b)2=( )2-2( )( )+( )2
=( )
a2+2a+1
两数和的完全平方公式 (a+b)2 = a2+2ab+b2 .
两数差的完全平方公式 (a b)2 = a2 2ab+b2 .
4a2-12ab+9b2
理解公式
完全平方有三项,
首平方,尾平方,
首尾两倍中间放。
a
a
1
1
2a
3b
2a
3b
公式中的a和b可以是一个数,一个字母,也可以是单项式,甚至更复杂的代数式,计算时要有整体思想.
新知讲解
下列各式的计算是否有错?错的请改正。
(1) (x+y)2 = x2 +y2
(2) (a –b)2 = a2 -b2
(3) (x– 1)2 = x2 – 2x
(4) (a+2b)2 = a2+2ab+2b2
两数和的完全平方公式 (a+b)2 = a2+2ab+b2 .
两数差的完全平方公式 (a b)2 = a2 2ab+b2 .
理解公式
完全平方有三项,
首平方,尾平方,
首尾两倍中间放。
新知讲解
应用公式
1.直接应用
例3: 用完全平方公式计算:
(1)(x+2 y)2 .
(2)(2 a-5)2 .
解 (1)(x+2 y)2
=x2 +2· x·2 y+(2 y)2
=x2 +4 x y+4 y 2 .
(2)(2a-5)2
=(2 a)2 -2·2 a·5+52
=4 a2 -20 a+25.
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
例题讲解
(3)(-2 s+t)2
=(-2 s) 2 +2·(-2 s ) · t+ t 2
=4 s 2 -4 s t+t 2 .
应用公式
=(-3x)2 -2·(-3 x)· 4 y+(4 y)2
=9 x 2 +24 x y+16 y 2
(4)(-3x-4 y)2
(3)(-2 s+t)2
=(t-2 s)2
=t 2 -2· t ·2 s+(2 s)2
=t 2 -4 t s+4 s 2 .
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
(4)(-3x-4 y)2
=(-3x)2 +2·(-3x)·(- 4 y)+(- 4 y)2
=9 x 2 +24 x y+16 y 2
(3)(-2 s+t)2 .
(4)(-3 x-4 y)2 .
例题讲解
归纳2
首尾平方总得正;
中间符号看首尾项的积,同号得正,异号得负,中间的2倍要记牢;
进而总结步骤为:
(1).确定首尾,分别平方;
(2).确定中间项的系数和符号;
(3).写出答案。
(1)(x+2y)2 =x 2 +4 x y +4 y 2
(2)(2 a-5)2
=4 a 2 -20 a +25
(3)(-2 s+t)2
=4 s 2 -4 s t + t 2
(4)(-3 x -4 y)2
=9 x 2 +24 x y +16 y 2
归纳小结2
同号得正
异号得负
首尾平方总得正
归纳小结
2.选择应用
选择适当的乘法公式计算:
(1)(2x-1)(-1+2x) (2)(-2x-y)(2x-y) (3)(-a+5)(-a-5) (4)(ab-1)(-ab+1)
应用公式
解:原式=(2x-1)2
=4x2-4x+1
解:原式=-(ab-1)2
=-(a2b2-2ab+1)
=-a2b2+2ab-1
1.观察符号
2.适当变形
3.选择公式
4.注意括号
解:原式=(-y)2-(2x)2
= y2-4y2
解:原式=(-a)2-52
= a2-25
平方差公式:
(a+b)(a-b)=a2 - b2
1.平方差公式
2.完全平方公式
课堂练习
3.简便应用
用简便方法计算:
(1)982 (2)20202-2019×4040+20192
解:原式 =( 100 2)2
= 1002 2 ×100×2 + 22
= 9604
= 10000 400 +4
原式 = ( 2020-2019 )2
= 12
= 1
(a-b)2= a2 - 2ab+b2
应用公式
公式逆用
课堂练习
4.综合应用
例4:一花农有2块正方形茶花苗圃,边长分别为 30.1m ,29.5 m,现将这2块苗圃的边长都增加1.5m后,求各苗圃的面积分别增加了多少m2
解:设原正方形苗圃的边长为a(m),
边长增加1.5m后,新正方形的边长
为(a+1.5)m;由题意可得,
当a=30.1时,3a+2.25=3×30.1+2.25=92.55;
当a=29.5时,3a+2.25=3×29.5+2.25=90.75;
答:两块苗圃的面积分别增加了92.55平方米,90.75平方米。
a
a
1.5
1.5
先化简再求值的思想方法
例题讲解
5.灵活应用
1.如果多项式x2+kx+25是完全平方式,求k 的值。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
解:a2+b2=(a+b)2-2ab
=52-2×5×(-3)
=25+30
=55
(2)解法二(a-b)2=(a+b)2 -4ab
=52-4×5×(-3)
=25+60
=85
(2)解法一(a-b)2=a2 - 2ab+b2
=55-2×5×(-3)
=55+30
=85
2.若a+b=5,ab=-3,求(1)a2+b2; ( 2 ) (a-b)2
(3)a2-ab+b2
(3)解法一a2-ab+b2
=55-5×(-3)
=55+15
=70
(3)解法二a2-ab+b2=(a+b)2 -3ab
=52-3×5×(-3)
=25+45
=70
应用公式
拓展提升
课堂总结
乘法公式
完全平方公式
平方差公式
(a+b)(a-b)=a2 - b2
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
类比学习
a2+b2=(a+b)2-2ab
(a-b)2=(a+b)2 -4ab
注意区别,
灵活应用
巧妙变形,
熟练应用
完全平方有三项,
首平方,尾平方,
首尾两倍中间放。
熟记口诀,
直接应用
多项式乘法
换元思想
课堂总结
完成作业本(2)3.4乘法公式(2)
作业布置
作业布置
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
