2022年浙教版七年级下册5.5分式方程的应用 课件(18张)
文档属性
| 名称 | 2022年浙教版七年级下册5.5分式方程的应用 课件(18张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 16:30:11 | ||
图片预览





文档简介
(共18张PPT)
分式方程的应用
学习目标
◆ 1. 会根据具体问题中的数量关系列出分式方程,体会分式方程是刻画现实世界数量关系的有效模型;
◆ 2. 会根据具体问题的实际意义检验方程解是否合理;
◆ 3. 会解决一些与分式方程有关的实际问题,发展分析问题,解决问题的能力和应用意识.
引入新课
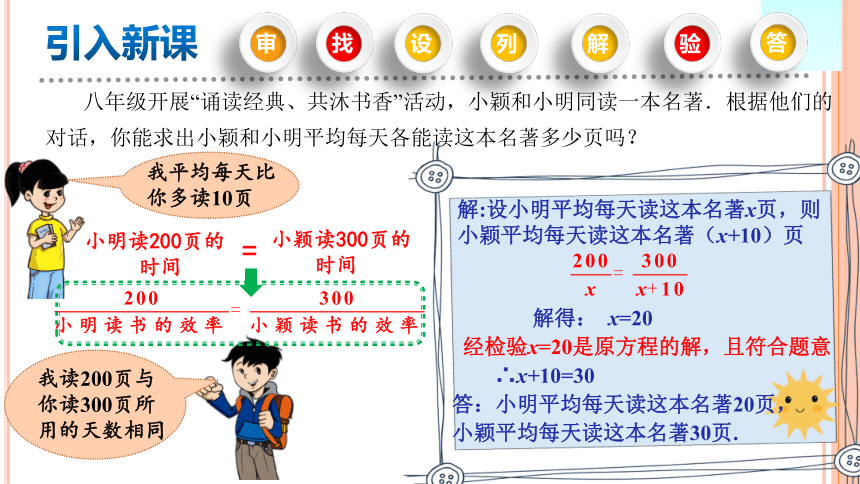
八年级开展“诵读经典、共沐书香”活动,小颖和小明同读一本名著.根据他们的
对话,你能求出小颖和小明平均每天各能读这本名著多少页吗?
我平均每天比你多读10页
我读200页与你读300页所用的天数相同
解得: x=20
经检验x=20是原方程的解,且符合题意
∴x+10=30
答:小明平均每天读这本名著20页,
小颖平均每天读这本名著30页.
解:设小明平均每天读这本名著x页,则
小颖平均每天读这本名著(x+10)页
检验:当x=20时,x(x+10)≠0,左边=右边
∴x=20是所列方程的根,且符合实际意义
审
找
设
解
验
答
列
小颖读300页的
时间
小明读200页的
时间
=
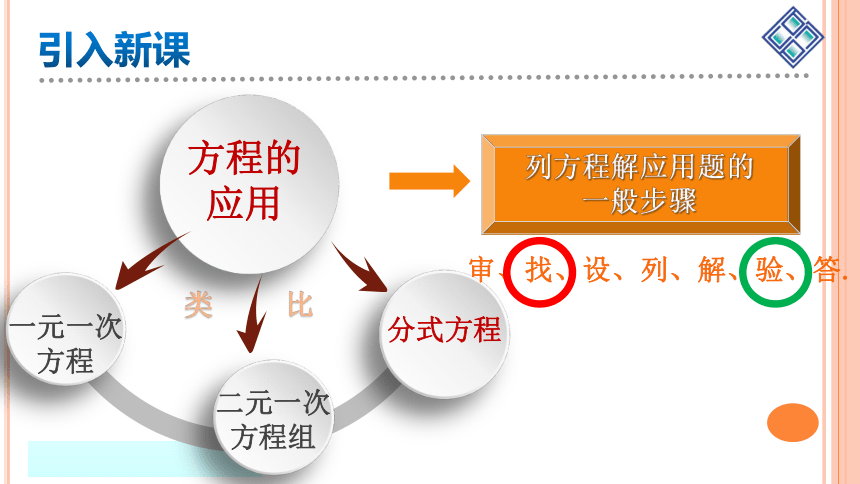
引入新课
二元一次方程组
分式方程
方程的应用
类 比
一元一次方程
列方程解应用题的
一般步骤
审、找、设、列、解、验、答.
问题情境
某单位将沿街的一部分房屋出租. 每间房屋的租金第二年比第一年
多500元,所有房屋出租的租金第一年为9.6万元,第二年为10.2万元.
1.你能找出这一情境中的等量关系吗
2.根据这一情境你能提出哪些问题
3.你能利用方程求出上面提出的问题吗
②第二年每间房屋的租金-第一年每间房屋的租金 =500元
③第一年出租房屋间数 = 第二年出租的房屋间数
①出租房屋间数=
问题1、求出租的房屋总间数;
问题2、分别求这两年每间房屋的租金.
注:先找基础三者关系,再从
这三个量中分别寻找条件.
解决问题
某单位将沿街的一部分房屋出租. 每间房屋的租金第二年比第一年
多500元,所有房屋出租的租金第一年为9.6万元,第二年为10.2万元.
问题1、求出租的房屋总间数;
解:设出租的房屋总间数为x间,
由题意得:
解得 :x=12.
经检验,x=12是原方程的解,且符合题意
答:出租的房屋总间数为12间.
千万不要忘记写检验哟!
解决问题
某单位将沿街的一部分房屋出租. 每间房屋的租金第二年比第一年
多500元,所有房屋出租的租金第一年为9.6万元,第二年为10.2万元.
问题2、分别求这两年每间房屋的租金.
解:设第一年每间房屋的租金为y元,则第二年每间房屋的租金为(y+500)元,根据题意,得
间数 每间房屋的租金 总租金
第一年
第二年
解决问题
某单位将沿街的一部分房屋出租. 每间房屋的租金第二年比第一年
多500元,所有房屋出租的租金第一年为9.6万元,第二年为10.2万元.
问题2、分别求这两年每间房屋的租金.
解:设第一年每间房屋的租金为y元,则第二年每间房屋的租金为(y+500)元,由题意得:
解得: y=8000
经检验,y=8000是原方程的解,且符合题意
y+500=8500.
答:第一年每间房屋的租金为8000元,第二年每间房屋的租金为8500元.
(1)审:审清题意;
(2)找:找出等量关系;
(3)设:设出未知数(直接设法、间接设法);
(5)解:解分式方程;
(7)答:写出答案.
(4)列:用代数式表示等量关系,列出分式方程;
(6)检:必须检验根的正确性与合理性;
归纳
列分式方程解应用题的步骤
验!验!验!
最重要!
巩固练习
1. 小明和同学一起去书店买书,他们先用15元买了一种科普书,又用15元
买了一种文学书. 科普书的价格比文学书高出一半,因此他们所买的科普书
比所买的文学书少1本. 这种科普书和这种文学书的价格各是多少
等量关系:
1.书本数=
2.科普书价格=文学书价格×1.5
3.所买文学书本数-所买的科普书本数=1
解:设文学书的价格是每本x元,则
科普书的价格是每本1.5x元.
由题意得:
解得 : x=5
经检验,x=5是原方程的解,且符合题意.
∴1.5x=1.5×5=7.5
答:文学书的价格是每本5元,
科普书的价格是每本7.5元.
巩固练习
2. 某商店销售一批服装,每件售价350元,可获利25%,求这种服装的成本价.
设这种服装的成本价为x元,则可列方程为( )
A.x=350×25% B.25%×x=350 C. D.350﹣x=25%
3.港珠澳大桥是我国桥梁建筑史上的又一伟大奇迹,东接香港,西接珠海、澳
门,全程55千米.通车前需走水陆两路共约170千米,通车后,约减少时间
3小时,平均速度是原来的2.5倍,如果设原来通车前的平均时速为x千米/小时,
则可列方程为 .
巩固练习
2. 某商店销售一批服装,每件售价150元,可获利25%,求这种服装的成本价.设这种服装的成本价为x元,则得到方程( )
A.x=150×25% B.25%×x=150 C. D.150﹣x=25%
C
利润问题:利润=售价-进价,利润率= ×100%
利润=150-x
分式方程
整式方程
能力提升
4.两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成. 哪个队的施工速度快?
表格法分析:
工作时间(月) 工作效率 工作量
甲队
乙队
等量关系:
甲队完成的工作总量+乙队完成的工作总量=“1”
设乙单独完成这项工程需要x个月.
此时,列方程为:
能力提升
4.两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成. 哪个队的施工速度快?
解:设乙单独完成这项工程需要x个月. 记工作总量为1,甲的工作效率是 ,
由题意得:
化简得:
解得 :x=1.
经检验x=1是原方程的解,且符合题意.
∵乙队单独施工1个月可以完成全部任务,而甲队单独施工需3个月才可以完成全部任务,
∴乙队的施工速度快.
能力提升
4.两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成. 哪个队的施工速度快?
想一想:本题的列方程所用的等量关系还可以怎么找?
甲队单独完成的工作总量+两队合作完成的工作总量=“1”
工作时间 工作效率 工作量
甲单独
两队合作
设乙单独完成这项工程需要x天.
此时,列方程为:
1
课堂小结
实际问题
找等量关系
设未知数、列方程
数学问题
(分式方程)
解方程
方程的解
检验
实际问题
的答案
建模
(1)收费问题:总价=单价×数量
(2)利润问题:利润=售价-进价,利润率= ×100%
(3)行程问题: 路程=速度×时间
(4)工程问题:工作量=工作效率×工作时间
……
基本等量关系
课堂小结
和(差)、倍(分)
当堂检测
利用分式方程解决下列问题:
为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买A种图书花费了3000元,购买B种图书花费了1600元,A种图书的
单价是B种图书的1.5倍,购买A种图书的数量比B种图书多20本.求A和B
两种图书的单价.
解:(1)设B种图书的单价为x元,则A种图书的单价为1.5x元,
由题意得:
解得: x=20,
经检验,x=20是所列方程的解,且符合题意,
∴1.5x=30.
答:A种图书的单价为30元,B种图书的单价为20元.
分式方程的应用
学习目标
◆ 1. 会根据具体问题中的数量关系列出分式方程,体会分式方程是刻画现实世界数量关系的有效模型;
◆ 2. 会根据具体问题的实际意义检验方程解是否合理;
◆ 3. 会解决一些与分式方程有关的实际问题,发展分析问题,解决问题的能力和应用意识.
引入新课
八年级开展“诵读经典、共沐书香”活动,小颖和小明同读一本名著.根据他们的
对话,你能求出小颖和小明平均每天各能读这本名著多少页吗?
我平均每天比你多读10页
我读200页与你读300页所用的天数相同
解得: x=20
经检验x=20是原方程的解,且符合题意
∴x+10=30
答:小明平均每天读这本名著20页,
小颖平均每天读这本名著30页.
解:设小明平均每天读这本名著x页,则
小颖平均每天读这本名著(x+10)页
检验:当x=20时,x(x+10)≠0,左边=右边
∴x=20是所列方程的根,且符合实际意义
审
找
设
解
验
答
列
小颖读300页的
时间
小明读200页的
时间
=
引入新课
二元一次方程组
分式方程
方程的应用
类 比
一元一次方程
列方程解应用题的
一般步骤
审、找、设、列、解、验、答.
问题情境
某单位将沿街的一部分房屋出租. 每间房屋的租金第二年比第一年
多500元,所有房屋出租的租金第一年为9.6万元,第二年为10.2万元.
1.你能找出这一情境中的等量关系吗
2.根据这一情境你能提出哪些问题
3.你能利用方程求出上面提出的问题吗
②第二年每间房屋的租金-第一年每间房屋的租金 =500元
③第一年出租房屋间数 = 第二年出租的房屋间数
①出租房屋间数=
问题1、求出租的房屋总间数;
问题2、分别求这两年每间房屋的租金.
注:先找基础三者关系,再从
这三个量中分别寻找条件.
解决问题
某单位将沿街的一部分房屋出租. 每间房屋的租金第二年比第一年
多500元,所有房屋出租的租金第一年为9.6万元,第二年为10.2万元.
问题1、求出租的房屋总间数;
解:设出租的房屋总间数为x间,
由题意得:
解得 :x=12.
经检验,x=12是原方程的解,且符合题意
答:出租的房屋总间数为12间.
千万不要忘记写检验哟!
解决问题
某单位将沿街的一部分房屋出租. 每间房屋的租金第二年比第一年
多500元,所有房屋出租的租金第一年为9.6万元,第二年为10.2万元.
问题2、分别求这两年每间房屋的租金.
解:设第一年每间房屋的租金为y元,则第二年每间房屋的租金为(y+500)元,根据题意,得
间数 每间房屋的租金 总租金
第一年
第二年
解决问题
某单位将沿街的一部分房屋出租. 每间房屋的租金第二年比第一年
多500元,所有房屋出租的租金第一年为9.6万元,第二年为10.2万元.
问题2、分别求这两年每间房屋的租金.
解:设第一年每间房屋的租金为y元,则第二年每间房屋的租金为(y+500)元,由题意得:
解得: y=8000
经检验,y=8000是原方程的解,且符合题意
y+500=8500.
答:第一年每间房屋的租金为8000元,第二年每间房屋的租金为8500元.
(1)审:审清题意;
(2)找:找出等量关系;
(3)设:设出未知数(直接设法、间接设法);
(5)解:解分式方程;
(7)答:写出答案.
(4)列:用代数式表示等量关系,列出分式方程;
(6)检:必须检验根的正确性与合理性;
归纳
列分式方程解应用题的步骤
验!验!验!
最重要!
巩固练习
1. 小明和同学一起去书店买书,他们先用15元买了一种科普书,又用15元
买了一种文学书. 科普书的价格比文学书高出一半,因此他们所买的科普书
比所买的文学书少1本. 这种科普书和这种文学书的价格各是多少
等量关系:
1.书本数=
2.科普书价格=文学书价格×1.5
3.所买文学书本数-所买的科普书本数=1
解:设文学书的价格是每本x元,则
科普书的价格是每本1.5x元.
由题意得:
解得 : x=5
经检验,x=5是原方程的解,且符合题意.
∴1.5x=1.5×5=7.5
答:文学书的价格是每本5元,
科普书的价格是每本7.5元.
巩固练习
2. 某商店销售一批服装,每件售价350元,可获利25%,求这种服装的成本价.
设这种服装的成本价为x元,则可列方程为( )
A.x=350×25% B.25%×x=350 C. D.350﹣x=25%
3.港珠澳大桥是我国桥梁建筑史上的又一伟大奇迹,东接香港,西接珠海、澳
门,全程55千米.通车前需走水陆两路共约170千米,通车后,约减少时间
3小时,平均速度是原来的2.5倍,如果设原来通车前的平均时速为x千米/小时,
则可列方程为 .
巩固练习
2. 某商店销售一批服装,每件售价150元,可获利25%,求这种服装的成本价.设这种服装的成本价为x元,则得到方程( )
A.x=150×25% B.25%×x=150 C. D.150﹣x=25%
C
利润问题:利润=售价-进价,利润率= ×100%
利润=150-x
分式方程
整式方程
能力提升
4.两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成. 哪个队的施工速度快?
表格法分析:
工作时间(月) 工作效率 工作量
甲队
乙队
等量关系:
甲队完成的工作总量+乙队完成的工作总量=“1”
设乙单独完成这项工程需要x个月.
此时,列方程为:
能力提升
4.两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成. 哪个队的施工速度快?
解:设乙单独完成这项工程需要x个月. 记工作总量为1,甲的工作效率是 ,
由题意得:
化简得:
解得 :x=1.
经检验x=1是原方程的解,且符合题意.
∵乙队单独施工1个月可以完成全部任务,而甲队单独施工需3个月才可以完成全部任务,
∴乙队的施工速度快.
能力提升
4.两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成. 哪个队的施工速度快?
想一想:本题的列方程所用的等量关系还可以怎么找?
甲队单独完成的工作总量+两队合作完成的工作总量=“1”
工作时间 工作效率 工作量
甲单独
两队合作
设乙单独完成这项工程需要x天.
此时,列方程为:
1
课堂小结
实际问题
找等量关系
设未知数、列方程
数学问题
(分式方程)
解方程
方程的解
检验
实际问题
的答案
建模
(1)收费问题:总价=单价×数量
(2)利润问题:利润=售价-进价,利润率= ×100%
(3)行程问题: 路程=速度×时间
(4)工程问题:工作量=工作效率×工作时间
……
基本等量关系
课堂小结
和(差)、倍(分)
当堂检测
利用分式方程解决下列问题:
为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买A种图书花费了3000元,购买B种图书花费了1600元,A种图书的
单价是B种图书的1.5倍,购买A种图书的数量比B种图书多20本.求A和B
两种图书的单价.
解:(1)设B种图书的单价为x元,则A种图书的单价为1.5x元,
由题意得:
解得: x=20,
经检验,x=20是所列方程的解,且符合题意,
∴1.5x=30.
答:A种图书的单价为30元,B种图书的单价为20元.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
