2021-2022学年浙教版七年级数学下册3.4乘法公式-完全平方公式优生辅导训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版七年级数学下册3.4乘法公式-完全平方公式优生辅导训练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 71.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 18:33:46 | ||
图片预览




文档简介
2021-2022学年浙教版七年级数学下册《3-4乘法公式-完全平方公式》
优生辅导训练(附答案)
一.选择题
1.若(x+1)2=x2+mx+1,则m的值是( )
A.1 B.﹣1 C.2 D.﹣2
2.若x+4=2y,则代数式x2﹣4xy+4y2的值为( )
A.6 B.8 C.12 D.16
3.若x2﹣8x+m是完全平方式,则m的值为( )
A.16 B.±16 C.±4 D.4
4.若x2+ax+16是完全平方式,在|a﹣2|的值是( )
A.6 B.6或10 C.2 D.2或6
5.若(y﹣a)2=y2﹣by+,则a的值可能是( )
A. B. C. D.
6.将四个长为a,宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2,若S1=2S2,则a,b满足( )
A.a=2b B.a=3b C.2a=3b D.2a=5b
7.如图,两个正方形的边长分别为a、b,若a+b=7,ab=3,则阴影部分的面积是( )
A.40 B. C.20 D.23
8.已知(m﹣2022)(m﹣2020)=25,则(m﹣2020)2+(m﹣2022)2的值为( )
A.54 B.46 C.2021 D.2022
二.填空题
9.若(x+y)2=8,xy=3,则x2+y2= .
10.如图,两个阴影图形都是正方形,用两种方式表示这两个正方形的面积和,可以得到的等式为 .
11.已知x+y=3,x2+y2=23,(x﹣y)2的值为 .
12.一个正方形的边长增加3cm,它的面积就增加kcm2(k>9),则这个正方形的边长是 cm.(请用含k的式子表示)
13.已知长方形的周长为28,面积为48.则分别以长方形的长和宽为边长的两个正方形的面积和是 .
14.已知m2+n2﹣6m+10n+34=0,则m+n= .
15.如图,两个正方形的边长分别为a,b,若a+b=7,ab=12,则阴影部分的面积为 .
三.解答题
16.化简:m(m﹣2n)﹣(m﹣n)2.
17.已知m+n=3,mn=2.
(1)当a=2时,求am an﹣(am)n的值;
(2)求(m﹣n)2+(m﹣4)(n﹣4)的值.
18.如图,某区有一块长为(3a+4b)米,宽为(2a+3b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间的边长为(a+b)米的空白的正方形地块将修建一个凉亭.
(1)用含有a,b的式子表示绿化总面积.
(2)若a=4,b=3,求出此时的绿化总面积.
19.如图,正方形ABCD的边长为a,点E在AB边上,四边形EFGB也是正方形,它的边长为b(a>b),连接AF、CF、AC.
(1)用含a、b的代数式表示GC= ;
(2)若两个正方形的面积之和为60,即a2+b2=60,又ab=20,图中线段GC的长;
(3)若a=8,△AFC的面积为S,则S= .
20.完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1
所以(a+b)2=9,2ab=2
所以a2+b2+2ab=9,2ab=2
得a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)若x+y=8,x2+y2=40,求xy的值;
(2)①若(4﹣x)x=5,则(4﹣x)2+x2= ;
②若(4﹣x)(5﹣x)=8,则(4﹣x)2+(5﹣x)2= ;
(3)如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=6,两正方形的面积和S1+S2=18,求图中阴影部分面积.
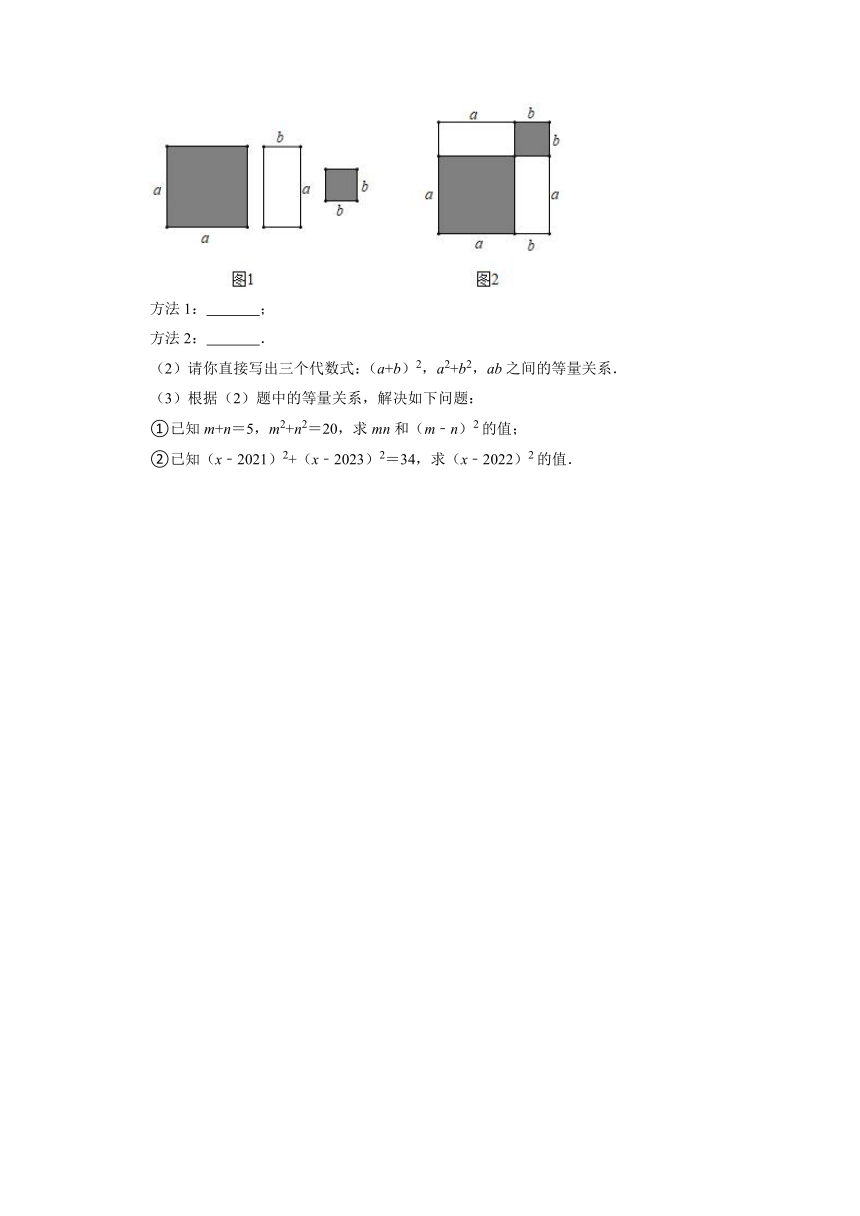
21.数学活动课上,老师准备了图1中三种不同大小的正方形与长方形,拼成了一个如图2所示的正方形.
(1)请用两种不同的方法表示图2中阴影部分的面积和.
方法1: ;
方法2: .
(2)请你直接写出三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知m+n=5,m2+n2=20,求mn和(m﹣n)2的值;
②已知(x﹣2021)2+(x﹣2023)2=34,求(x﹣2022)2的值.
参考答案
一.选择题
1.解:(x+1)2=x2+2x+1,
∵(x+1)2=x2+mx+1,
∴m=2,
故选:C.
2.解:∵x+4=2y,
∴x﹣2y=﹣4,
∴x2﹣4xy+4y2=(x﹣2y)2=(﹣4)2=16.
故选:D.
3.解:∵x2﹣8x+m是完全平方式,
∴m=16.
故选:A.
4.解:∵(x±4)2=x2±8x+16,
∴a=±8,
当a=8时,
|a﹣2|=|6|=6,
当a=﹣8时,
|a﹣2|=|﹣10|=10,
故选:B.
5.解:由完全平方式y2﹣by+,
可得a=±,b=2×(±)=±1,
故选:C.
6.解:∵S1=2×b(a+b)+2×ab+2×(a﹣b)
=a2+2b2,
S2=(a+b)2﹣(a2+2b2)
=2ab﹣b2,
又∵S1=2S2,
∴a2+2b2=2(2ab﹣b2),
整理,得(a﹣2b)2=0,
∴a﹣2b=0,
∴a=2b.
故选:A.
7.解:由题意可得阴影部分的面积为:
a2+b2﹣a2﹣(a+b)b
=a2+b2﹣a2﹣ab﹣b2
=
=,
∴当a+b=7,ab=3时,
原式====20,
故选:C.
8.解:∵(m﹣2022)(m﹣2020)=25,
∴m2﹣4022m+2020×2022=25,
∴m2﹣4022m=25﹣2020×2022,
∴原式=m2﹣4040m+20202+m2﹣4044m+20222
=2m2﹣8084m+20202+20222
=2(m2﹣4042m)+20202+20222
=2(25﹣2020×2022)+20202+20222
=20202﹣2×2020×2022+20222+50
=(2020﹣2022)2+50
=4+50
=54,
故选:A.
二.填空题
9.解:∵(x+y)2=8,
∴x2+2xy+y2=8,
∵xy=3,
∴x2+6+y2=8,
∴x2+y2=2,
故答案为:2.
10.解:①两个阴影部分正方形的面积和为:a2+b2,
②两个阴影部分正方形的面积和为:(a+b)2﹣2ab,
∴可以得到等式a2+b2=(a+b)2﹣2ab,
故答案为:a2+b2=(a+b)2﹣2ab.
11.解:∵x+y=3,x2+y2=23,
∴2xy=(x+y)2﹣(x2+y2)=32﹣23=﹣14,
∴xy=﹣7;
∴(x﹣y)2=(x+y)2﹣4xy=32﹣4×(﹣7)=37.
故答案为:37.
12.解:设该正方形的边长为acm,根据题意得,
(a+3)2﹣a2=k,
去括号得,a2+6a+9﹣a2=k,
移项合并得,6a=k﹣9,
系数化为1,得a=,
故答案为:.
13.解:设长方形的长为a,宽为b,
∴a+b=14,ab=48,
由题可知,两个正方形面积和为a2+b2=(a+b)2﹣2ab=196﹣96=100,
故答案为100.
14.解:根据题意,m2+n2﹣6m+10n+34=0,
变形后:(m﹣3)2+(n+5)2=0;
得m=3,n=﹣5;
所以,m+n=﹣2.
15.解:由完全平方公式(a+b)2=a2+2ab+b2,
可得a2+b2=(a+b)2﹣2ab=72﹣2×12=49﹣24=25,
∴阴影部分的面积为:﹣ b
=
=
=,
故答案为:.
三.解答题
16.解:原式=m2﹣2mn﹣m2+2mn﹣n2=﹣n2.
17.解:(1)∵m+n=3,mn=2,
∴原式=am+n﹣amn
=a3﹣a2,
当a=2时,原式=8﹣4=4;
(2)∵m+n=3,mn=2,
∴(m﹣n)2=(m+n)2﹣4mn=9﹣8=1,
∴原式=1+mn﹣4(m+n)+16
=1+2﹣12+16
=7.
18.解:(1)由题意得:长方形地块的面积=(3a+4b)(2a+3b)=(6a2+17ab+12b2)(平方米),
正方形凉亭的面积为:(a+b)2=(a2+2ab+b2)(平方米),
则绿化面积S=(6a2+17ab+12b2)﹣(a2+2ab+b2)=(5a2+15ab+11b2)(平方米);
(2)∵a=4,b=3,
∴绿化总面积S=5a2+15ab+11b2=5×42+15×4×3+11×32=359(平方米).
19.解:(1)∵GC=GB+BC,
∴GC=a+b
故答案为:a+b
(2)∵(a+b)2=a2+b2+2ab=60+20×2=100
∴a+b=10
∴GC=10
(3)S△AFC=S△AFE+S FGBE+S△ABC﹣S△FGC
=b(a﹣b)+b2+a2﹣b(b+a)
=ab﹣b2+b2+a2﹣b2﹣ab
=a2
=×82
=32
故答案为:32
20.解:(1)∵x+y=8;
∴(x+y)2=82;
x2+2xy+y2=64;
又∵x2+y2=40;
∴2xy=64﹣(x2+y2),
∴2xy=64﹣40=24,
xy=12.
(2)①∵(4﹣x)+x=4,
∴[(4﹣x)+x]2=42
[(4﹣x)+x]2=(4﹣x)2+2(4﹣x)x+x2=16;
又∵(4﹣x)x=5,
∴(4﹣x)2+x2=16﹣2(4﹣x)x=16﹣2×5=6.
②由(4﹣x)﹣(5﹣x)=﹣1,
∴[(4﹣x)﹣(5﹣x)]2=(4﹣x)2﹣2(4﹣x)(5﹣x)+(5﹣x)2=(﹣1)2;
又∵(4﹣x)(5﹣x)=8,
∴(4﹣x)2+(5﹣x)2=1+2(4﹣x)(5﹣x)=1+2×8=17.
(3)由题意可得,AC+BC=6,AC2+BC2=18;
∵(AC+BC)2=62,AC2+2AC BC+BC2=36;
∴2AC BC=36﹣(AC2+BC2)=36﹣18=18,
AC BC=9;
图中阴影部分面积为直角三角形面积,
∵BC=CF
∴.
21.解:(1)阴影两部分求和为a2+b2,用总面积减去空白部分面积为(a+b)2﹣2ab,
故答案为:a2+b2,(a+b)2﹣2ab;
(2)由题意得,a2+b2=(a+b)2﹣2ab;
(3)①由(2)题结论a2+b2=(a+b)2﹣2ab可得ab=,
∴m+n=5,m2+n2=20时,
mn=
=
=,
(m﹣n)2
=m2﹣2mn+n2;
=20﹣2×
=20﹣5
=15;
②设a=x﹣2021,b=x﹣2023,
可得a+b=(x﹣2021)+(x﹣2023)
=x﹣2021+x﹣2023
=2x﹣4044
=2(x﹣2022),
由(2)题结论a2+b2=(a+b)2﹣2ab可得,
(a+b)2=a2+2ab+b2,
又∵(a﹣b)2=[(x﹣2021)﹣(x﹣2023)]2=22=4,
且由(a﹣b)2=a2﹣2ab+b2,可得2ab=(a2+b2)﹣(a﹣b)2=(x﹣2021)2+(x﹣2023)2﹣[(x﹣2021)﹣(x﹣2023)]2=34﹣4=30,
∴(x﹣2022)2=()2====16.
优生辅导训练(附答案)
一.选择题
1.若(x+1)2=x2+mx+1,则m的值是( )
A.1 B.﹣1 C.2 D.﹣2
2.若x+4=2y,则代数式x2﹣4xy+4y2的值为( )
A.6 B.8 C.12 D.16
3.若x2﹣8x+m是完全平方式,则m的值为( )
A.16 B.±16 C.±4 D.4
4.若x2+ax+16是完全平方式,在|a﹣2|的值是( )
A.6 B.6或10 C.2 D.2或6
5.若(y﹣a)2=y2﹣by+,则a的值可能是( )
A. B. C. D.
6.将四个长为a,宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2,若S1=2S2,则a,b满足( )
A.a=2b B.a=3b C.2a=3b D.2a=5b
7.如图,两个正方形的边长分别为a、b,若a+b=7,ab=3,则阴影部分的面积是( )
A.40 B. C.20 D.23
8.已知(m﹣2022)(m﹣2020)=25,则(m﹣2020)2+(m﹣2022)2的值为( )
A.54 B.46 C.2021 D.2022
二.填空题
9.若(x+y)2=8,xy=3,则x2+y2= .
10.如图,两个阴影图形都是正方形,用两种方式表示这两个正方形的面积和,可以得到的等式为 .
11.已知x+y=3,x2+y2=23,(x﹣y)2的值为 .
12.一个正方形的边长增加3cm,它的面积就增加kcm2(k>9),则这个正方形的边长是 cm.(请用含k的式子表示)
13.已知长方形的周长为28,面积为48.则分别以长方形的长和宽为边长的两个正方形的面积和是 .
14.已知m2+n2﹣6m+10n+34=0,则m+n= .
15.如图,两个正方形的边长分别为a,b,若a+b=7,ab=12,则阴影部分的面积为 .
三.解答题
16.化简:m(m﹣2n)﹣(m﹣n)2.
17.已知m+n=3,mn=2.
(1)当a=2时,求am an﹣(am)n的值;
(2)求(m﹣n)2+(m﹣4)(n﹣4)的值.
18.如图,某区有一块长为(3a+4b)米,宽为(2a+3b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间的边长为(a+b)米的空白的正方形地块将修建一个凉亭.
(1)用含有a,b的式子表示绿化总面积.
(2)若a=4,b=3,求出此时的绿化总面积.
19.如图,正方形ABCD的边长为a,点E在AB边上,四边形EFGB也是正方形,它的边长为b(a>b),连接AF、CF、AC.
(1)用含a、b的代数式表示GC= ;
(2)若两个正方形的面积之和为60,即a2+b2=60,又ab=20,图中线段GC的长;
(3)若a=8,△AFC的面积为S,则S= .
20.完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1
所以(a+b)2=9,2ab=2
所以a2+b2+2ab=9,2ab=2
得a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)若x+y=8,x2+y2=40,求xy的值;
(2)①若(4﹣x)x=5,则(4﹣x)2+x2= ;
②若(4﹣x)(5﹣x)=8,则(4﹣x)2+(5﹣x)2= ;
(3)如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=6,两正方形的面积和S1+S2=18,求图中阴影部分面积.
21.数学活动课上,老师准备了图1中三种不同大小的正方形与长方形,拼成了一个如图2所示的正方形.
(1)请用两种不同的方法表示图2中阴影部分的面积和.
方法1: ;
方法2: .
(2)请你直接写出三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知m+n=5,m2+n2=20,求mn和(m﹣n)2的值;
②已知(x﹣2021)2+(x﹣2023)2=34,求(x﹣2022)2的值.
参考答案
一.选择题
1.解:(x+1)2=x2+2x+1,
∵(x+1)2=x2+mx+1,
∴m=2,
故选:C.
2.解:∵x+4=2y,
∴x﹣2y=﹣4,
∴x2﹣4xy+4y2=(x﹣2y)2=(﹣4)2=16.
故选:D.
3.解:∵x2﹣8x+m是完全平方式,
∴m=16.
故选:A.
4.解:∵(x±4)2=x2±8x+16,
∴a=±8,
当a=8时,
|a﹣2|=|6|=6,
当a=﹣8时,
|a﹣2|=|﹣10|=10,
故选:B.
5.解:由完全平方式y2﹣by+,
可得a=±,b=2×(±)=±1,
故选:C.
6.解:∵S1=2×b(a+b)+2×ab+2×(a﹣b)
=a2+2b2,
S2=(a+b)2﹣(a2+2b2)
=2ab﹣b2,
又∵S1=2S2,
∴a2+2b2=2(2ab﹣b2),
整理,得(a﹣2b)2=0,
∴a﹣2b=0,
∴a=2b.
故选:A.
7.解:由题意可得阴影部分的面积为:
a2+b2﹣a2﹣(a+b)b
=a2+b2﹣a2﹣ab﹣b2
=
=,
∴当a+b=7,ab=3时,
原式====20,
故选:C.
8.解:∵(m﹣2022)(m﹣2020)=25,
∴m2﹣4022m+2020×2022=25,
∴m2﹣4022m=25﹣2020×2022,
∴原式=m2﹣4040m+20202+m2﹣4044m+20222
=2m2﹣8084m+20202+20222
=2(m2﹣4042m)+20202+20222
=2(25﹣2020×2022)+20202+20222
=20202﹣2×2020×2022+20222+50
=(2020﹣2022)2+50
=4+50
=54,
故选:A.
二.填空题
9.解:∵(x+y)2=8,
∴x2+2xy+y2=8,
∵xy=3,
∴x2+6+y2=8,
∴x2+y2=2,
故答案为:2.
10.解:①两个阴影部分正方形的面积和为:a2+b2,
②两个阴影部分正方形的面积和为:(a+b)2﹣2ab,
∴可以得到等式a2+b2=(a+b)2﹣2ab,
故答案为:a2+b2=(a+b)2﹣2ab.
11.解:∵x+y=3,x2+y2=23,
∴2xy=(x+y)2﹣(x2+y2)=32﹣23=﹣14,
∴xy=﹣7;
∴(x﹣y)2=(x+y)2﹣4xy=32﹣4×(﹣7)=37.
故答案为:37.
12.解:设该正方形的边长为acm,根据题意得,
(a+3)2﹣a2=k,
去括号得,a2+6a+9﹣a2=k,
移项合并得,6a=k﹣9,
系数化为1,得a=,
故答案为:.
13.解:设长方形的长为a,宽为b,
∴a+b=14,ab=48,
由题可知,两个正方形面积和为a2+b2=(a+b)2﹣2ab=196﹣96=100,
故答案为100.
14.解:根据题意,m2+n2﹣6m+10n+34=0,
变形后:(m﹣3)2+(n+5)2=0;
得m=3,n=﹣5;
所以,m+n=﹣2.
15.解:由完全平方公式(a+b)2=a2+2ab+b2,
可得a2+b2=(a+b)2﹣2ab=72﹣2×12=49﹣24=25,
∴阴影部分的面积为:﹣ b
=
=
=,
故答案为:.
三.解答题
16.解:原式=m2﹣2mn﹣m2+2mn﹣n2=﹣n2.
17.解:(1)∵m+n=3,mn=2,
∴原式=am+n﹣amn
=a3﹣a2,
当a=2时,原式=8﹣4=4;
(2)∵m+n=3,mn=2,
∴(m﹣n)2=(m+n)2﹣4mn=9﹣8=1,
∴原式=1+mn﹣4(m+n)+16
=1+2﹣12+16
=7.
18.解:(1)由题意得:长方形地块的面积=(3a+4b)(2a+3b)=(6a2+17ab+12b2)(平方米),
正方形凉亭的面积为:(a+b)2=(a2+2ab+b2)(平方米),
则绿化面积S=(6a2+17ab+12b2)﹣(a2+2ab+b2)=(5a2+15ab+11b2)(平方米);
(2)∵a=4,b=3,
∴绿化总面积S=5a2+15ab+11b2=5×42+15×4×3+11×32=359(平方米).
19.解:(1)∵GC=GB+BC,
∴GC=a+b
故答案为:a+b
(2)∵(a+b)2=a2+b2+2ab=60+20×2=100
∴a+b=10
∴GC=10
(3)S△AFC=S△AFE+S FGBE+S△ABC﹣S△FGC
=b(a﹣b)+b2+a2﹣b(b+a)
=ab﹣b2+b2+a2﹣b2﹣ab
=a2
=×82
=32
故答案为:32
20.解:(1)∵x+y=8;
∴(x+y)2=82;
x2+2xy+y2=64;
又∵x2+y2=40;
∴2xy=64﹣(x2+y2),
∴2xy=64﹣40=24,
xy=12.
(2)①∵(4﹣x)+x=4,
∴[(4﹣x)+x]2=42
[(4﹣x)+x]2=(4﹣x)2+2(4﹣x)x+x2=16;
又∵(4﹣x)x=5,
∴(4﹣x)2+x2=16﹣2(4﹣x)x=16﹣2×5=6.
②由(4﹣x)﹣(5﹣x)=﹣1,
∴[(4﹣x)﹣(5﹣x)]2=(4﹣x)2﹣2(4﹣x)(5﹣x)+(5﹣x)2=(﹣1)2;
又∵(4﹣x)(5﹣x)=8,
∴(4﹣x)2+(5﹣x)2=1+2(4﹣x)(5﹣x)=1+2×8=17.
(3)由题意可得,AC+BC=6,AC2+BC2=18;
∵(AC+BC)2=62,AC2+2AC BC+BC2=36;
∴2AC BC=36﹣(AC2+BC2)=36﹣18=18,
AC BC=9;
图中阴影部分面积为直角三角形面积,
∵BC=CF
∴.
21.解:(1)阴影两部分求和为a2+b2,用总面积减去空白部分面积为(a+b)2﹣2ab,
故答案为:a2+b2,(a+b)2﹣2ab;
(2)由题意得,a2+b2=(a+b)2﹣2ab;
(3)①由(2)题结论a2+b2=(a+b)2﹣2ab可得ab=,
∴m+n=5,m2+n2=20时,
mn=
=
=,
(m﹣n)2
=m2﹣2mn+n2;
=20﹣2×
=20﹣5
=15;
②设a=x﹣2021,b=x﹣2023,
可得a+b=(x﹣2021)+(x﹣2023)
=x﹣2021+x﹣2023
=2x﹣4044
=2(x﹣2022),
由(2)题结论a2+b2=(a+b)2﹣2ab可得,
(a+b)2=a2+2ab+b2,
又∵(a﹣b)2=[(x﹣2021)﹣(x﹣2023)]2=22=4,
且由(a﹣b)2=a2﹣2ab+b2,可得2ab=(a2+b2)﹣(a﹣b)2=(x﹣2021)2+(x﹣2023)2﹣[(x﹣2021)﹣(x﹣2023)]2=34﹣4=30,
∴(x﹣2022)2=()2====16.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
