3.4 乘法公式 同步练习(含解析)
文档属性
| 名称 | 3.4 乘法公式 同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1003.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 06:08:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版七年级下 3.4乘法公式同步练习
一.选择题
1.(2020 雁塔区校级模拟)下列计算正确的是( )
A.2a3 3a3=6a9 B.(a4b)2=a6b2
C.6a4b3÷3a2b3=2a2 D.(a+2)(a﹣2)=a2﹣2
2.(2021秋 武威月考)下列式子可用平方差公式计算的是( )
A.(a+b)(﹣a﹣b) B.(a﹣b)(b﹣a)
C.(a+2b)(2b+a) D.(y﹣2x)(2x+y)
3.(2022春 杏花岭区校级月考)计算2022﹣201×203的结果是( )
A.1 B.﹣1 C.2 D.﹣2
4.(2021秋 硚口区期末)计算(x+2y﹣3)(x﹣2y+3)的结果是( )
A.x2﹣4y2+12y﹣9 B.﹣x2+4y2﹣12y+9
C.x2﹣4y2+9 D.x2﹣4y2﹣12y﹣9
5.(2021秋 普兰店区期末)已知(m+n)2=18,(m﹣n)2=2,那么m2+n2=( )
A.20 B.10 C.16 D.8
6.(2021秋 望城区期末)如果4x2+2kx+25是一个完全平方式,那么k的值是( )
A.20 B.±20 C.10 D.±10
7.(2021秋 船山区校级期末)利用乘法公式计算正确的是( )
A.(4x﹣3)2=8x2+12x﹣9 B.(2m+5)(2m﹣5)=4m2﹣5
C.(a+b)(a+b)=a2+b2 D.(4x+1)2=16x2+8x+1
8.(2021春 博山区期末)如图1,将一个大长方形沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示图形,正好是边长为x的大正方形剪去一个边长为1的小正方形(阴影部分).这两个图能解释下列哪个等式( )
A.(x﹣1)2=x2﹣2x+1 B.(x+1)(x﹣1)=x2﹣1
C.(x+1)2=x2+2x+1 D.x(x﹣1)=x2﹣x
9.(2022 鼓楼区校级开学)已知:(2021﹣a)(2020﹣a)=3,则(2021﹣a)2+(2020﹣a)2的值为( )
A.7 B.8 C.9 D.12
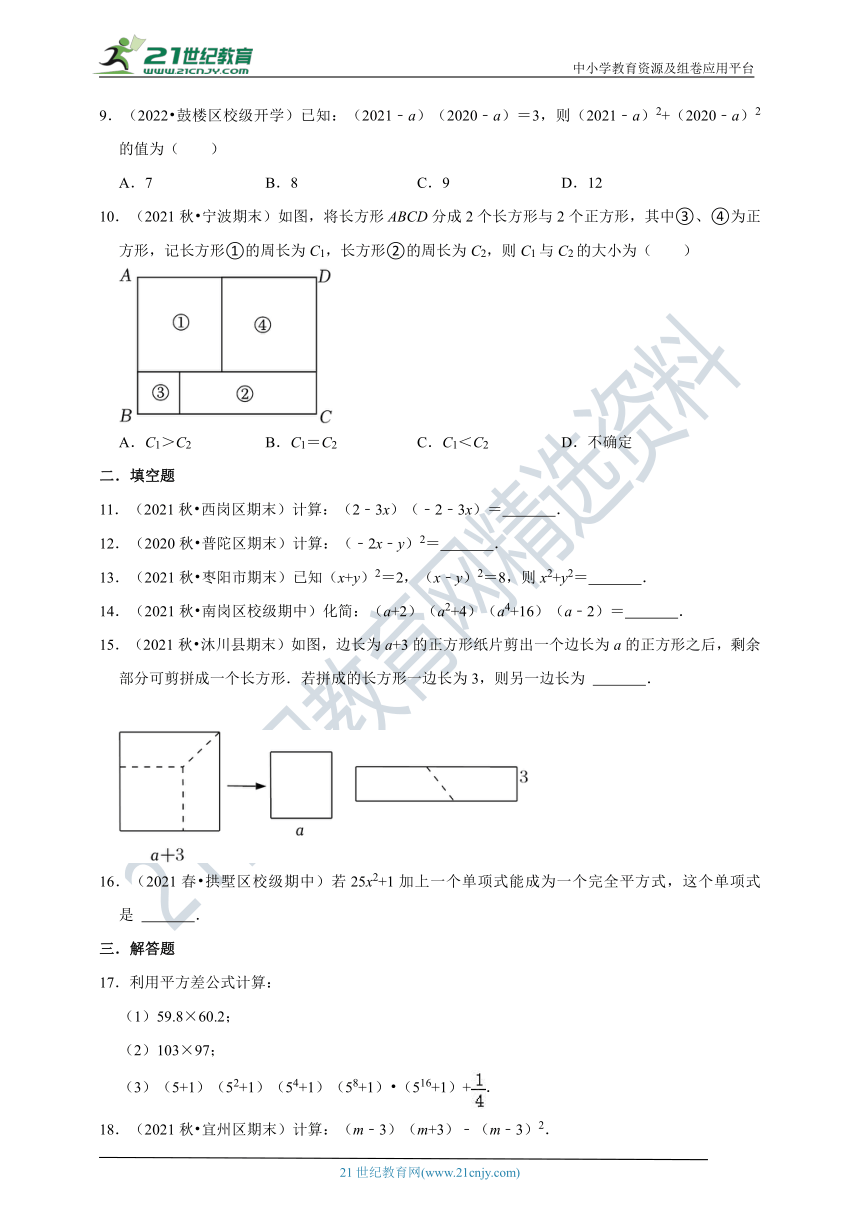
10.(2021秋 宁波期末)如图,将长方形ABCD分成2个长方形与2个正方形,其中③、④为正方形,记长方形①的周长为C1,长方形②的周长为C2,则C1与C2的大小为( )
A.C1>C2 B.C1=C2 C.C1<C2 D.不确定
二.填空题
11.(2021秋 西岗区期末)计算:(2﹣3x)(﹣2﹣3x)= .
12.(2020秋 普陀区期末)计算:(﹣2x﹣y)2= .
13.(2021秋 枣阳市期末)已知(x+y)2=2,(x﹣y)2=8,则x2+y2= .
14.(2021秋 南岗区校级期中)化简:(a+2)(a2+4)(a4+16)(a﹣2)= .
15.(2021秋 沐川县期末)如图,边长为a+3的正方形纸片剪出一个边长为a的正方形之后,剩余部分可剪拼成一个长方形.若拼成的长方形一边长为3,则另一边长为 .
16.(2021春 拱墅区校级期中)若25x2+1加上一个单项式能成为一个完全平方式,这个单项式是 .
三.解答题
17.利用平方差公式计算:
(1)59.8×60.2;
(2)103×97;
(3)(5+1)(52+1)(54+1)(58+1) (516+1)+.
18.(2021秋 宜州区期末)计算:(m﹣3)(m+3)﹣(m﹣3)2.
19.(2021秋 龙山县期末)计算:(3x﹣5)2﹣(2x+7)2.
20.(2021秋 丰台区期末)计算:(2x﹣3)2﹣(x﹣3)(2x+1).
21.(2021秋 自贡期末)计算:x(2﹣x)+(x+2y)(x﹣2y).
22.(2021秋 庐江县期末)化简:(3m+n)2﹣3m(m+2n).
23.计算题:
(1)(a﹣2b﹣3c)2;
(2)(x+2y﹣z)(x﹣2y﹣z)﹣(x+y﹣z)2.
24.(2021秋 长沙期末)已知(a+b)2=11,ab=1.
(1)求a2+b2的值;
(2)求a﹣b的值.
25.(2021秋 江陵县期末)如图1是一个长为2a、宽为2b的长方形(a>b>0),沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
(1)图2中的阴影部分正方形的边长为 ;
(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若x﹣y=4,xy=2.25,求x+y的值.
答案与解析
一.选择题
1.(2020 雁塔区校级模拟)下列计算正确的是( )
A.2a3 3a3=6a9 B.(a4b)2=a6b2
C.6a4b3÷3a2b3=2a2 D.(a+2)(a﹣2)=a2﹣2
【解析】解:A.2a3 3a3=6a6,故本选项不合题意;
B.(a4b)2=a8b2,故本选项不合题意;
C.6a4b3÷3a2b3=2a2,故本选项符合题意;
D.(a+2)(a﹣2)=a2﹣4,故本选项不合题意.
故选:C.
2.(2021秋 武威月考)下列式子可用平方差公式计算的是( )
A.(a+b)(﹣a﹣b) B.(a﹣b)(b﹣a)
C.(a+2b)(2b+a) D.(y﹣2x)(2x+y)
【解析】解:A:原式=﹣(a+b)2用完全平方公式,∴不符合题意;
B:原式=﹣(a﹣b)2用完全平方公式,∴不符合题意;
C:原式=(a+2b)2用完全平方公式,∴不符合题意;
D:原式=y2﹣4x2用平方差公式,∴符合题意;
故选:D.
3.(2022春 杏花岭区校级月考)计算2022﹣201×203的结果是( )
A.1 B.﹣1 C.2 D.﹣2
【解析】解:2022﹣201×203
=2022﹣(202﹣1)×(202+1)
=2022﹣2022+1
=1.
故选:A.
4.(2021秋 硚口区期末)计算(x+2y﹣3)(x﹣2y+3)的结果是( )
A.x2﹣4y2+12y﹣9 B.﹣x2+4y2﹣12y+9
C.x2﹣4y2+9 D.x2﹣4y2﹣12y﹣9
【解析】解:原式=[x+(2y﹣3)][x﹣(2y﹣3)]
=x2﹣(2y﹣3)2
=x2﹣4y2+12y﹣9,
故选:A.
5.(2021秋 普兰店区期末)已知(m+n)2=18,(m﹣n)2=2,那么m2+n2=( )
A.20 B.10 C.16 D.8
【解析】解:已知等式化简得:
(m+n)2=m2+n2+2mn=18①,
(m﹣n)2=m2+n2﹣2mn=2②,
由①+②得:2(m2+n2)=20,
则m2+n2=10.
故选:B.
6.(2021秋 望城区期末)如果4x2+2kx+25是一个完全平方式,那么k的值是( )
A.20 B.±20 C.10 D.±10
【解析】解:∵4x2+2kx+25=(2x±5)2,
∴2kx=±2×2x 5=±20x,
∴k=±10,
故选:D.
7.(2021秋 船山区校级期末)利用乘法公式计算正确的是( )
A.(4x﹣3)2=8x2+12x﹣9 B.(2m+5)(2m﹣5)=4m2﹣5
C.(a+b)(a+b)=a2+b2 D.(4x+1)2=16x2+8x+1
【解析】解:A.(4x﹣3)2=16x2﹣24x+9,故本选项不合题意;
B.(2m+5)(2m﹣5)=4m2﹣25,故本选项不合题意;
C.(a+b)(a+b)=a2+2ab+b2,故本选项不合题意;
D.(4x+1)2=16x2+8x+1,故本选项符合题意;
故选:D.
8.(2021春 博山区期末)如图1,将一个大长方形沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示图形,正好是边长为x的大正方形剪去一个边长为1的小正方形(阴影部分).这两个图能解释下列哪个等式( )
A.(x﹣1)2=x2﹣2x+1 B.(x+1)(x﹣1)=x2﹣1
C.(x+1)2=x2+2x+1 D.x(x﹣1)=x2﹣x
【解析】解:图1的面积为:(x+1)(x﹣1),
图2中白色部分的面积为:x2﹣1,
∴(x+1)(x﹣1)=x2﹣1,
故选:B.
9.(2022 鼓楼区校级开学)已知:(2021﹣a)(2020﹣a)=3,则(2021﹣a)2+(2020﹣a)2的值为( )
A.7 B.8 C.9 D.12
【解析】解:设x=2021﹣a,y=2020﹣a,
∴x﹣y=2021﹣a﹣2020+a=1,
∵(2021﹣a)(2020﹣a)=3,
∴xy=3,
∴原式=x2+y2
=(x﹣y)2+2xy
=1+2×3
=7,
故选:A.
10.(2021秋 宁波期末)如图,将长方形ABCD分成2个长方形与2个正方形,其中③、④为正方形,记长方形①的周长为C1,长方形②的周长为C2,则C1与C2的大小为( )
A.C1>C2 B.C1=C2 C.C1<C2 D.不确定
【解析】解:如图,设MN=a,NP=b,PQ=m,即正方形③的边长为a,正方形④的边长m,
所以长方形①的长为a+b,宽为m,因此周长C1=(a+b+m)×2=2a+2b+2m,
长方形②的长为m+b,宽为a,因此周长C2=(m+b+a)×2=2a+2b+2m,
所以C1=C2,
故选:B.
二.填空题
11.(2021秋 西岗区期末)计算:(2﹣3x)(﹣2﹣3x)= ﹣4+9x2 .
【解析】解:(2﹣3x)(﹣2﹣3x)=﹣(2﹣3x)(2+3x)=﹣[22﹣(3x)2]=﹣4+9x2.
故答案为:﹣4+9x2.
12.(2020秋 普陀区期末)计算:(﹣2x﹣y)2= 4x2+4xy+y2 .
【解析】解:原式=[﹣(2x+y)]2
=(2x+y)2
=4x2+4xy+y2,
故答案为:4x2+4xy+y2.
13.(2021秋 枣阳市期末)已知(x+y)2=2,(x﹣y)2=8,则x2+y2= 5 .
【解析】解:∵(x+y)2=2,(x﹣y)2=8,
∴x2+2xy+y2=2①,x2﹣2xy+y2=8②,
①+②得:2(x2+y2)=10,
∴x2+y2=5.
故答案为:5.
14.(2021秋 南岗区校级期中)化简:(a+2)(a2+4)(a4+16)(a﹣2)= a8﹣256 .
【解析】解:(a+2)(a2+4)(a4+16)(a﹣2)
=(a+2)(a﹣2)(a2+4)(a4+16)
=(a2﹣4)(a2+4)(a4+16)
=(a4﹣16)(a4+16)
=a8﹣256.
故答案为:a8﹣256.
15.(2021秋 沐川县期末)如图,边长为a+3的正方形纸片剪出一个边长为a的正方形之后,剩余部分可剪拼成一个长方形.若拼成的长方形一边长为3,则另一边长为 2a+3 .
【解析】解:如图,将剩余部分拼成一个长方形.这个长方形一边长为3,另一边长为a+(a+3),
即2a+3,
故答案为:2a+3.
16.(2021春 拱墅区校级期中)若25x2+1加上一个单项式能成为一个完全平方式,这个单项式是 10x或﹣10x或﹣1或﹣25x2或 .
【解析】解:①25x2是平方项时,25x2±10x+1=(5x±1)2,
∴可添加的项是10x或﹣10x,
②25x2是乘积二倍项时,+25x2+1=,
∴可添加的项是,
③可添加﹣1或﹣25x2,
综上所述可添加的项是:10x或﹣10x或﹣1或﹣25x2或.
故答案为:10x或﹣10x或﹣1或﹣25x2或.
三.解答题
17.利用平方差公式计算:
(1)59.8×60.2;
(2)103×97;
(3)(5+1)(52+1)(54+1)(58+1) (516+1)+.
【解析】解:(1)59.8×60.2=(60﹣0.2)(60+0.2)=3600﹣0.04=3599.96;
(2)103×97=(100+3)(100﹣3)=10000﹣9=9991;
(3)(5+1)(52+1)(54+1)(58+1) (516+1)+
=(5﹣1)(5+1)(52+1)(54+1)(58+1) (516+1)+
=(52﹣1)(52+1)(54+1)(58+1) (516+1)+
=(532﹣1)+
=×532
=.
18.(2021秋 宜州区期末)计算:(m﹣3)(m+3)﹣(m﹣3)2.
【解析】解:原式=m2﹣9﹣(m2﹣6m+9)
=m2﹣9﹣m2+6m﹣9
=6m﹣18.
19.(2021秋 龙山县期末)计算:(3x﹣5)2﹣(2x+7)2.
【解析】解:(3x﹣5)2﹣(2x+7)2
=(3x﹣5+2x+7)(3x﹣5﹣2x﹣7)
=(5x+2)(x﹣12)
=5x2﹣60x+2x﹣24
=5x2﹣58x﹣24.
20.(2021秋 丰台区期末)计算:(2x﹣3)2﹣(x﹣3)(2x+1).
【解析】解:原式=4x2﹣12x+9﹣2x2﹣x+6x+3
=2x2﹣7x+12.
21.(2021秋 自贡期末)计算:x(2﹣x)+(x+2y)(x﹣2y).
【解析】解:x(2﹣x)+(x+2y)(x﹣2y)
=2x﹣x2+x2﹣4y2
=2x﹣4y2.
22.(2021秋 庐江县期末)化简:(3m+n)2﹣3m(m+2n).
【解析】解:原式=(9m2+6mn+n2)﹣(3m2+6mn)
=9m2+6mn+n2﹣3m2﹣6mn
=6m2+n2.
23.计算题:
(1)(a﹣2b﹣3c)2;
(2)(x+2y﹣z)(x﹣2y﹣z)﹣(x+y﹣z)2.
【解析】解:(1)原式=(a﹣2b)2﹣2×(a﹣2b)×3c+9c2
=a2+4b2﹣4ab﹣6ac+12bc+9c2
=a2+4b2+9c2﹣4ab﹣6ac+12bc;
(2)原式=[(x﹣z)+2y][(x﹣z)﹣2y]﹣[(x﹣z)+y]2
=(x﹣z)2﹣4y2﹣(x﹣z)2﹣2(x﹣z)y﹣y2
=﹣5y2﹣2xy+2yz.
24.(2021秋 长沙期末)已知(a+b)2=11,ab=1.
(1)求a2+b2的值;
(2)求a﹣b的值.
【解析】解:(1)a2+b2
=(a+b)2﹣2ab
=11﹣2
=9;
(2)∵(a﹣b)2
=a2+b2﹣2ab
=9﹣2
=7,
∴a﹣b=.
25.(2021秋 江陵县期末)如图1是一个长为2a、宽为2b的长方形(a>b>0),沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
(1)图2中的阴影部分正方形的边长为 a﹣b ;
(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 (a+b)2=(a﹣b)2+4ab ;
(3)根据(2)中的结论,若x﹣y=4,xy=2.25,求x+y的值.
【解析】解:(1)由拼图可知,阴影正方形的边长为a﹣b,
故答案为:a﹣b;
(2)大正方形的边长为a+b,因此面积为(a+b)2,阴影小正方形的边长为a﹣b,因此面积为(a﹣b)2,而每个长方形的面积为ab,
由S大正方形=S小正方形+4S长方形可得,
(a+b)2=(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab;
(3)由(2)得,(x+y)2=(x﹣y)2+4xy,
即(x+y)2=42+4×2.25=26,
∴x+y=±.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版七年级下 3.4乘法公式同步练习
一.选择题
1.(2020 雁塔区校级模拟)下列计算正确的是( )
A.2a3 3a3=6a9 B.(a4b)2=a6b2
C.6a4b3÷3a2b3=2a2 D.(a+2)(a﹣2)=a2﹣2
2.(2021秋 武威月考)下列式子可用平方差公式计算的是( )
A.(a+b)(﹣a﹣b) B.(a﹣b)(b﹣a)
C.(a+2b)(2b+a) D.(y﹣2x)(2x+y)
3.(2022春 杏花岭区校级月考)计算2022﹣201×203的结果是( )
A.1 B.﹣1 C.2 D.﹣2
4.(2021秋 硚口区期末)计算(x+2y﹣3)(x﹣2y+3)的结果是( )
A.x2﹣4y2+12y﹣9 B.﹣x2+4y2﹣12y+9
C.x2﹣4y2+9 D.x2﹣4y2﹣12y﹣9
5.(2021秋 普兰店区期末)已知(m+n)2=18,(m﹣n)2=2,那么m2+n2=( )
A.20 B.10 C.16 D.8
6.(2021秋 望城区期末)如果4x2+2kx+25是一个完全平方式,那么k的值是( )
A.20 B.±20 C.10 D.±10
7.(2021秋 船山区校级期末)利用乘法公式计算正确的是( )
A.(4x﹣3)2=8x2+12x﹣9 B.(2m+5)(2m﹣5)=4m2﹣5
C.(a+b)(a+b)=a2+b2 D.(4x+1)2=16x2+8x+1
8.(2021春 博山区期末)如图1,将一个大长方形沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示图形,正好是边长为x的大正方形剪去一个边长为1的小正方形(阴影部分).这两个图能解释下列哪个等式( )
A.(x﹣1)2=x2﹣2x+1 B.(x+1)(x﹣1)=x2﹣1
C.(x+1)2=x2+2x+1 D.x(x﹣1)=x2﹣x
9.(2022 鼓楼区校级开学)已知:(2021﹣a)(2020﹣a)=3,则(2021﹣a)2+(2020﹣a)2的值为( )
A.7 B.8 C.9 D.12
10.(2021秋 宁波期末)如图,将长方形ABCD分成2个长方形与2个正方形,其中③、④为正方形,记长方形①的周长为C1,长方形②的周长为C2,则C1与C2的大小为( )
A.C1>C2 B.C1=C2 C.C1<C2 D.不确定
二.填空题
11.(2021秋 西岗区期末)计算:(2﹣3x)(﹣2﹣3x)= .
12.(2020秋 普陀区期末)计算:(﹣2x﹣y)2= .
13.(2021秋 枣阳市期末)已知(x+y)2=2,(x﹣y)2=8,则x2+y2= .
14.(2021秋 南岗区校级期中)化简:(a+2)(a2+4)(a4+16)(a﹣2)= .
15.(2021秋 沐川县期末)如图,边长为a+3的正方形纸片剪出一个边长为a的正方形之后,剩余部分可剪拼成一个长方形.若拼成的长方形一边长为3,则另一边长为 .
16.(2021春 拱墅区校级期中)若25x2+1加上一个单项式能成为一个完全平方式,这个单项式是 .
三.解答题
17.利用平方差公式计算:
(1)59.8×60.2;
(2)103×97;
(3)(5+1)(52+1)(54+1)(58+1) (516+1)+.
18.(2021秋 宜州区期末)计算:(m﹣3)(m+3)﹣(m﹣3)2.
19.(2021秋 龙山县期末)计算:(3x﹣5)2﹣(2x+7)2.
20.(2021秋 丰台区期末)计算:(2x﹣3)2﹣(x﹣3)(2x+1).
21.(2021秋 自贡期末)计算:x(2﹣x)+(x+2y)(x﹣2y).
22.(2021秋 庐江县期末)化简:(3m+n)2﹣3m(m+2n).
23.计算题:
(1)(a﹣2b﹣3c)2;
(2)(x+2y﹣z)(x﹣2y﹣z)﹣(x+y﹣z)2.
24.(2021秋 长沙期末)已知(a+b)2=11,ab=1.
(1)求a2+b2的值;
(2)求a﹣b的值.
25.(2021秋 江陵县期末)如图1是一个长为2a、宽为2b的长方形(a>b>0),沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
(1)图2中的阴影部分正方形的边长为 ;
(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若x﹣y=4,xy=2.25,求x+y的值.
答案与解析
一.选择题
1.(2020 雁塔区校级模拟)下列计算正确的是( )
A.2a3 3a3=6a9 B.(a4b)2=a6b2
C.6a4b3÷3a2b3=2a2 D.(a+2)(a﹣2)=a2﹣2
【解析】解:A.2a3 3a3=6a6,故本选项不合题意;
B.(a4b)2=a8b2,故本选项不合题意;
C.6a4b3÷3a2b3=2a2,故本选项符合题意;
D.(a+2)(a﹣2)=a2﹣4,故本选项不合题意.
故选:C.
2.(2021秋 武威月考)下列式子可用平方差公式计算的是( )
A.(a+b)(﹣a﹣b) B.(a﹣b)(b﹣a)
C.(a+2b)(2b+a) D.(y﹣2x)(2x+y)
【解析】解:A:原式=﹣(a+b)2用完全平方公式,∴不符合题意;
B:原式=﹣(a﹣b)2用完全平方公式,∴不符合题意;
C:原式=(a+2b)2用完全平方公式,∴不符合题意;
D:原式=y2﹣4x2用平方差公式,∴符合题意;
故选:D.
3.(2022春 杏花岭区校级月考)计算2022﹣201×203的结果是( )
A.1 B.﹣1 C.2 D.﹣2
【解析】解:2022﹣201×203
=2022﹣(202﹣1)×(202+1)
=2022﹣2022+1
=1.
故选:A.
4.(2021秋 硚口区期末)计算(x+2y﹣3)(x﹣2y+3)的结果是( )
A.x2﹣4y2+12y﹣9 B.﹣x2+4y2﹣12y+9
C.x2﹣4y2+9 D.x2﹣4y2﹣12y﹣9
【解析】解:原式=[x+(2y﹣3)][x﹣(2y﹣3)]
=x2﹣(2y﹣3)2
=x2﹣4y2+12y﹣9,
故选:A.
5.(2021秋 普兰店区期末)已知(m+n)2=18,(m﹣n)2=2,那么m2+n2=( )
A.20 B.10 C.16 D.8
【解析】解:已知等式化简得:
(m+n)2=m2+n2+2mn=18①,
(m﹣n)2=m2+n2﹣2mn=2②,
由①+②得:2(m2+n2)=20,
则m2+n2=10.
故选:B.
6.(2021秋 望城区期末)如果4x2+2kx+25是一个完全平方式,那么k的值是( )
A.20 B.±20 C.10 D.±10
【解析】解:∵4x2+2kx+25=(2x±5)2,
∴2kx=±2×2x 5=±20x,
∴k=±10,
故选:D.
7.(2021秋 船山区校级期末)利用乘法公式计算正确的是( )
A.(4x﹣3)2=8x2+12x﹣9 B.(2m+5)(2m﹣5)=4m2﹣5
C.(a+b)(a+b)=a2+b2 D.(4x+1)2=16x2+8x+1
【解析】解:A.(4x﹣3)2=16x2﹣24x+9,故本选项不合题意;
B.(2m+5)(2m﹣5)=4m2﹣25,故本选项不合题意;
C.(a+b)(a+b)=a2+2ab+b2,故本选项不合题意;
D.(4x+1)2=16x2+8x+1,故本选项符合题意;
故选:D.
8.(2021春 博山区期末)如图1,将一个大长方形沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示图形,正好是边长为x的大正方形剪去一个边长为1的小正方形(阴影部分).这两个图能解释下列哪个等式( )
A.(x﹣1)2=x2﹣2x+1 B.(x+1)(x﹣1)=x2﹣1
C.(x+1)2=x2+2x+1 D.x(x﹣1)=x2﹣x
【解析】解:图1的面积为:(x+1)(x﹣1),
图2中白色部分的面积为:x2﹣1,
∴(x+1)(x﹣1)=x2﹣1,
故选:B.
9.(2022 鼓楼区校级开学)已知:(2021﹣a)(2020﹣a)=3,则(2021﹣a)2+(2020﹣a)2的值为( )
A.7 B.8 C.9 D.12
【解析】解:设x=2021﹣a,y=2020﹣a,
∴x﹣y=2021﹣a﹣2020+a=1,
∵(2021﹣a)(2020﹣a)=3,
∴xy=3,
∴原式=x2+y2
=(x﹣y)2+2xy
=1+2×3
=7,
故选:A.
10.(2021秋 宁波期末)如图,将长方形ABCD分成2个长方形与2个正方形,其中③、④为正方形,记长方形①的周长为C1,长方形②的周长为C2,则C1与C2的大小为( )
A.C1>C2 B.C1=C2 C.C1<C2 D.不确定
【解析】解:如图,设MN=a,NP=b,PQ=m,即正方形③的边长为a,正方形④的边长m,
所以长方形①的长为a+b,宽为m,因此周长C1=(a+b+m)×2=2a+2b+2m,
长方形②的长为m+b,宽为a,因此周长C2=(m+b+a)×2=2a+2b+2m,
所以C1=C2,
故选:B.
二.填空题
11.(2021秋 西岗区期末)计算:(2﹣3x)(﹣2﹣3x)= ﹣4+9x2 .
【解析】解:(2﹣3x)(﹣2﹣3x)=﹣(2﹣3x)(2+3x)=﹣[22﹣(3x)2]=﹣4+9x2.
故答案为:﹣4+9x2.
12.(2020秋 普陀区期末)计算:(﹣2x﹣y)2= 4x2+4xy+y2 .
【解析】解:原式=[﹣(2x+y)]2
=(2x+y)2
=4x2+4xy+y2,
故答案为:4x2+4xy+y2.
13.(2021秋 枣阳市期末)已知(x+y)2=2,(x﹣y)2=8,则x2+y2= 5 .
【解析】解:∵(x+y)2=2,(x﹣y)2=8,
∴x2+2xy+y2=2①,x2﹣2xy+y2=8②,
①+②得:2(x2+y2)=10,
∴x2+y2=5.
故答案为:5.
14.(2021秋 南岗区校级期中)化简:(a+2)(a2+4)(a4+16)(a﹣2)= a8﹣256 .
【解析】解:(a+2)(a2+4)(a4+16)(a﹣2)
=(a+2)(a﹣2)(a2+4)(a4+16)
=(a2﹣4)(a2+4)(a4+16)
=(a4﹣16)(a4+16)
=a8﹣256.
故答案为:a8﹣256.
15.(2021秋 沐川县期末)如图,边长为a+3的正方形纸片剪出一个边长为a的正方形之后,剩余部分可剪拼成一个长方形.若拼成的长方形一边长为3,则另一边长为 2a+3 .
【解析】解:如图,将剩余部分拼成一个长方形.这个长方形一边长为3,另一边长为a+(a+3),
即2a+3,
故答案为:2a+3.
16.(2021春 拱墅区校级期中)若25x2+1加上一个单项式能成为一个完全平方式,这个单项式是 10x或﹣10x或﹣1或﹣25x2或 .
【解析】解:①25x2是平方项时,25x2±10x+1=(5x±1)2,
∴可添加的项是10x或﹣10x,
②25x2是乘积二倍项时,+25x2+1=,
∴可添加的项是,
③可添加﹣1或﹣25x2,
综上所述可添加的项是:10x或﹣10x或﹣1或﹣25x2或.
故答案为:10x或﹣10x或﹣1或﹣25x2或.
三.解答题
17.利用平方差公式计算:
(1)59.8×60.2;
(2)103×97;
(3)(5+1)(52+1)(54+1)(58+1) (516+1)+.
【解析】解:(1)59.8×60.2=(60﹣0.2)(60+0.2)=3600﹣0.04=3599.96;
(2)103×97=(100+3)(100﹣3)=10000﹣9=9991;
(3)(5+1)(52+1)(54+1)(58+1) (516+1)+
=(5﹣1)(5+1)(52+1)(54+1)(58+1) (516+1)+
=(52﹣1)(52+1)(54+1)(58+1) (516+1)+
=(532﹣1)+
=×532
=.
18.(2021秋 宜州区期末)计算:(m﹣3)(m+3)﹣(m﹣3)2.
【解析】解:原式=m2﹣9﹣(m2﹣6m+9)
=m2﹣9﹣m2+6m﹣9
=6m﹣18.
19.(2021秋 龙山县期末)计算:(3x﹣5)2﹣(2x+7)2.
【解析】解:(3x﹣5)2﹣(2x+7)2
=(3x﹣5+2x+7)(3x﹣5﹣2x﹣7)
=(5x+2)(x﹣12)
=5x2﹣60x+2x﹣24
=5x2﹣58x﹣24.
20.(2021秋 丰台区期末)计算:(2x﹣3)2﹣(x﹣3)(2x+1).
【解析】解:原式=4x2﹣12x+9﹣2x2﹣x+6x+3
=2x2﹣7x+12.
21.(2021秋 自贡期末)计算:x(2﹣x)+(x+2y)(x﹣2y).
【解析】解:x(2﹣x)+(x+2y)(x﹣2y)
=2x﹣x2+x2﹣4y2
=2x﹣4y2.
22.(2021秋 庐江县期末)化简:(3m+n)2﹣3m(m+2n).
【解析】解:原式=(9m2+6mn+n2)﹣(3m2+6mn)
=9m2+6mn+n2﹣3m2﹣6mn
=6m2+n2.
23.计算题:
(1)(a﹣2b﹣3c)2;
(2)(x+2y﹣z)(x﹣2y﹣z)﹣(x+y﹣z)2.
【解析】解:(1)原式=(a﹣2b)2﹣2×(a﹣2b)×3c+9c2
=a2+4b2﹣4ab﹣6ac+12bc+9c2
=a2+4b2+9c2﹣4ab﹣6ac+12bc;
(2)原式=[(x﹣z)+2y][(x﹣z)﹣2y]﹣[(x﹣z)+y]2
=(x﹣z)2﹣4y2﹣(x﹣z)2﹣2(x﹣z)y﹣y2
=﹣5y2﹣2xy+2yz.
24.(2021秋 长沙期末)已知(a+b)2=11,ab=1.
(1)求a2+b2的值;
(2)求a﹣b的值.
【解析】解:(1)a2+b2
=(a+b)2﹣2ab
=11﹣2
=9;
(2)∵(a﹣b)2
=a2+b2﹣2ab
=9﹣2
=7,
∴a﹣b=.
25.(2021秋 江陵县期末)如图1是一个长为2a、宽为2b的长方形(a>b>0),沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
(1)图2中的阴影部分正方形的边长为 a﹣b ;
(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 (a+b)2=(a﹣b)2+4ab ;
(3)根据(2)中的结论,若x﹣y=4,xy=2.25,求x+y的值.
【解析】解:(1)由拼图可知,阴影正方形的边长为a﹣b,
故答案为:a﹣b;
(2)大正方形的边长为a+b,因此面积为(a+b)2,阴影小正方形的边长为a﹣b,因此面积为(a﹣b)2,而每个长方形的面积为ab,
由S大正方形=S小正方形+4S长方形可得,
(a+b)2=(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab;
(3)由(2)得,(x+y)2=(x﹣y)2+4xy,
即(x+y)2=42+4×2.25=26,
∴x+y=±.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
