3.4乘法公式(1)-平方差公式 课件(共18张PPT)
文档属性
| 名称 | 3.4乘法公式(1)-平方差公式 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 13:50:40 | ||
图片预览





文档简介
(共18张PPT)
3.4乘法公式(1)
—平方差公式
浙教版 七年级下册
根据所学知识,计算下列多项式的积,你能发现什么规律? (1)(x+5)(x-5) = ;
(2)(3x+y)(3x-y)= ;
(3)(3m+2n)(3m–2n)= .
9 –
9 –
相乘的两个多项式的各项与它们的积中的各项有什么关系?
新知导入
你能证明(a+b)(a-b)=a2-b2吗?
方法1:利用多项式的乘法法则验证:
(a+b)(a-b)
=a2-ab+ab-b2
= a2-b2
新知讲解
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)=a2-b2
a-b
a-b
(a+b)(a-b)
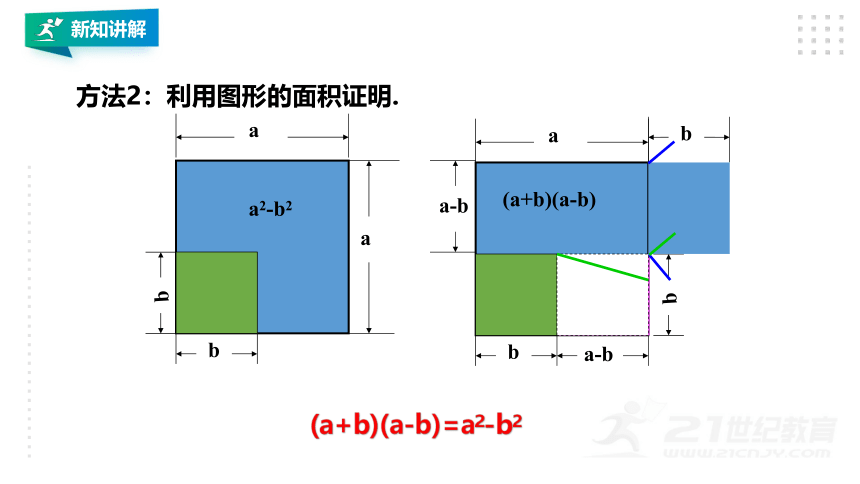
方法2:利用图形的面积证明.
新知讲解
(a+b)(a-b)=a2-b2.
两数和与这两数差的积等于这两数的平方差.
平方差公式
代数推导:
文字描述:两个数的和与这两个数差的积,等于这两个数的平方差.
结构特点:
左边:a符号相同,b符号相反.
右边:符号相同项a的平方减去符号相反项b的平方.
新知讲解
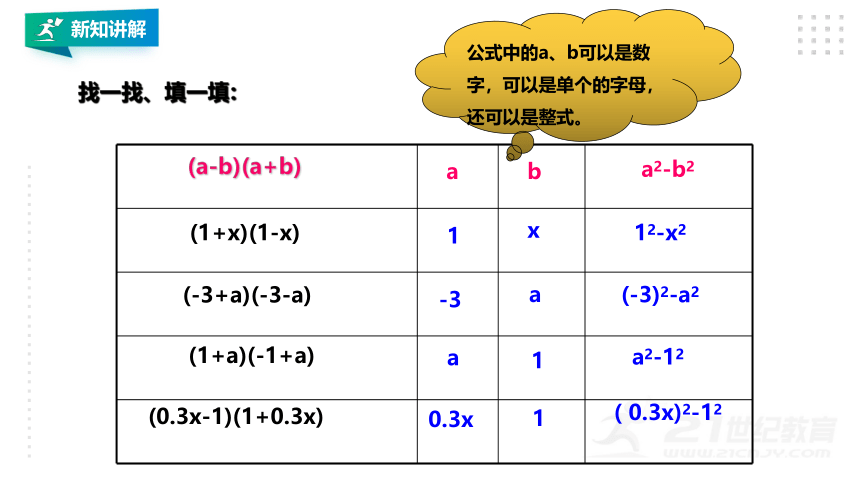
找一找、填一填:
a
b
a2-b2
1
x
12-x2
-3
a
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
(1+a)(-1+a)
(0.3x-1)(1+0.3x)
(-3+a)(-3-a)
(1+x)(1-x)
公式中的a、b可以是数字,可以是单个的字母,还可以是整式。
新知讲解
(1) (a+2b)( a 2b);
(2) (a 2b)(2b a) ;
(3) (2a+b)(b+2a);
(4) (a 3b)(a+3b) ;
(5) ( 2x+3y)(3y 2x).
(不能)
(不存在相同的项)
(不能)
(不能)
(能)
(a2 9b2)=
a2 + 9b2 ;
(不能)
判断下列式子能否用平方差公式计算:
(不存在符号相反的项)
(不存在符号相反的项)
(不存在相同的项)
注意:两个乘式中完全相同的项是a,只有符号相反的项的绝对值是b。
新知讲解
例1 运用平方差公式计算:
(1)(3x+5y)(3x-5y).
(2)
解: (1)(3x+5y)(3x-5y)
=(3x)2-(5y)2
=9x2-25y2
(2)
能否利用平方差公式进行计算,我们需要找到公式中的相同项a,相反项b,所得结果应为相同项的a的平方减去相反项b的平方.
例题讲解
运用平方差公式计算:
1、(m+n)(-n+m) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
5、 51 × 49 =
m2-n2
位置变化
y2-x2
符号变化
4a2-b2
系数变化
x4-y4
指数变化
2499
无中生有
巩固练习
例2 用平方差公式计算:
(1) 103×97 (2) 59.8×60.2
解:(1) 103×97
=(100+3)(100-3)
=1002-32
=10000-9
=9991
(2) 59.8×60.2
=(60-0.2)(60+0.2)
=602-0.22
=3600-0.04
=3599.96
通过合理变形,利用平方差公式,可以简化运算.
例题讲解
应用平方差公式计算时,应注意以下几点:
(1)左边是两个二项式相乘,并且这两个二项式中一项完全相同,
另一项互为相反数;
(2)右边是相同项的平方减去相反项的平方;
(3)公式中的a和b可以是具体的数,也可以是单项式或多项式.
新知讲解
课堂练习
2.若(2x+3y)(mx-ny)=9y2-4x2,则( )
A.m=2,n=3 B.m=-2,n=-3
C.m=2,n=-3 D.m=-2,n=3
B
1.下列运算正确的是( )
A.(a-2b)(a-2b)=a2-4b2
B.(-a+2b)(a-2b)=-a2+4b2
C.(a+2b)(-a+2b)=a2-4b2
D.(-a-2b)(-a+2b)=a2-4b2
D
4.用平方差公式计算2 018×2 016,正确的是( )
A.(2 017+1)×(2 017-1)
B.(2 017+1)×(2 018-2)
C.(2 016+2)×(2 017-1)
D.(2 015+3)×(2 015+1)
3.若x,y满足|x+y+5|+(x-y-9)2=0,则x2-y2的值为( )
A.14 B.-14
C.45 D.-45
A
D
课堂练习
5.运用平方差公式计算:
(1)(a+3b)(a-3b);
(2)(2a-5)(-2a-5);
(3)(3a+b)(9a2+b2)(3a-b).
解:(1)原式=a2-9b2.
(2)原式=a2-9b2.
(3)原式=(3a+b)(3a-b)(9a2+b2)
=(9a2-b2)(9a2+b2)
=81a4-b4.
课堂练习
6.(1)化简:a(1-2a)+2(a+1)(a-1).
解:原式=a-2a2+2(a2-1)=a-2a2+2a2-2=a-2.
(2)先化简,再求值:(x+1)(x-1)+x2(1-x)+x3,
其中x=2.
解:原式=x2-1+x2-x3+x3
=2x2-1.
将x=2代入上式,得原式=2×22-1=7.
课堂练习
7.小明将一个底为正方形,高为m的无盖盒子展开,如图①所示.
(1)请你计算无盖盒子的表面展开图的面积S1;
解:S1=a2-4m2.
(2)将图①剪拼成一个长方形,如图②所示,这个长方形的长和宽分别是多少?长方形的面积S2是多少?
解:长方形的长和宽分别为(a+2m),(a-2m),
长方形的面积S2=(a+2m)(a-2m).
(3)比较(1),(2)的结果,你得出什么结论?
解:(a+2m)(a-2m)=a2-4m2,验证了平方差公式.
课堂练方差公式
代数推导:
几何推导:
(a+b)(a-b)=a2-b2.
两数和与这两数差的积等于这两数的平方差.
课堂总结
https://www.21cnjy.com/help/help_extract.php
3.4乘法公式(1)
—平方差公式
浙教版 七年级下册
根据所学知识,计算下列多项式的积,你能发现什么规律? (1)(x+5)(x-5) = ;
(2)(3x+y)(3x-y)= ;
(3)(3m+2n)(3m–2n)= .
9 –
9 –
相乘的两个多项式的各项与它们的积中的各项有什么关系?
新知导入
你能证明(a+b)(a-b)=a2-b2吗?
方法1:利用多项式的乘法法则验证:
(a+b)(a-b)
=a2-ab+ab-b2
= a2-b2
新知讲解
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)=a2-b2
a-b
a-b
(a+b)(a-b)
方法2:利用图形的面积证明.
新知讲解
(a+b)(a-b)=a2-b2.
两数和与这两数差的积等于这两数的平方差.
平方差公式
代数推导:
文字描述:两个数的和与这两个数差的积,等于这两个数的平方差.
结构特点:
左边:a符号相同,b符号相反.
右边:符号相同项a的平方减去符号相反项b的平方.
新知讲解
找一找、填一填:
a
b
a2-b2
1
x
12-x2
-3
a
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
(1+a)(-1+a)
(0.3x-1)(1+0.3x)
(-3+a)(-3-a)
(1+x)(1-x)
公式中的a、b可以是数字,可以是单个的字母,还可以是整式。
新知讲解
(1) (a+2b)( a 2b);
(2) (a 2b)(2b a) ;
(3) (2a+b)(b+2a);
(4) (a 3b)(a+3b) ;
(5) ( 2x+3y)(3y 2x).
(不能)
(不存在相同的项)
(不能)
(不能)
(能)
(a2 9b2)=
a2 + 9b2 ;
(不能)
判断下列式子能否用平方差公式计算:
(不存在符号相反的项)
(不存在符号相反的项)
(不存在相同的项)
注意:两个乘式中完全相同的项是a,只有符号相反的项的绝对值是b。
新知讲解
例1 运用平方差公式计算:
(1)(3x+5y)(3x-5y).
(2)
解: (1)(3x+5y)(3x-5y)
=(3x)2-(5y)2
=9x2-25y2
(2)
能否利用平方差公式进行计算,我们需要找到公式中的相同项a,相反项b,所得结果应为相同项的a的平方减去相反项b的平方.
例题讲解
运用平方差公式计算:
1、(m+n)(-n+m) =
2、(-x-y) (x-y) =
3、(2a+b)(2a-b) =
4、(x2+y2)(x2-y2)=
5、 51 × 49 =
m2-n2
位置变化
y2-x2
符号变化
4a2-b2
系数变化
x4-y4
指数变化
2499
无中生有
巩固练习
例2 用平方差公式计算:
(1) 103×97 (2) 59.8×60.2
解:(1) 103×97
=(100+3)(100-3)
=1002-32
=10000-9
=9991
(2) 59.8×60.2
=(60-0.2)(60+0.2)
=602-0.22
=3600-0.04
=3599.96
通过合理变形,利用平方差公式,可以简化运算.
例题讲解
应用平方差公式计算时,应注意以下几点:
(1)左边是两个二项式相乘,并且这两个二项式中一项完全相同,
另一项互为相反数;
(2)右边是相同项的平方减去相反项的平方;
(3)公式中的a和b可以是具体的数,也可以是单项式或多项式.
新知讲解
课堂练习
2.若(2x+3y)(mx-ny)=9y2-4x2,则( )
A.m=2,n=3 B.m=-2,n=-3
C.m=2,n=-3 D.m=-2,n=3
B
1.下列运算正确的是( )
A.(a-2b)(a-2b)=a2-4b2
B.(-a+2b)(a-2b)=-a2+4b2
C.(a+2b)(-a+2b)=a2-4b2
D.(-a-2b)(-a+2b)=a2-4b2
D
4.用平方差公式计算2 018×2 016,正确的是( )
A.(2 017+1)×(2 017-1)
B.(2 017+1)×(2 018-2)
C.(2 016+2)×(2 017-1)
D.(2 015+3)×(2 015+1)
3.若x,y满足|x+y+5|+(x-y-9)2=0,则x2-y2的值为( )
A.14 B.-14
C.45 D.-45
A
D
课堂练习
5.运用平方差公式计算:
(1)(a+3b)(a-3b);
(2)(2a-5)(-2a-5);
(3)(3a+b)(9a2+b2)(3a-b).
解:(1)原式=a2-9b2.
(2)原式=a2-9b2.
(3)原式=(3a+b)(3a-b)(9a2+b2)
=(9a2-b2)(9a2+b2)
=81a4-b4.
课堂练习
6.(1)化简:a(1-2a)+2(a+1)(a-1).
解:原式=a-2a2+2(a2-1)=a-2a2+2a2-2=a-2.
(2)先化简,再求值:(x+1)(x-1)+x2(1-x)+x3,
其中x=2.
解:原式=x2-1+x2-x3+x3
=2x2-1.
将x=2代入上式,得原式=2×22-1=7.
课堂练习
7.小明将一个底为正方形,高为m的无盖盒子展开,如图①所示.
(1)请你计算无盖盒子的表面展开图的面积S1;
解:S1=a2-4m2.
(2)将图①剪拼成一个长方形,如图②所示,这个长方形的长和宽分别是多少?长方形的面积S2是多少?
解:长方形的长和宽分别为(a+2m),(a-2m),
长方形的面积S2=(a+2m)(a-2m).
(3)比较(1),(2)的结果,你得出什么结论?
解:(a+2m)(a-2m)=a2-4m2,验证了平方差公式.
课堂练方差公式
代数推导:
几何推导:
(a+b)(a-b)=a2-b2.
两数和与这两数差的积等于这两数的平方差.
课堂总结
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
