3.4乘法公式(1) 课件(共19张PPT)
文档属性
| 名称 | 3.4乘法公式(1) 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-27 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
3.4乘法公式(1)
浙教版 七年级下
情景引入
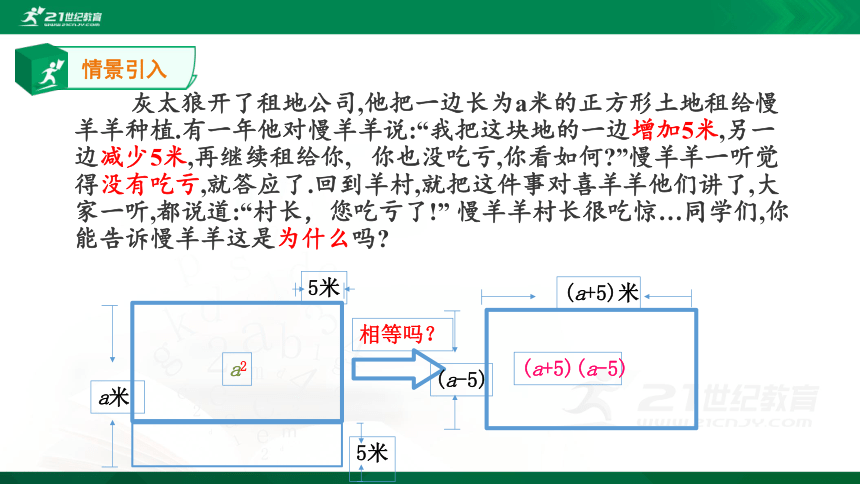
灰太狼开了租地公司,他把一边长为a米的正方形土地租给慢羊羊种植.有一年他对慢羊羊说:“我把这块地的一边增加5米,另一边减少5米,再继续租给你, 你也没吃亏,你看如何 ”慢羊羊一听觉得没有吃亏,就答应了.回到羊村,就把这件事对喜羊羊他们讲了,大家一听,都说道:“村长,您吃亏了!” 慢羊羊村长很吃惊…同学们,你能告诉慢羊羊这是为什么吗
5米
5米
a米
(a-5)
(a+5)米
相等吗?
a2
(a+5)(a-5)
新知讲解
计算下列多项式的积:
(1) (x+1)(x-1) =
(2) (m+2)(m-2) =
(3)(2x+1)(2x-1) =
=x2 - 12
=m2 - 22
=(2x)2 - 12
x2-1
m2-4
4x2-1
规律探索
从上面的计算中,你有什么发现?
新知讲解
(a+b)(a-b) = a2-b2
(a+b)(a-b)
= a2-ab+ab-b2
-ab
+ab
= a2-b2
a2
b2
你还能用其它方法证明此结论的正确性吗?
你能用代数法验证这个规律吗?
规律验证1
新知讲解
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
a-b
a-b
规律验证2
新知讲解
b
b
a
a
a-b
a-b
a
b
a-b
a
b
规律验证3
2、3利用图形面积验证等式的成立,像这样用几何图形解决代数问题的方法,体现了 的思想方法。
数形结合
新知讲解
平方差公式:
(a+b)(a- b) =
a2- b2.
即两数和与这两数差的积等于这两个数的平方差.
注:这里的两数可以是数字、字母、单项式也可以是两个多项式等.
左边:是两个二项式相乘,并且有一项完全相同;另一项互为相反数。
右边:是乘式中两项的平方差,即:
(相同项)2-(相反项)2
小试牛刀
1.选择:下列各式中,能用平方差公式的是( ) A. (x-3)(-x+3) B.(x+2y)(2x-y)
C. (y-1)(-y-1) D.(y+1)(-y-1)
2.下列多项式乘法中,能用平方差公的是
(1) (x+1)(1+x) (2) (a+b)(b-a)
(3) (-a+b)(a-b) (4) (x2-y)(x+y2)
(5) (-a-b)(a-b) (6) (c2-d2)(d2+c2)
c
(2)
(5)
(6)
小试牛刀
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
找一找,填一填
例题讲解
例1 运用平方差公式计算:
解:
例题讲解
例2 用平方差公式计算:
解:
拓展提高
1、在括号内填入怎样的代数式,才能直接运用平方差公式进行计算?
思考:平方差公式中的字母 可表示什么?
代数式.
拓展提高
2、计算:
解:
原式= 20152 - (2015-1)(2015+1)
= 20152
- (20152-12 )
= 20152
-20152+12
=1.
原式=(50+1)(50-1)
=502-12
=2500-1
=2499;
(1)51×49;
(2) 20152 - 2014×2016.
拓展提高
3、利用平方差公式计算:
(2+1)(22+1)(24+1)(28+1)+1
=(2-1)(2+1)(22+1)(24+1)(28+1)+1
=(22-1)(22+1)(24+1)(28+1)+1
=(24-1)(24+1)(28+1)+1
=(28-1)(28+1)+1
=216-1+1
=216
拓展提高
4、计算:
拓展提高
5、利用平方差公式计算:
(1) (a-2)(a+2)(a2 + 4);
解:原式=(a2-4)(a2+4)
=a4-16;
(2) (x-y)(x+y)(x2+y2)(x4+y4).
原式=(x2-y2)(x2+y2)(x4+y4)
=(x4-y4)(x4+y4)
=x8-y8.
课堂小结
这节课你学到了什么?
一个公式 (a+b)(a-b)=a2-b2
(1)简化某些多项式的乘法运算
(2)提供有理数乘法的速算方法
两种作用
三个关注
(1)要符合公式特征才能运用平方差公式
(2)公式中的a、b可以代表数字、字母或者式子(3)注意实质,善用变形创造条件用平方差公式
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
3.4乘法公式(1)
浙教版 七年级下
情景引入
灰太狼开了租地公司,他把一边长为a米的正方形土地租给慢羊羊种植.有一年他对慢羊羊说:“我把这块地的一边增加5米,另一边减少5米,再继续租给你, 你也没吃亏,你看如何 ”慢羊羊一听觉得没有吃亏,就答应了.回到羊村,就把这件事对喜羊羊他们讲了,大家一听,都说道:“村长,您吃亏了!” 慢羊羊村长很吃惊…同学们,你能告诉慢羊羊这是为什么吗
5米
5米
a米
(a-5)
(a+5)米
相等吗?
a2
(a+5)(a-5)
新知讲解
计算下列多项式的积:
(1) (x+1)(x-1) =
(2) (m+2)(m-2) =
(3)(2x+1)(2x-1) =
=x2 - 12
=m2 - 22
=(2x)2 - 12
x2-1
m2-4
4x2-1
规律探索
从上面的计算中,你有什么发现?
新知讲解
(a+b)(a-b) = a2-b2
(a+b)(a-b)
= a2-ab+ab-b2
-ab
+ab
= a2-b2
a2
b2
你还能用其它方法证明此结论的正确性吗?
你能用代数法验证这个规律吗?
规律验证1
新知讲解
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
a-b
a-b
规律验证2
新知讲解
b
b
a
a
a-b
a-b
a
b
a-b
a
b
规律验证3
2、3利用图形面积验证等式的成立,像这样用几何图形解决代数问题的方法,体现了 的思想方法。
数形结合
新知讲解
平方差公式:
(a+b)(a- b) =
a2- b2.
即两数和与这两数差的积等于这两个数的平方差.
注:这里的两数可以是数字、字母、单项式也可以是两个多项式等.
左边:是两个二项式相乘,并且有一项完全相同;另一项互为相反数。
右边:是乘式中两项的平方差,即:
(相同项)2-(相反项)2
小试牛刀
1.选择:下列各式中,能用平方差公式的是( ) A. (x-3)(-x+3) B.(x+2y)(2x-y)
C. (y-1)(-y-1) D.(y+1)(-y-1)
2.下列多项式乘法中,能用平方差公的是
(1) (x+1)(1+x) (2) (a+b)(b-a)
(3) (-a+b)(a-b) (4) (x2-y)(x+y2)
(5) (-a-b)(a-b) (6) (c2-d2)(d2+c2)
c
(2)
(5)
(6)
小试牛刀
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
找一找,填一填
例题讲解
例1 运用平方差公式计算:
解:
例题讲解
例2 用平方差公式计算:
解:
拓展提高
1、在括号内填入怎样的代数式,才能直接运用平方差公式进行计算?
思考:平方差公式中的字母 可表示什么?
代数式.
拓展提高
2、计算:
解:
原式= 20152 - (2015-1)(2015+1)
= 20152
- (20152-12 )
= 20152
-20152+12
=1.
原式=(50+1)(50-1)
=502-12
=2500-1
=2499;
(1)51×49;
(2) 20152 - 2014×2016.
拓展提高
3、利用平方差公式计算:
(2+1)(22+1)(24+1)(28+1)+1
=(2-1)(2+1)(22+1)(24+1)(28+1)+1
=(22-1)(22+1)(24+1)(28+1)+1
=(24-1)(24+1)(28+1)+1
=(28-1)(28+1)+1
=216-1+1
=216
拓展提高
4、计算:
拓展提高
5、利用平方差公式计算:
(1) (a-2)(a+2)(a2 + 4);
解:原式=(a2-4)(a2+4)
=a4-16;
(2) (x-y)(x+y)(x2+y2)(x4+y4).
原式=(x2-y2)(x2+y2)(x4+y4)
=(x4-y4)(x4+y4)
=x8-y8.
课堂小结
这节课你学到了什么?
一个公式 (a+b)(a-b)=a2-b2
(1)简化某些多项式的乘法运算
(2)提供有理数乘法的速算方法
两种作用
三个关注
(1)要符合公式特征才能运用平方差公式
(2)公式中的a、b可以代表数字、字母或者式子(3)注意实质,善用变形创造条件用平方差公式
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
