浙江版数学7年级下册第一章平行线三线八角、平行线及其判定课后强化试题 (word版 含答案)
文档属性
| 名称 | 浙江版数学7年级下册第一章平行线三线八角、平行线及其判定课后强化试题 (word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 249.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-03 00:00:00 | ||
图片预览




文档简介
三线八角、平行线及其判定课后强化练习
一、单选题
1.下列说法中正确的有( )
①一条直线的平行线只有一条.
②过一点与已知直线平行的直线只有一条.
③因为a∥b,c∥d,所以a∥d.
④经过直线外一点有且只有一条直线与已知直线平行.
A.1个 B.2个 C.3个 D.4个
2.如果两个角的一边在同一直线上,另一边互相平行,则这两个角( )
A.相等 B.互补 C.互余 D.相等或互补
3.如图,能够判定DE∥BC的条件是 ( )
A.∠DCE+∠DEC=180° B.∠EDC=∠DCB
C.∠BGF=∠DCB D.CD⊥AB,GF⊥AB
4.一辆汽车在广阔的草原上行驶,两次拐弯后,行驶的方向与原来的方向相同,那么这两次拐弯的角度可能是 ( ) .
A.第一次向右拐40°,第二次向右拐140°.
B.第一次向右拐40°,第二次向左拐40°.
C.第一次向左拐40°,第二次向右拐140°.
D.第一次向右拐140°,第二次向左拐40°.
5.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B. 若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D. 若∠3+∠5=180°,则a∥c
6.学行线后,小敏想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图,(1)—(4)):
从图中可知,小敏画平行线的依据有( )
①两直线平行,同位角相等.②两直线平行,内错角相等.③同位角相等,两直线平行.
④内错角相等,两直线平行.
A.①② B. ②③ C. ③④ D. ④①
7.下列说法中正确的个数为( )
①过一点有且只有一条直线与已知直线垂直;
②两条直线被第三条直线所截,同位角相等;
③经过两点有一条直线,并且只有一条直线;
④在同一平面内,不重合的两条直线不是平行就是相交.
A.1个 B.2个 C.3个 D.4个
8.下列说法正确的是( )
A.同一平面内不相交的两线段必平行
B.同一平面内不相交的两射线必平行
C.同一平面内不相交的一条线段与一条直线必平行
D.同一平面内不相交的两条直线必平行
9.如图,下列6种说法:①∠1与∠4是内错角;②∠1与∠2是同位角;③∠2与∠4是内错角;④∠4与∠5是同旁内角;⑤∠2与∠4是同位角;⑥∠2与∠5是内错角.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
10.如图所示,与∠α构成同位角的角的个数为( )
A.1 B.2 C.3 D.4
11.一副直角三角尺叠放如图1所示,现将含 角的三角尺ADE固定不动,将含 角的三角尺ABC绕顶点 顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当 时, ,则 )其他所有可能符合条件的度数为( )
A. 和
B. 和
C. 和
D.以上都有可能
12.下列说法正确的是( )
A.如果两条直线被第三条直线所截,那么内错角必相等
B.如果两条直线被第三条直线所截,那么同位角的角平分线必平行
C.如果同旁内角互补,那么它们的角平分线必互相垂直
D.如果两角的两边分别平行,那么这两个角必相等
13.如下图,在下列条件中,能判定AB//CD的是( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠4 D.∠3=∠4
14.下列说法:①有理数的绝对值一定是正数;②两点之间的所有连线中,线段最短;③相等的角是对顶角;④过一点有且仅有一条直线与已知直线垂直;⑤不相交的两条直线叫做平行线,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
15.如图,直线DE分别交射线BA,BG于点D,F,则下列条件中能判定 的个数是( )
① ;② ;③ ;④ .
A.1 B.2 C.3 D.4
16.如图所示,把AB,CD,EF三根木条钉在一起,使之可以在连结点M,N处自由旋转,若∠1=50°,∠2=60°,则如何旋转木条AB才能使它与木条CD平行.
小明说:把木条AB绕点M逆时针旋转10°
小刚说:把木条AB绕点M顺时针旋转170°.
以下说法中正确的是( )
A.小明的操作正确,小刚的操作错误
B.小明和小刚的操作都正确
C.小明的操作错误,小刚的操作正确
D.小明和小刚的操作都错误
17.如图,将三个相同的三角板不重叠不留空隙地拼在一起,观察图形,在线BA,AC,CE,EA,ED中,相互平行的线段有( )
A.4组 B.3组 C.2组 D.1组
18.如图,下列能判定的条件有( )个.
(1);(2);(3);(4).
A.1 B.2 C.3 D.4
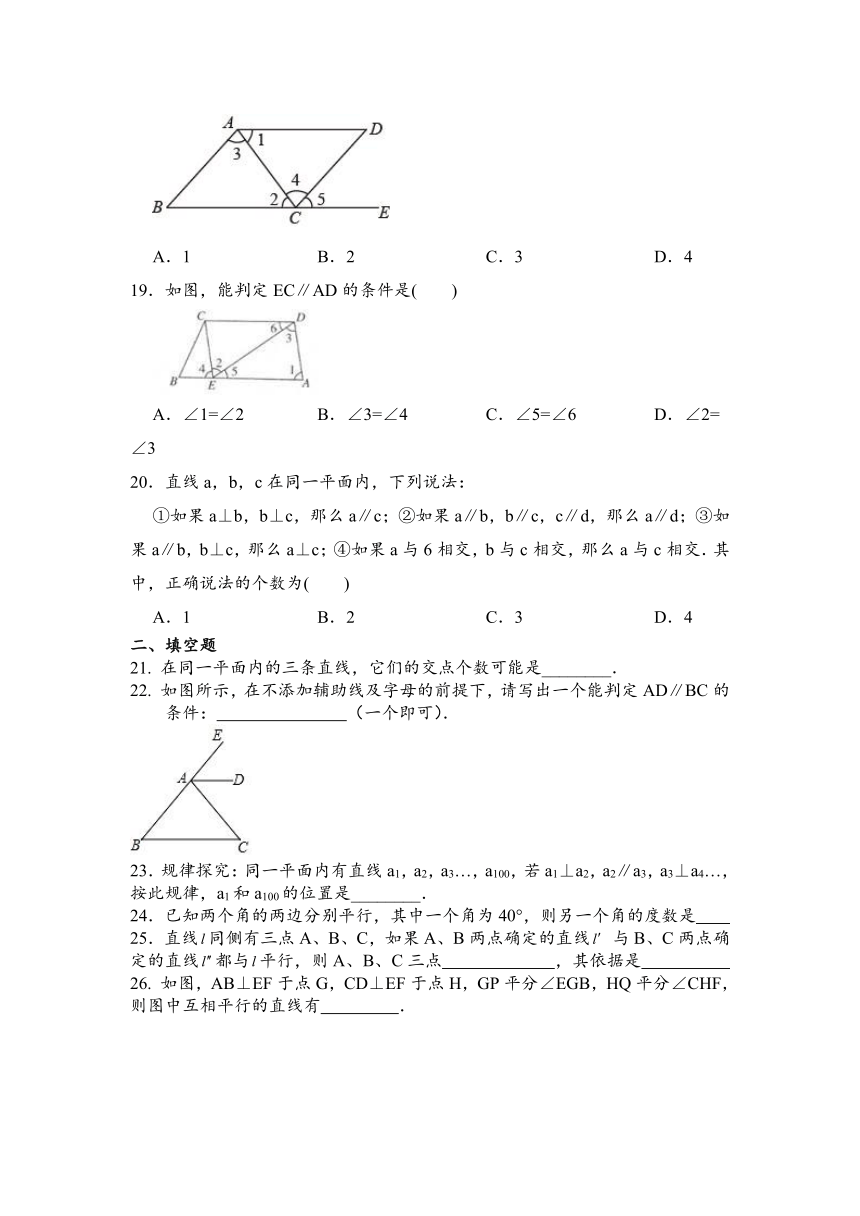
19.如图,能判定EC∥AD的条件是( )
A.∠1=∠2 B.∠3=∠4 C.∠5=∠6 D.∠2=∠3
20.直线a,b,c在同一平面内,下列说法:
①如果a⊥b,b⊥c,那么a∥c;②如果a∥b,b∥c,c∥d,那么a∥d;③如果a∥b,b⊥c,那么a⊥c;④如果a与6相交,b与c相交,那么a与c相交.其中,正确说法的个数为( )
A.1 B.2 C.3 D.4
二、填空题
21. 在同一平面内的三条直线,它们的交点个数可能是________.
22. 如图所示,在不添加辅助线及字母的前提下,请写出一个能判定AD∥BC的条件: (一个即可).
23.规律探究:同一平面内有直线a1,a2,a3…,a100,若a1⊥a2,a2∥a3,a3⊥a4…,按此规律,a1和a100的位置是________.
24.已知两个角的两边分别平行,其中一个角为40°,则另一个角的度数是
25.直线同侧有三点A、B、C,如果A、B两点确定的直线 与B、C两点确定的直线都与平行,则A、B、C三点 ,其依据是
26. 如图,AB⊥EF于点G,CD⊥EF于点H,GP平分∠EGB,HQ平分∠CHF,则图中互相平行的直线有 .
27.已知:如图,∠1=∠2,求证:AB∥CD
∵ ∠1=∠2,(已知)
又∠3=∠2,
∴∠1= .
∴ AB∥CD.( , )
三、作图题
28.如图所示,在∠AOB内有一点P.
①过P画L1∥OA;
②过P画L2∥OB;
③用量角器量一量L1与L2相交的角与∠O的大小有怎样关系?
四、解答题
29.如图,∠1=60°,∠2=60°,∠3=100°,要使AB∥EF,∠4应为多少度 说明理由.
30.如图,把一张长芳形纸条ABCD沿AF折叠,已知∠ADB=20°,那么∠BAF为多少度时,才能使AB′∥BD
31. 如图,∠ABC=∠ADC,BF、DE分别是∠ABC、∠ADC的角平分线,∠1=∠2,求证:DC∥AB.
32.如图,BCD是一条直线,∠1=∠B,∠2=∠A,指出∠1的同位角,∠2的内错角,并求出∠A+∠B+∠ACB的度数.
五、综合题
33.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线 , 被直线 所截,在这个基本图形中,形成了 对同旁内角.
(2)如图2,平面内三条直线 , , 两两相交,交点分别为A、B、C,图中一共有 对同旁内角.
(3)平面内四条直线两两相交,最多可以形成 对同旁内角.
(4)平面内n条直线两两相交,最多可以形成 对同旁内角.
34.将一副三角板中的两个直角顶点C叠放在一起(如图),其中∠A=30°,∠B=60°,∠D=∠E=45°.
(1)若∠BCD= 150° ,求∠ACE的度数;
(2)若按住三角板ABC不动,绕顶点C转动三角板DCE,试探究∠BCD等于多少度时,CD∥AB,并简要说明理由.
35.将一副直角三角尺按如图所示的方式叠放在一起(其中∠A=60°,∠D=30°,∠E=∠B=45°,直角顶点C保持重合).
(1)①若∠DCE=45°,则∠ACB的度数为 .
②若∠ACB=140°,则∠DCE的度数为 .
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)将三角尺BCE绕着点C顺时针转动,当∠ACE<180°,且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(并写明此时哪两条边平行,但不必说明理由);若不存在,请说明理由.
36.
(1)如图,已知,,求证:.
证明:∵,
∴∠ ▲ =∠ ▲ (两直线平行, ▲ )
又∵,
∴∠ ▲ =∠ ▲ ,
∴ ▲ ▲ .( ▲ ,两直线平行)
(2)如图,已知,,求证:.
答案解析部分
1. 【答案】A
2. 【答案】D
3. 【答案】B
4. 【答案】B
5. 【答案】C.
6. 【答案】C
7.【答案】B
8.【答案】D
9.【答案】C
10.【答案】C
11.【答案】B
12.【答案】C
13.【答案】C
14.【答案】A
15.【答案】C
16.【答案】B
17.【答案】C
18.【答案】C
19.【答案】D
20.【答案】C
21. 【答案】0或1或2或3个;
22. 【答案】∠B=∠EAD或∠C=∠DAC或∠B+∠BAD=180°.
23. 【答案】a1∥a100;
24.【答案】 40°或140°
25.【答案】共线,平行公理;
26【答案】AB∥CD,GP∥HQ;
27.【答案】对顶角相等;∠3;等量代换;同位角相等;两直线平行
28.【答案】①②如图所示
③L1与L2夹角有两个,∠1,∠2,∠1=∠O,∠2+∠O=180°,所以L1和L2夹角与∠O相等或互补.
29. 【答案】
解:∠4=100°.理由如下:
∵ ∠1=60°,∠2=60°,
∴ ∠1=∠2,∴ AB∥CD
又∵∠3=∠4=100°,
∴ CD∥EF,∴ AB∥EF.
30. 【答案】
解:要使AB′∥BD,只要∠B′AD=∠ADB=20°,
∠B′AB=∠BAD+∠B′AD=90°+20°=110°.
∴∠BAF=∠B′AB=×110°=55°.
31.【答案】
证明:∵BF、DE分别是∠ABC、∠ADC的角平分线
∴∠2=∠ABC,∠3=∠ADC,
∵∠ABC=∠ADC,
∴∠2=∠3,
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥DC.
32.【答案】∠1的同位角是∠B,∠2的内错角∠A,180°
33.【答案】(1)2;(2)6;(3)24;(4)
34.【答案】(1)解:∵∠BCA=∠ECD= 90°,∠BCD= 150°,
∠DCA=∠BCD-∠BCA=150°-90°=60°,
∴∠ACE=∠ECD-∠DCA=90°-60°= 30°.
(2)解:当∠BCD= 120°或60°时,CD∥AB.
理由:如图1,
∵∠B=60°,∠BCD=120°,
∴∠B+∠BCD= 180°,
∴CD∥AB;
如图2
∵∠B=60°,∠BCD=60°,
∴∠B=∠BCD,
∴CD∥AB;
35.【答案】(1)135°;40°
(2)∠ACB+∠DCE=180°.理由如下:
∵∠ACB=∠ACD+∠DCB=90°+∠DCB,
∴∠ACB+∠DCE=90°+∠DCB+∠DCE=90°+∠ECB=90°+90°=180°.
(3)(3)存在.当∠ACE=30°时,AD∥BC;当∠ACE=45°时,AC∥BE;当∠ACE=120°时,AD∥CE;当∠ACE=135°时,CD∥BE;当∠ACE=165°时,AD∥BE.
36.【答案】(1)证明:∵,
∴(两直线平行,内错角相等),
又∵,
∴,
∴.(内错角相等,两直线平行),
故答案为:2,3,内错角相等;1,2;AC,DE,内错角相等;
(2)证明:∵,
∴,
∵,
∴,
∴.
一、单选题
1.下列说法中正确的有( )
①一条直线的平行线只有一条.
②过一点与已知直线平行的直线只有一条.
③因为a∥b,c∥d,所以a∥d.
④经过直线外一点有且只有一条直线与已知直线平行.
A.1个 B.2个 C.3个 D.4个
2.如果两个角的一边在同一直线上,另一边互相平行,则这两个角( )
A.相等 B.互补 C.互余 D.相等或互补
3.如图,能够判定DE∥BC的条件是 ( )
A.∠DCE+∠DEC=180° B.∠EDC=∠DCB
C.∠BGF=∠DCB D.CD⊥AB,GF⊥AB
4.一辆汽车在广阔的草原上行驶,两次拐弯后,行驶的方向与原来的方向相同,那么这两次拐弯的角度可能是 ( ) .
A.第一次向右拐40°,第二次向右拐140°.
B.第一次向右拐40°,第二次向左拐40°.
C.第一次向左拐40°,第二次向右拐140°.
D.第一次向右拐140°,第二次向左拐40°.
5.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c B. 若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D. 若∠3+∠5=180°,则a∥c
6.学行线后,小敏想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图,(1)—(4)):
从图中可知,小敏画平行线的依据有( )
①两直线平行,同位角相等.②两直线平行,内错角相等.③同位角相等,两直线平行.
④内错角相等,两直线平行.
A.①② B. ②③ C. ③④ D. ④①
7.下列说法中正确的个数为( )
①过一点有且只有一条直线与已知直线垂直;
②两条直线被第三条直线所截,同位角相等;
③经过两点有一条直线,并且只有一条直线;
④在同一平面内,不重合的两条直线不是平行就是相交.
A.1个 B.2个 C.3个 D.4个
8.下列说法正确的是( )
A.同一平面内不相交的两线段必平行
B.同一平面内不相交的两射线必平行
C.同一平面内不相交的一条线段与一条直线必平行
D.同一平面内不相交的两条直线必平行
9.如图,下列6种说法:①∠1与∠4是内错角;②∠1与∠2是同位角;③∠2与∠4是内错角;④∠4与∠5是同旁内角;⑤∠2与∠4是同位角;⑥∠2与∠5是内错角.其中正确的有 ( )
A.1个 B.2个 C.3个 D.4个
10.如图所示,与∠α构成同位角的角的个数为( )
A.1 B.2 C.3 D.4
11.一副直角三角尺叠放如图1所示,现将含 角的三角尺ADE固定不动,将含 角的三角尺ABC绕顶点 顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当 时, ,则 )其他所有可能符合条件的度数为( )
A. 和
B. 和
C. 和
D.以上都有可能
12.下列说法正确的是( )
A.如果两条直线被第三条直线所截,那么内错角必相等
B.如果两条直线被第三条直线所截,那么同位角的角平分线必平行
C.如果同旁内角互补,那么它们的角平分线必互相垂直
D.如果两角的两边分别平行,那么这两个角必相等
13.如下图,在下列条件中,能判定AB//CD的是( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠4 D.∠3=∠4
14.下列说法:①有理数的绝对值一定是正数;②两点之间的所有连线中,线段最短;③相等的角是对顶角;④过一点有且仅有一条直线与已知直线垂直;⑤不相交的两条直线叫做平行线,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
15.如图,直线DE分别交射线BA,BG于点D,F,则下列条件中能判定 的个数是( )
① ;② ;③ ;④ .
A.1 B.2 C.3 D.4
16.如图所示,把AB,CD,EF三根木条钉在一起,使之可以在连结点M,N处自由旋转,若∠1=50°,∠2=60°,则如何旋转木条AB才能使它与木条CD平行.
小明说:把木条AB绕点M逆时针旋转10°
小刚说:把木条AB绕点M顺时针旋转170°.
以下说法中正确的是( )
A.小明的操作正确,小刚的操作错误
B.小明和小刚的操作都正确
C.小明的操作错误,小刚的操作正确
D.小明和小刚的操作都错误
17.如图,将三个相同的三角板不重叠不留空隙地拼在一起,观察图形,在线BA,AC,CE,EA,ED中,相互平行的线段有( )
A.4组 B.3组 C.2组 D.1组
18.如图,下列能判定的条件有( )个.
(1);(2);(3);(4).
A.1 B.2 C.3 D.4
19.如图,能判定EC∥AD的条件是( )
A.∠1=∠2 B.∠3=∠4 C.∠5=∠6 D.∠2=∠3
20.直线a,b,c在同一平面内,下列说法:
①如果a⊥b,b⊥c,那么a∥c;②如果a∥b,b∥c,c∥d,那么a∥d;③如果a∥b,b⊥c,那么a⊥c;④如果a与6相交,b与c相交,那么a与c相交.其中,正确说法的个数为( )
A.1 B.2 C.3 D.4
二、填空题
21. 在同一平面内的三条直线,它们的交点个数可能是________.
22. 如图所示,在不添加辅助线及字母的前提下,请写出一个能判定AD∥BC的条件: (一个即可).
23.规律探究:同一平面内有直线a1,a2,a3…,a100,若a1⊥a2,a2∥a3,a3⊥a4…,按此规律,a1和a100的位置是________.
24.已知两个角的两边分别平行,其中一个角为40°,则另一个角的度数是
25.直线同侧有三点A、B、C,如果A、B两点确定的直线 与B、C两点确定的直线都与平行,则A、B、C三点 ,其依据是
26. 如图,AB⊥EF于点G,CD⊥EF于点H,GP平分∠EGB,HQ平分∠CHF,则图中互相平行的直线有 .
27.已知:如图,∠1=∠2,求证:AB∥CD
∵ ∠1=∠2,(已知)
又∠3=∠2,
∴∠1= .
∴ AB∥CD.( , )
三、作图题
28.如图所示,在∠AOB内有一点P.
①过P画L1∥OA;
②过P画L2∥OB;
③用量角器量一量L1与L2相交的角与∠O的大小有怎样关系?
四、解答题
29.如图,∠1=60°,∠2=60°,∠3=100°,要使AB∥EF,∠4应为多少度 说明理由.
30.如图,把一张长芳形纸条ABCD沿AF折叠,已知∠ADB=20°,那么∠BAF为多少度时,才能使AB′∥BD
31. 如图,∠ABC=∠ADC,BF、DE分别是∠ABC、∠ADC的角平分线,∠1=∠2,求证:DC∥AB.
32.如图,BCD是一条直线,∠1=∠B,∠2=∠A,指出∠1的同位角,∠2的内错角,并求出∠A+∠B+∠ACB的度数.
五、综合题
33.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线 , 被直线 所截,在这个基本图形中,形成了 对同旁内角.
(2)如图2,平面内三条直线 , , 两两相交,交点分别为A、B、C,图中一共有 对同旁内角.
(3)平面内四条直线两两相交,最多可以形成 对同旁内角.
(4)平面内n条直线两两相交,最多可以形成 对同旁内角.
34.将一副三角板中的两个直角顶点C叠放在一起(如图),其中∠A=30°,∠B=60°,∠D=∠E=45°.
(1)若∠BCD= 150° ,求∠ACE的度数;
(2)若按住三角板ABC不动,绕顶点C转动三角板DCE,试探究∠BCD等于多少度时,CD∥AB,并简要说明理由.
35.将一副直角三角尺按如图所示的方式叠放在一起(其中∠A=60°,∠D=30°,∠E=∠B=45°,直角顶点C保持重合).
(1)①若∠DCE=45°,则∠ACB的度数为 .
②若∠ACB=140°,则∠DCE的度数为 .
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)将三角尺BCE绕着点C顺时针转动,当∠ACE<180°,且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(并写明此时哪两条边平行,但不必说明理由);若不存在,请说明理由.
36.
(1)如图,已知,,求证:.
证明:∵,
∴∠ ▲ =∠ ▲ (两直线平行, ▲ )
又∵,
∴∠ ▲ =∠ ▲ ,
∴ ▲ ▲ .( ▲ ,两直线平行)
(2)如图,已知,,求证:.
答案解析部分
1. 【答案】A
2. 【答案】D
3. 【答案】B
4. 【答案】B
5. 【答案】C.
6. 【答案】C
7.【答案】B
8.【答案】D
9.【答案】C
10.【答案】C
11.【答案】B
12.【答案】C
13.【答案】C
14.【答案】A
15.【答案】C
16.【答案】B
17.【答案】C
18.【答案】C
19.【答案】D
20.【答案】C
21. 【答案】0或1或2或3个;
22. 【答案】∠B=∠EAD或∠C=∠DAC或∠B+∠BAD=180°.
23. 【答案】a1∥a100;
24.【答案】 40°或140°
25.【答案】共线,平行公理;
26【答案】AB∥CD,GP∥HQ;
27.【答案】对顶角相等;∠3;等量代换;同位角相等;两直线平行
28.【答案】①②如图所示
③L1与L2夹角有两个,∠1,∠2,∠1=∠O,∠2+∠O=180°,所以L1和L2夹角与∠O相等或互补.
29. 【答案】
解:∠4=100°.理由如下:
∵ ∠1=60°,∠2=60°,
∴ ∠1=∠2,∴ AB∥CD
又∵∠3=∠4=100°,
∴ CD∥EF,∴ AB∥EF.
30. 【答案】
解:要使AB′∥BD,只要∠B′AD=∠ADB=20°,
∠B′AB=∠BAD+∠B′AD=90°+20°=110°.
∴∠BAF=∠B′AB=×110°=55°.
31.【答案】
证明:∵BF、DE分别是∠ABC、∠ADC的角平分线
∴∠2=∠ABC,∠3=∠ADC,
∵∠ABC=∠ADC,
∴∠2=∠3,
又∵∠1=∠2,
∴∠1=∠3,
∴AB∥DC.
32.【答案】∠1的同位角是∠B,∠2的内错角∠A,180°
33.【答案】(1)2;(2)6;(3)24;(4)
34.【答案】(1)解:∵∠BCA=∠ECD= 90°,∠BCD= 150°,
∠DCA=∠BCD-∠BCA=150°-90°=60°,
∴∠ACE=∠ECD-∠DCA=90°-60°= 30°.
(2)解:当∠BCD= 120°或60°时,CD∥AB.
理由:如图1,
∵∠B=60°,∠BCD=120°,
∴∠B+∠BCD= 180°,
∴CD∥AB;
如图2
∵∠B=60°,∠BCD=60°,
∴∠B=∠BCD,
∴CD∥AB;
35.【答案】(1)135°;40°
(2)∠ACB+∠DCE=180°.理由如下:
∵∠ACB=∠ACD+∠DCB=90°+∠DCB,
∴∠ACB+∠DCE=90°+∠DCB+∠DCE=90°+∠ECB=90°+90°=180°.
(3)(3)存在.当∠ACE=30°时,AD∥BC;当∠ACE=45°时,AC∥BE;当∠ACE=120°时,AD∥CE;当∠ACE=135°时,CD∥BE;当∠ACE=165°时,AD∥BE.
36.【答案】(1)证明:∵,
∴(两直线平行,内错角相等),
又∵,
∴,
∴.(内错角相等,两直线平行),
故答案为:2,3,内错角相等;1,2;AC,DE,内错角相等;
(2)证明:∵,
∴,
∵,
∴,
∴.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
