5.3 多项式的乘法
图片预览




文档简介
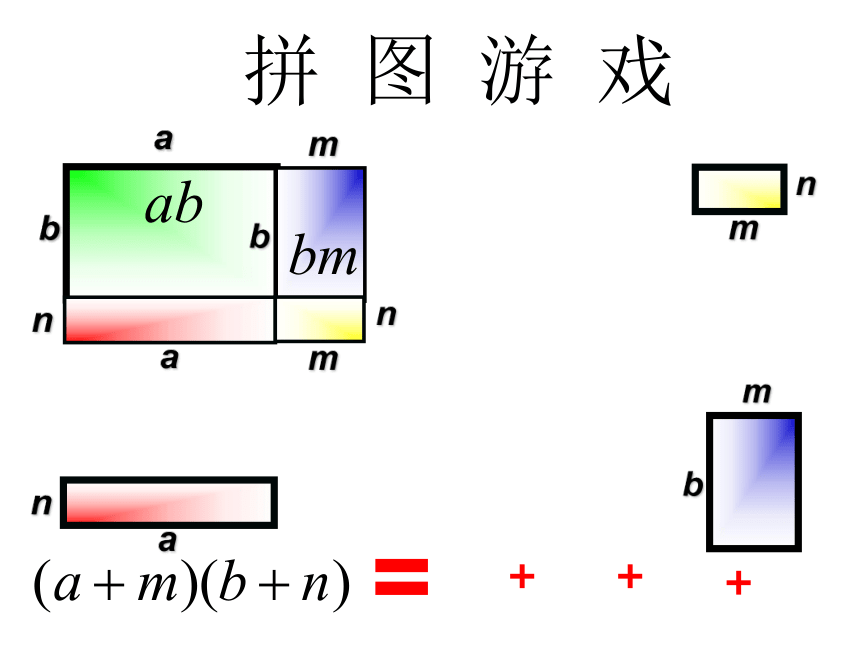
课件11张PPT。5.3 多项式的乘法拼 图 游 戏+++?=多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
即(a+m)(b+n) = a(b+n) + m (b+n)
=ab+an+mb+mn.X X X (a+b)(m+n)=am+an+bm+bn1234例题解析 【例】计算: (1)(1?x)(0.6?x); (2)(2x + y)(x?y)。所得积的符号由这
两项的符号来确定:??1?x?x? 0.6+=0.6?1.6x+x2 ; ??x? x负负得正
一正一负得负。(2) (2x + y)(x?y)=2xx2x?x2x?y?2x? y+ y+ y? x+??y?y=2x2?2xy+ xy?y2=2x2 ?xy?y2. ?最后的结果要合并同类项. (1) (2x–3)(x+4) ;计算:(2)(2a-b)2=(2a-b)(2a-b)=4a2-2ab-2ab+b2=4a2-4ab+b2自主尝试多项式乘以多项式,展开后项数有什么规律?在合并同类项之前,展开式的项数恰好
等于两个多项式的项数的积。注意:
1、注意多项式中每一项的符号;
2、运用法则’做到不重不漏’按序进行;
3、没有合并同类项之前,积的项数
等于 各个多项式项数的积;
4、结果要合并同类项,化为最简形式。
课内练习1作业题1(3) (4)1. 先化简,再求值:
(2a-3)(3a+1)-6a(a-4) 其中a=
综合与运用2.化简:(2x-1)(-3x)-(1-3x)(1+2x)3.先化简,再求值:
(x+3)(x-3)-x(x-6),其中x=2若含有与多项式的积差的运算,后两个多项式
乘积的展开式要用括号括起来。2若含有数与多项式的积相乘的运算,可先将多项式乘积展开,再用括号括起来。作业题2 3P115作业题4,5在一块长为a m,宽为b m的长方形荒地中央建造一个花园,在花园四周修建宽度是x m的小路,求花园的面积。ab填空:观察上面四个等式,你能发现什么规律?你能根据这个规律解决下面的问题吗?5 61 (-6)(-1) (-6)(-5) 6口答:拓展与探索知识回眸小结:
1.运用多项式的乘法法则时,必须做到不重不漏.
2.注意确定积中的每一项的符号,多项式中每一项都包含它前面的符号,“同号得正,异号得负”.
3.多项式与多项式想乘的展开式中,有同类项要合并同类项. 课件11张PPT。5.3 多项式的乘法拼 图 游 戏+++?=多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
即(a+m)(b+n) = a(b+n) + m (b+n)
=ab+an+mb+mn.X X X (a+b)(m+n)=am+an+bm+bn1234例题解析 【例】计算: 阅读 ? 体验 ? (1)(1?x)(0.6?x); (2)(2x + y)(x?y)。所得积的符号由这
两项的符号来确定:??1?x?x? 0.6+=0.6?1.6x+x2 ; ??x? x负负得正
一正一负得负。(2) (2x + y)(x?y)=2xx2x?x2x?y?2x? y+ y+ y? x+??y?y=2x2?2xy+ xy?y2=2x2 ?xy?y2. ?最后的结果要合并同类项. (1) (2x–3)(x+4) ;计算:(2)(2a-b)2=(2a-b)(2a-b)=4a2-2ab-2ab+b2=4a2-4ab+b2自主尝试多项式乘以多项式,展开后项数有什么规律?在合并同类项之前,展开式的项数恰好
等于两个多项式的项数的积。注意:
1、注意多项式中每一项的符号;
2、运用法则’做到不重不漏’按序进行;
3、没有合并同类项之前,积的项数
等于 各个多项式项数的积;
4、结果要合并同类项,化为最简形式。
课内练习1作业题1(3) (4)1. 先化简,再求值:
(2a-3)(3a+1)-6a(a-4) 其中a=
综合与运用2.化简:(2x-1)(-3x)-(1-3x)(1+2x)3.先化简,再求值:
(x+3)(x-3)-x(x-6),其中x=2若含有与多项式的积差的运算,后两个多项式
乘积的展开式要用括号括起来。2若含有数与多项式的积相乘的运算,可先将多项式乘积展开,再用括号括起来。作业题2 3P115作业题4,5在一块长为a m,宽为b m的长方形荒地中央建造一个花园,在花园四周修建宽度是x m的小路,求花园的面积。ab填空:观察上面四个等式,你能发现什么规律?你能根据这个规律解决下面的问题吗?5 61 (-6)(-1) (-6)(-5) 6口答:拓展与探索知识回眸小结:
1.运用多项式的乘法法则时,必须做到不重不漏.
2.注意确定积中的每一项的符号,多项式中每一项都包含它前面的符号,“同号得正,异号得负”.
3.多项式与多项式想乘的展开式中,有同类项要合并同类项.
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
即(a+m)(b+n) = a(b+n) + m (b+n)
=ab+an+mb+mn.X X X (a+b)(m+n)=am+an+bm+bn1234例题解析 【例】计算: (1)(1?x)(0.6?x); (2)(2x + y)(x?y)。所得积的符号由这
两项的符号来确定:??1?x?x? 0.6+=0.6?1.6x+x2 ; ??x? x负负得正
一正一负得负。(2) (2x + y)(x?y)=2xx2x?x2x?y?2x? y+ y+ y? x+??y?y=2x2?2xy+ xy?y2=2x2 ?xy?y2. ?最后的结果要合并同类项. (1) (2x–3)(x+4) ;计算:(2)(2a-b)2=(2a-b)(2a-b)=4a2-2ab-2ab+b2=4a2-4ab+b2自主尝试多项式乘以多项式,展开后项数有什么规律?在合并同类项之前,展开式的项数恰好
等于两个多项式的项数的积。注意:
1、注意多项式中每一项的符号;
2、运用法则’做到不重不漏’按序进行;
3、没有合并同类项之前,积的项数
等于 各个多项式项数的积;
4、结果要合并同类项,化为最简形式。
课内练习1作业题1(3) (4)1. 先化简,再求值:
(2a-3)(3a+1)-6a(a-4) 其中a=
综合与运用2.化简:(2x-1)(-3x)-(1-3x)(1+2x)3.先化简,再求值:
(x+3)(x-3)-x(x-6),其中x=2若含有与多项式的积差的运算,后两个多项式
乘积的展开式要用括号括起来。2若含有数与多项式的积相乘的运算,可先将多项式乘积展开,再用括号括起来。作业题2 3P115作业题4,5在一块长为a m,宽为b m的长方形荒地中央建造一个花园,在花园四周修建宽度是x m的小路,求花园的面积。ab填空:观察上面四个等式,你能发现什么规律?你能根据这个规律解决下面的问题吗?5 61 (-6)(-1) (-6)(-5) 6口答:拓展与探索知识回眸小结:
1.运用多项式的乘法法则时,必须做到不重不漏.
2.注意确定积中的每一项的符号,多项式中每一项都包含它前面的符号,“同号得正,异号得负”.
3.多项式与多项式想乘的展开式中,有同类项要合并同类项. 课件11张PPT。5.3 多项式的乘法拼 图 游 戏+++?=多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
即(a+m)(b+n) = a(b+n) + m (b+n)
=ab+an+mb+mn.X X X (a+b)(m+n)=am+an+bm+bn1234例题解析 【例】计算: 阅读 ? 体验 ? (1)(1?x)(0.6?x); (2)(2x + y)(x?y)。所得积的符号由这
两项的符号来确定:??1?x?x? 0.6+=0.6?1.6x+x2 ; ??x? x负负得正
一正一负得负。(2) (2x + y)(x?y)=2xx2x?x2x?y?2x? y+ y+ y? x+??y?y=2x2?2xy+ xy?y2=2x2 ?xy?y2. ?最后的结果要合并同类项. (1) (2x–3)(x+4) ;计算:(2)(2a-b)2=(2a-b)(2a-b)=4a2-2ab-2ab+b2=4a2-4ab+b2自主尝试多项式乘以多项式,展开后项数有什么规律?在合并同类项之前,展开式的项数恰好
等于两个多项式的项数的积。注意:
1、注意多项式中每一项的符号;
2、运用法则’做到不重不漏’按序进行;
3、没有合并同类项之前,积的项数
等于 各个多项式项数的积;
4、结果要合并同类项,化为最简形式。
课内练习1作业题1(3) (4)1. 先化简,再求值:
(2a-3)(3a+1)-6a(a-4) 其中a=
综合与运用2.化简:(2x-1)(-3x)-(1-3x)(1+2x)3.先化简,再求值:
(x+3)(x-3)-x(x-6),其中x=2若含有与多项式的积差的运算,后两个多项式
乘积的展开式要用括号括起来。2若含有数与多项式的积相乘的运算,可先将多项式乘积展开,再用括号括起来。作业题2 3P115作业题4,5在一块长为a m,宽为b m的长方形荒地中央建造一个花园,在花园四周修建宽度是x m的小路,求花园的面积。ab填空:观察上面四个等式,你能发现什么规律?你能根据这个规律解决下面的问题吗?5 61 (-6)(-1) (-6)(-5) 6口答:拓展与探索知识回眸小结:
1.运用多项式的乘法法则时,必须做到不重不漏.
2.注意确定积中的每一项的符号,多项式中每一项都包含它前面的符号,“同号得正,异号得负”.
3.多项式与多项式想乘的展开式中,有同类项要合并同类项.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
