4.3 用乘法公式分解因式(2) 课件(共20张PPT)
文档属性
| 名称 | 4.3 用乘法公式分解因式(2) 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-16 16:10:04 | ||
图片预览








文档简介
(共20张PPT)
4.3 用乘法公式分解因式(2)
浙教版 七年级下册
1.因式分解:
把一个多项式转化为几个整式的积的形式.
2.我们已经学过哪些因式分解的方法?
1.提公因式法
2.平方差公式逆用
a2-b2=(a+b)(a-b)
今天我们学习用公式因式分解的另一个公式:完全平方公式.
新知引入
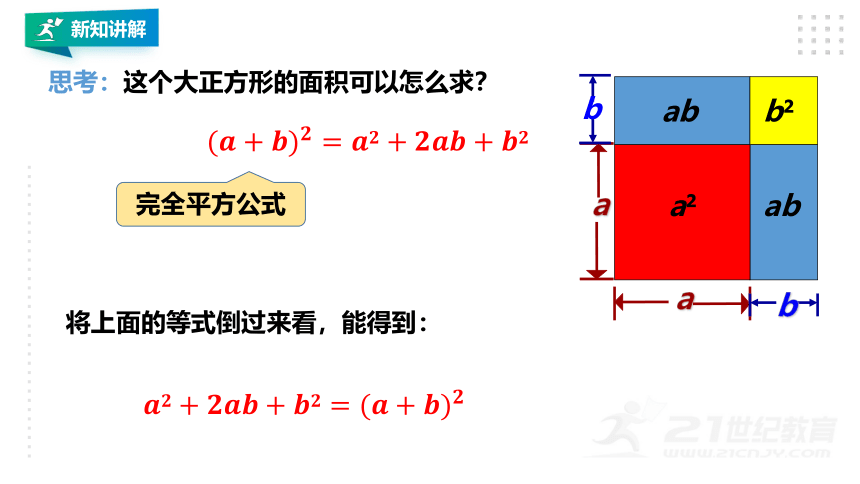
思考:这个大正方形的面积可以怎么求?
a
b
a
b
a
ab
ab
b
将上面的等式倒过来看,能得到:
完全平方公式
新知讲解
由乘法的完全平方公式:
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2,
可得:a2+2ab+b2=(a+b)2, a2-2ab+b2=(a-b)2
我们把多项式a2+2ab+b2及a2-2ab+b2叫做完全平方式.
完全平方公式
两数的平方和,加上(或者减去)这两数的积的2倍,
等于这两数和(或者差)的平方.
新知讲解
完全平方式的特点:
1. 三项式(或可以看成三项的);
2. 有两项为数或式的平方和;
3. 有一项为两数或式乘积的2倍,与符号无关.
简记口诀:“首平方,尾平方,首尾两倍在中央”.
2
a
b
+b2
±
=(a ± b)
a2
首2
+尾2
±2×首×尾
(首±尾)2
新知讲解
下列各式是不是完全平方式?
(1);
(2);
(3);
(4);
(5).
不是,它只有两项;
不是,与的符号不统一;
不是,因为不是与的积的2倍;
是;
是.
巩固练习
一般地,利用公式 a2-b2=(a+b)(a-b),或a2±2ab+b2=(a±b)2把一个多项式分解因式的方法,叫做公式法.
公式法
注意:公式中的a,b可以是数,也可以是整式.
新知讲解
整式乘法
因式分解
(a±b)2
完全平方公式与因式分解关系:
新知讲解
新知讲解
例3 把下列各式分解因式:
(1)4a2+12ab+9b2. (2) -x2+4xy-4y2. (3) 3ax2+6axy+3ay2.
解: (1) 4a2+12ab+9b2 =(2a)2+2·(2a)·(3b)+(3b)2
=(2a+3b)2.
(2) -x2+4xy-4y2 =-(x2-4xy+4y2)
=-[x2-2·x·(2y)+(2y)2]
=-(x-2y)2.
(3) 3ax2+6axy+3ay2 =3a(x2+2xy+y2)
=3a(x+y)2.
先提公因式,再套用公式,平方项为负的先提出负号.
注意分解因式必须进行到每一个多项式都不能再分解因式为止.
因式分解:
(1)-3a2x2+24a2x-48a2;
(2)(a2+4)2-16a2.
=(a2+4+4a)(a2+4-4a)
解:(1)原式=-3a2(x2-8x+16)
=-3a2(x-4)2;
(2)原式=(a2+4)2-(4a)2
=(a+2)2(a-2)2.
有公因式要先提公因式
要检查每一个多项式的因式,看能否继续分解.
巩固练习
例4 分解因式:(2x+y)2-6(2x+y)+9.
解: (2x+y)2-6(2x+y)+9
=(2x+y)2-2·(2x+y)·3+32
=[(2x+y)-3]2
=(2x+y-3)2.
分析:把(2x+y)看做一个整体,多项式就是一个关于(2x+y)的完全平方式.
注意:公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成完全平方的形式,就能用完全平方公式因式分解.
新知讲解
分解因式:
(m+n)2-6(m+n)+9.
解:原式=[(m+n)-3]2
=(m+n-3)2.
把(m+n)看成一个整体,所以(m+n)2-6(m+n)+9是一个完全平方式.
巩固练习
一
先提公因式(有公因式)
二
平方差公式(剩余两项)
三
完全平方公式(剩余三项)
四
结果必须到不能分解为止
有一些可以用整体的思想看成两项或三项
因式分解的方法与步骤;
总结归纳
课堂练习
1. 下列各式中能用完全平方公式进行因式分解的是( )
A.x2+x+1 B.x2+2x-1
C.x2-1 D.x2-6x+9
D
2. 已知x2+16x+k是完全平方式,则常数k等于( )
A.64 B.48
C.32 D.16
A
3. 若代数式x2+kx+25是一个完全平方式,则k=____ .
±10
4.因式分解:
.
课堂练习
5.对照 a ±2ab+b =(a±b) ,填空:
③.a +4ab+4b =( ) +2· ( ) ·( )+( ) =( )
②.m -6m+9=( ) - 2· ( ) ·( )+( ) =( )
①. x +4x+4= ( ) +2·( )·( )+( ) =( )
x
2
x + 2
a
a 2b
a + 2b
2b
m
m - 3
3
x
2
m
3
课堂练习
6. 分解因式:
(1)x2-12x+36; (2)-x2+4xy-4y2;
(3)4(2a+b)2-4(2a+b)+1;(4)y2+2y+1-x2
解:(1)原式 =x2-2·x·6+(6)2
=(x-6)2;
(2)原式 =-(x2-4xy+4y2)
=-(x-2y)2;
(3)原式=[2(2a+b)] - 2·2(2a+b)·1+(1)
=(4a+2b - 1)2;
(4)原式=(y+1) -x
=(y+1+x)(y+1-x).
课堂练习
7.(1)已知a-b=3,求a(a-2b)+b2的值;
(2)已知ab=2,a+b=5,求a3b+2a2b2+ab3的值.
解:(1)∵a-b=3,
∴a(a-2b)+b2=a2-2ab+b2
=(a-b)2
=32=9.
(2)∵ab=2,a+b=5,
∴a3b+2a2b2+ab3=ab(a2+2ab+b2)
=ab(a+b)2
=2×52=50.
课堂练习
课堂总结
公 式 法
分 解 因 式
(完全平方公式)
公 式
(1)要求多项式有三项.
(2)其中两项同号,且都可以写成某数或式的平方,另一项则是这两数或式的乘积的2倍,符号可正可负.
特 点
https://www.21cnjy.com/help/help_extract.php
4.3 用乘法公式分解因式(2)
浙教版 七年级下册
1.因式分解:
把一个多项式转化为几个整式的积的形式.
2.我们已经学过哪些因式分解的方法?
1.提公因式法
2.平方差公式逆用
a2-b2=(a+b)(a-b)
今天我们学习用公式因式分解的另一个公式:完全平方公式.
新知引入
思考:这个大正方形的面积可以怎么求?
a
b
a
b
a
ab
ab
b
将上面的等式倒过来看,能得到:
完全平方公式
新知讲解
由乘法的完全平方公式:
(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2,
可得:a2+2ab+b2=(a+b)2, a2-2ab+b2=(a-b)2
我们把多项式a2+2ab+b2及a2-2ab+b2叫做完全平方式.
完全平方公式
两数的平方和,加上(或者减去)这两数的积的2倍,
等于这两数和(或者差)的平方.
新知讲解
完全平方式的特点:
1. 三项式(或可以看成三项的);
2. 有两项为数或式的平方和;
3. 有一项为两数或式乘积的2倍,与符号无关.
简记口诀:“首平方,尾平方,首尾两倍在中央”.
2
a
b
+b2
±
=(a ± b)
a2
首2
+尾2
±2×首×尾
(首±尾)2
新知讲解
下列各式是不是完全平方式?
(1);
(2);
(3);
(4);
(5).
不是,它只有两项;
不是,与的符号不统一;
不是,因为不是与的积的2倍;
是;
是.
巩固练习
一般地,利用公式 a2-b2=(a+b)(a-b),或a2±2ab+b2=(a±b)2把一个多项式分解因式的方法,叫做公式法.
公式法
注意:公式中的a,b可以是数,也可以是整式.
新知讲解
整式乘法
因式分解
(a±b)2
完全平方公式与因式分解关系:
新知讲解
新知讲解
例3 把下列各式分解因式:
(1)4a2+12ab+9b2. (2) -x2+4xy-4y2. (3) 3ax2+6axy+3ay2.
解: (1) 4a2+12ab+9b2 =(2a)2+2·(2a)·(3b)+(3b)2
=(2a+3b)2.
(2) -x2+4xy-4y2 =-(x2-4xy+4y2)
=-[x2-2·x·(2y)+(2y)2]
=-(x-2y)2.
(3) 3ax2+6axy+3ay2 =3a(x2+2xy+y2)
=3a(x+y)2.
先提公因式,再套用公式,平方项为负的先提出负号.
注意分解因式必须进行到每一个多项式都不能再分解因式为止.
因式分解:
(1)-3a2x2+24a2x-48a2;
(2)(a2+4)2-16a2.
=(a2+4+4a)(a2+4-4a)
解:(1)原式=-3a2(x2-8x+16)
=-3a2(x-4)2;
(2)原式=(a2+4)2-(4a)2
=(a+2)2(a-2)2.
有公因式要先提公因式
要检查每一个多项式的因式,看能否继续分解.
巩固练习
例4 分解因式:(2x+y)2-6(2x+y)+9.
解: (2x+y)2-6(2x+y)+9
=(2x+y)2-2·(2x+y)·3+32
=[(2x+y)-3]2
=(2x+y-3)2.
分析:把(2x+y)看做一个整体,多项式就是一个关于(2x+y)的完全平方式.
注意:公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成完全平方的形式,就能用完全平方公式因式分解.
新知讲解
分解因式:
(m+n)2-6(m+n)+9.
解:原式=[(m+n)-3]2
=(m+n-3)2.
把(m+n)看成一个整体,所以(m+n)2-6(m+n)+9是一个完全平方式.
巩固练习
一
先提公因式(有公因式)
二
平方差公式(剩余两项)
三
完全平方公式(剩余三项)
四
结果必须到不能分解为止
有一些可以用整体的思想看成两项或三项
因式分解的方法与步骤;
总结归纳
课堂练习
1. 下列各式中能用完全平方公式进行因式分解的是( )
A.x2+x+1 B.x2+2x-1
C.x2-1 D.x2-6x+9
D
2. 已知x2+16x+k是完全平方式,则常数k等于( )
A.64 B.48
C.32 D.16
A
3. 若代数式x2+kx+25是一个完全平方式,则k=____ .
±10
4.因式分解:
.
课堂练习
5.对照 a ±2ab+b =(a±b) ,填空:
③.a +4ab+4b =( ) +2· ( ) ·( )+( ) =( )
②.m -6m+9=( ) - 2· ( ) ·( )+( ) =( )
①. x +4x+4= ( ) +2·( )·( )+( ) =( )
x
2
x + 2
a
a 2b
a + 2b
2b
m
m - 3
3
x
2
m
3
课堂练习
6. 分解因式:
(1)x2-12x+36; (2)-x2+4xy-4y2;
(3)4(2a+b)2-4(2a+b)+1;(4)y2+2y+1-x2
解:(1)原式 =x2-2·x·6+(6)2
=(x-6)2;
(2)原式 =-(x2-4xy+4y2)
=-(x-2y)2;
(3)原式=[2(2a+b)] - 2·2(2a+b)·1+(1)
=(4a+2b - 1)2;
(4)原式=(y+1) -x
=(y+1+x)(y+1-x).
课堂练习
7.(1)已知a-b=3,求a(a-2b)+b2的值;
(2)已知ab=2,a+b=5,求a3b+2a2b2+ab3的值.
解:(1)∵a-b=3,
∴a(a-2b)+b2=a2-2ab+b2
=(a-b)2
=32=9.
(2)∵ab=2,a+b=5,
∴a3b+2a2b2+ab3=ab(a2+2ab+b2)
=ab(a+b)2
=2×52=50.
课堂练习
课堂总结
公 式 法
分 解 因 式
(完全平方公式)
公 式
(1)要求多项式有三项.
(2)其中两项同号,且都可以写成某数或式的平方,另一项则是这两数或式的乘积的2倍,符号可正可负.
特 点
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
