1.2同位角、内错角、同旁内角

(共22张PPT)
§1.2
3
1
2
4
相交
3
1
2
4
7
5
6
8
a
b
c
你能描述你所看到的图形吗？
两条直线被第三条直线所截。
(直线a、b被直线c所截)
截线
被截线
1
4
5
8
b
a
c
2
1
4
3
6
5
8
7
b
a
c
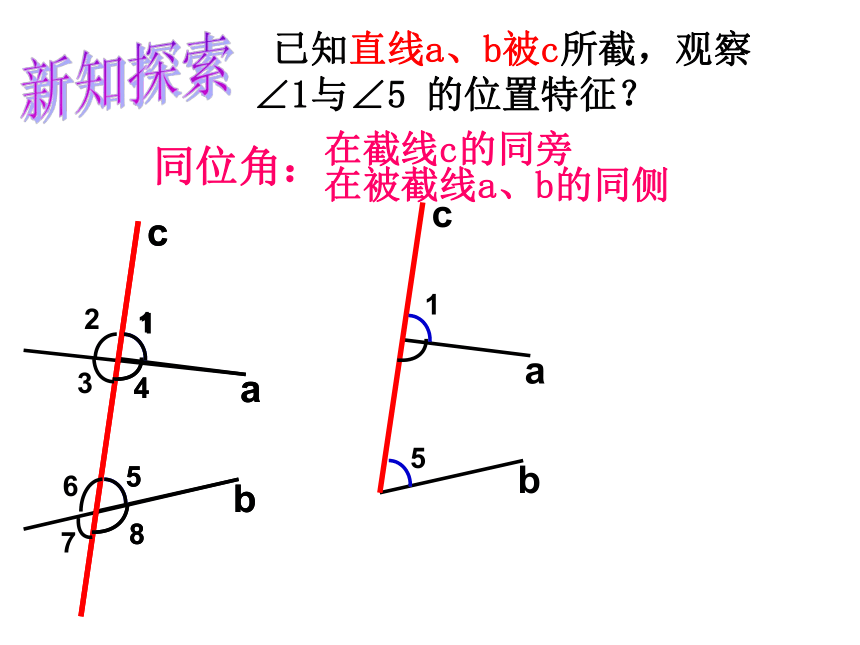
已知直线a、b被c所截，观察∠1与∠5 的位置特征？
1
5
b
a
c
同位角：
在截线c的同旁
在被截线a、b的同侧
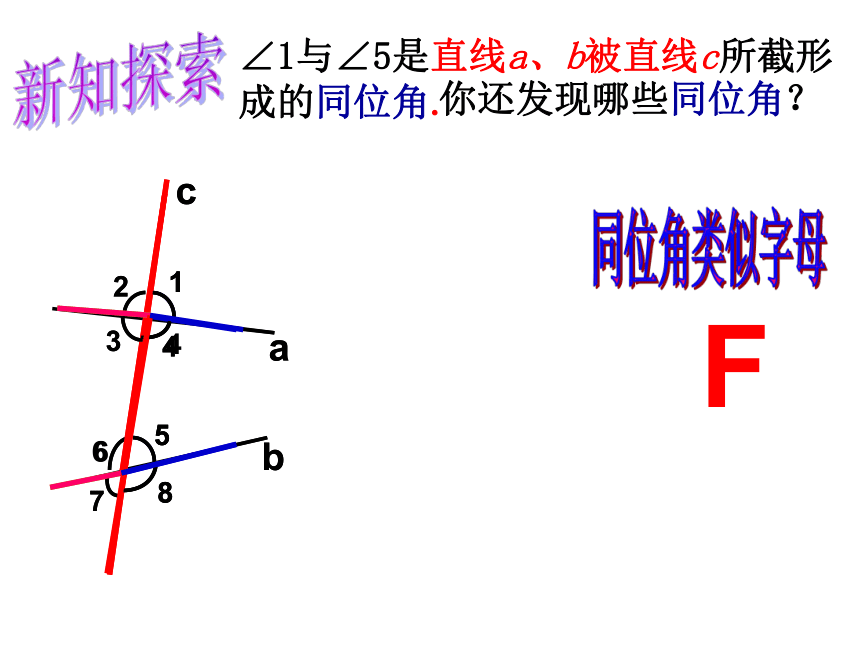
∠1与∠5是直线a、b被直线c所截形成的同位角.
1
4
5
8
b
a
c
2
1
4
3
6
5
8
7
b
a
c
1
5
2
6
3
7
4
8
F
你还发现哪些同位角？
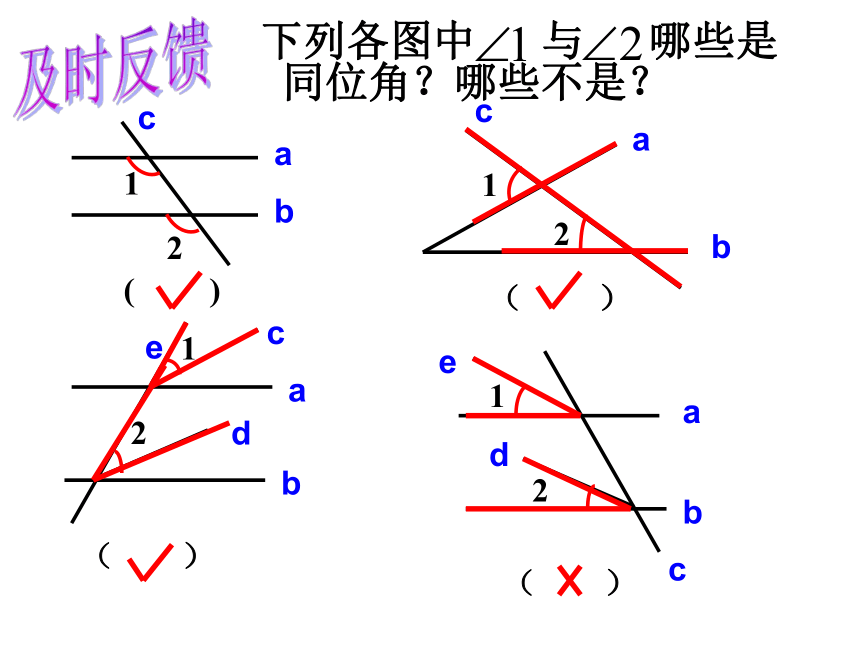
下列各图中 与 哪些是
同位角？哪些不是？
1
2
( )
1
2
（ ）
（ ）
1
2
（ ）
1
2
a
d
e
d
c
a
a
b
a
b
b
b
c
c
c
e
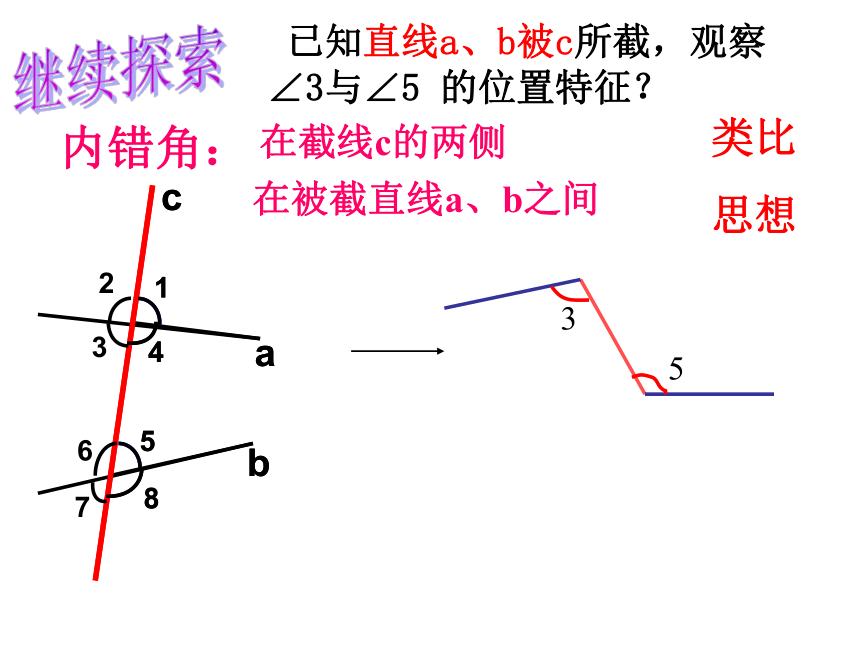
在被截直线a、b之间
在截线c的两侧
3
5
内错角：
1
4
5
8
b
a
c
2
1
4
3
6
5
8
7
b
a
c
已知直线a、b被c所截，观察∠3与∠5 的位置特征？
类比
思想
3
5
1
4
5
8
b
a
c
2
1
4
3
6
5
8
7
b
a
c
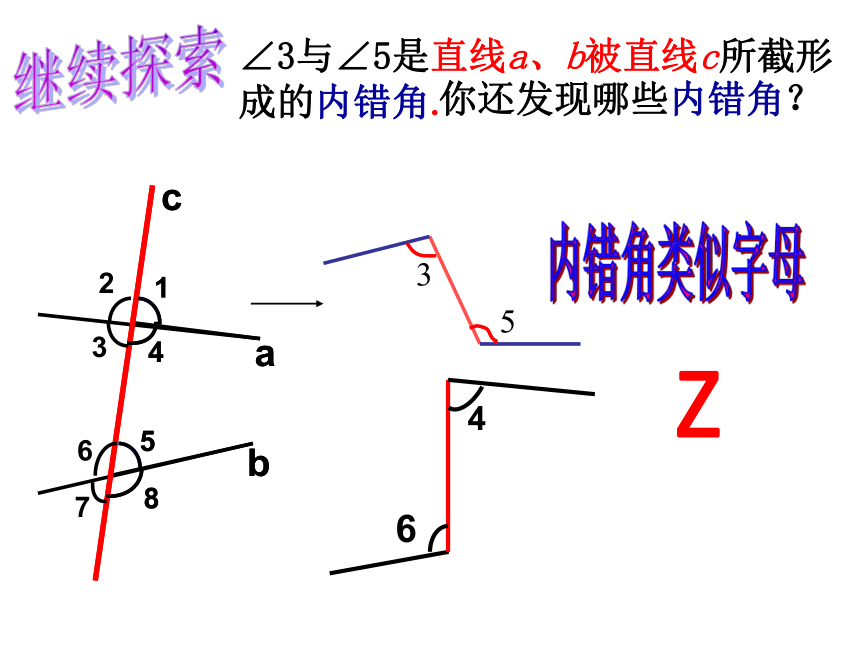
∠3与∠5是直线a、b被直线c所截形成的内错角.
你还发现哪些内错角？
4
6
Z
4
5
同旁内角：
1
4
5
8
b
a
c
2
1
4
3
6
5
8
7
b
a
c
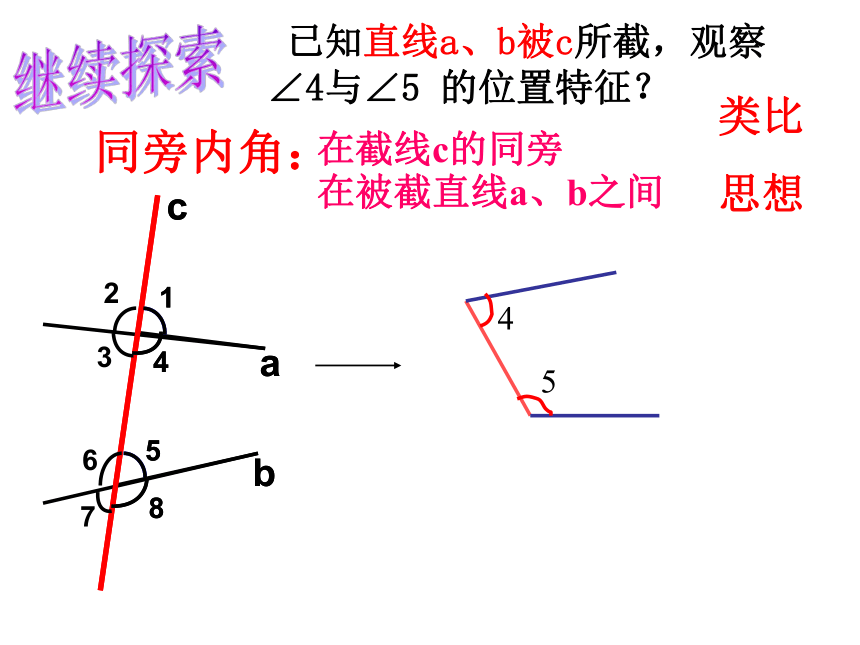
已知直线a、b被c所截，观察∠4与∠5 的位置特征？
在被截直线a、b之间
在截线c的同旁
类比
思想
∠4与∠5是直线a、b被直线c所截形成的同旁内角.
你还发现哪些同旁内角？
3
6
4
5
1
4
5
8
b
a
c
2
1
4
3
6
5
8
7
b
a
c
U
如图：直线a、b被直线 c所截构成的8个角中
同位角：∠1与∠5；
∠2与∠6；
∠4与∠8；
∠3与∠7.
内错角：∠3与∠5；
∠4与∠6.
同旁内角： ∠4与∠5；
∠3与∠6.
1
4
5
8
b
a
c
2
1
4
3
6
5
8
7
b
a
c
两条直线被第三条直线所截
同位角
同旁内角
内错角
梳理知识
类似字母
F
U
Z
2
1
基本图形
概念
截线同旁
被截线同侧
被截线之间
截线两侧
被截线之间
截线同旁
b
a
c
1
8
7
6
5
4
3
2
例1：已知直线a,b被c所截，指出所有的同位角、内错角、同旁内角.
b
a
1
8
7
6
5
4
3
2
9
变式1：已知直线a,c被直线b所截，∠9与∠1是一对什么关系的角？∠9与∠3呢？
3
1
9
分离基本图形法
直线a,c被直线b所截
注意：上述三类关系角类似于对顶角都是成对出现。不能说哪个角是同位角、内错角、同旁内角！
关键：要分清截线和被截线
∠9与∠1是内错角
∠9与∠3是同位角
变式2：∠9与∠2是哪两条线被哪一条线所截形成的一对什么角？∠9与∠6呢？
b
1
8
7
6
5
4
3
2
9
c
a
b
6
9
c
a
b
2
9
c
a
∠9与∠2是直线a、c被直线b所截形成的一对同旁内角
∠9与∠6是直线b、c被直线a所截形成的一对内错角
b
a
c
变式3：图中共有几对同位角？
按截线分类讨论：
共有12对
有4对
有4对
有4对
“手”可以千变万化，
能“变”出很多美妙的图形！
创造
如图：两只手的食指和拇指在同一平面内，它们构成的一对角可以看成是什么角 类似地，你还能用两只手的手指构成同位角和同旁内角吗
例2：如图，直线DE与BC被直线AB所截。
（1） 与 、 与 、 与 各是一对什么角？
E
D
C
B
A
1
2
3
4
（2）如果 相等，那么 和 相等吗？ 和 互补吗？请说明理由。
分别是内错角、同旁内角、同位角
A
B
O
C
D
E
2
1
如图，CD交AO于点E。若∠1= ∠2，
找出图中和 ∠2相等的角，以及和
∠ 2互补的角，并说明理由。
∵∠1＝∠2 （已知）
∠1＝∠AED （对顶角相等）
∴∠AED＝∠2
∵∠OED+∠AED=180°
∴∠AEC+∠2=180°
∠AED= ∠2, ∠OED+ ∠2=180°,
∠AEC+ ∠2=180°,理由如下:
解：
∴∠OED+ ∠2=180°,
∵∠OED=∠AEC
（对顶角相等）
如图，（1） 和 是直线_____与直线____被直线______所截形成的__________。
（2） 和 是直线_____与直线____被直线______所截形成的_________。
4
3
2
1
A
B
C
D
内错角
BD
BC
AD
BD
CD
AB
内错角
1
4
1
4
2
3
2
3
1
4
A
B
C
D
2
3
A
B
D
C
(1)
（2
课堂小结
知识
方法
体会
同位角、内错角、同旁内角的概念及在具体图形中识别方法
分类讨论、类比、分离基本图形等思想方法
数学与生活的密切联系
课后作业：
1、课时导航B: 第一页
2、利用3支笔，按要求先摆出图形，在画出图形。
（1）恰好有4对同位角；
（2）恰好有4对内错角
（3）恰好有6对同旁内角；