1.3平行线的判定

课件24张PPT。1.3 (1)平行线的判定教学目标:1.发现:同位角相等,两直线平行2.掌握平行线的判定方法:同位角相等,两直线平行

会用并会简单的推理和表述
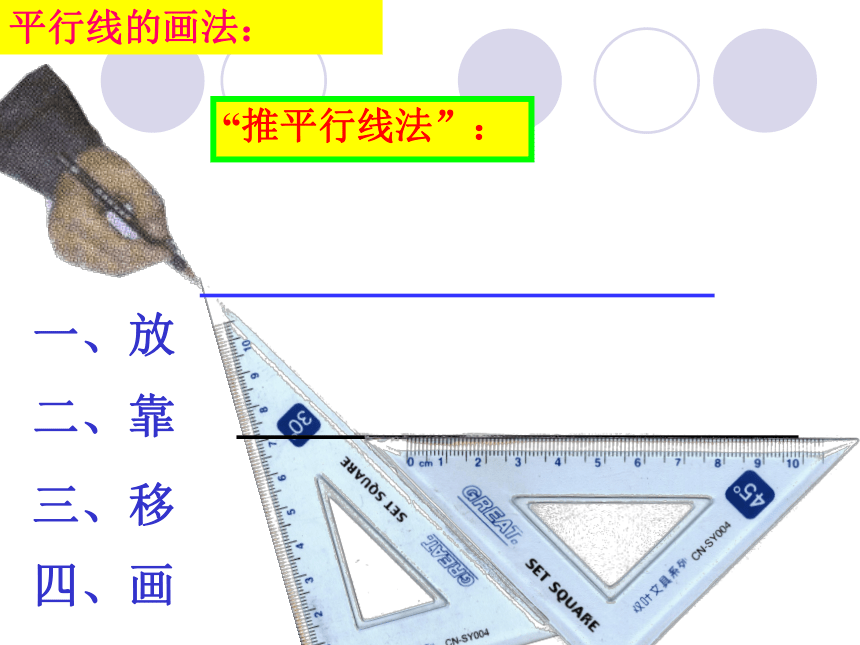
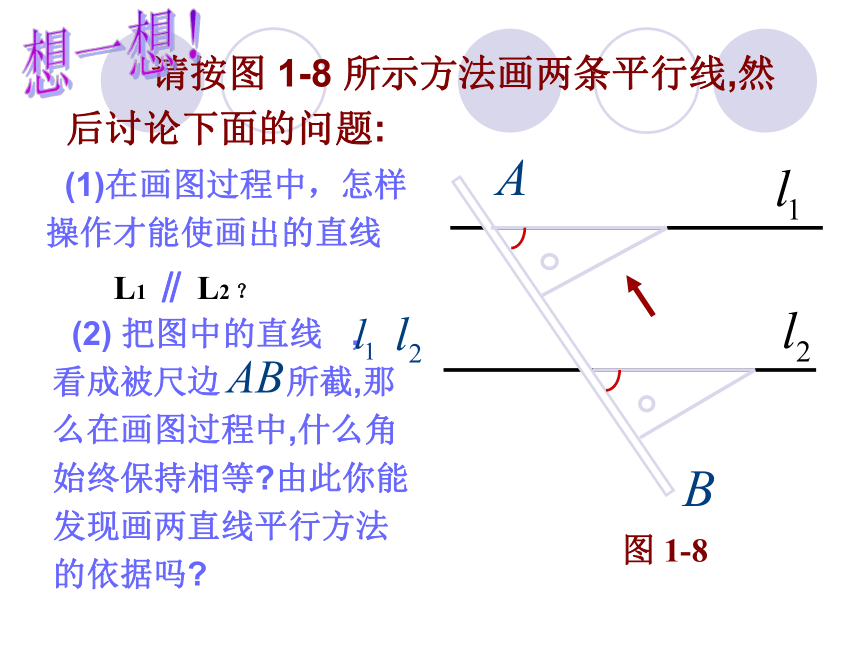
重点:平行线的判定方法:同位角相等,两直线平行难点:例1中简单的推理和表述一、放二、靠三、移四、画平行线的画法：“推平行线法”： 请按图 1-8 所示方法画两条平行线,然后讨论下面的问题: (1)在画图过程中，怎样操作才能使画出的直线 (2) 把图中的直线 , 看成被尺边 所截,那么在画图过程中,什么角始终保持相等?由此你能发现画两直线平行方法的依据吗?想一想！图 1-8L1 ∥ L2 ？ 人们在长期实践中总结以下基本事实: 两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行.平行线判定方法1：
同位角相等,两直线平行。请记住！平行线的判定方法1 两条直线被第三条直线所截，如果同位角相等，那么这两 条直线平行。简单地说：同位角相等，两直线平行。L1 L2 12符号表示：∵∠1＝∠2
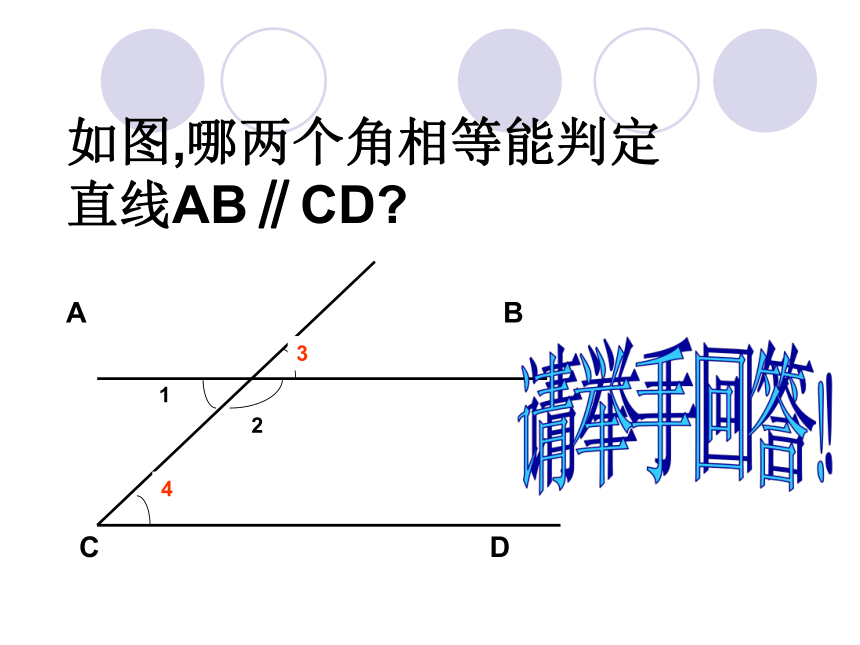
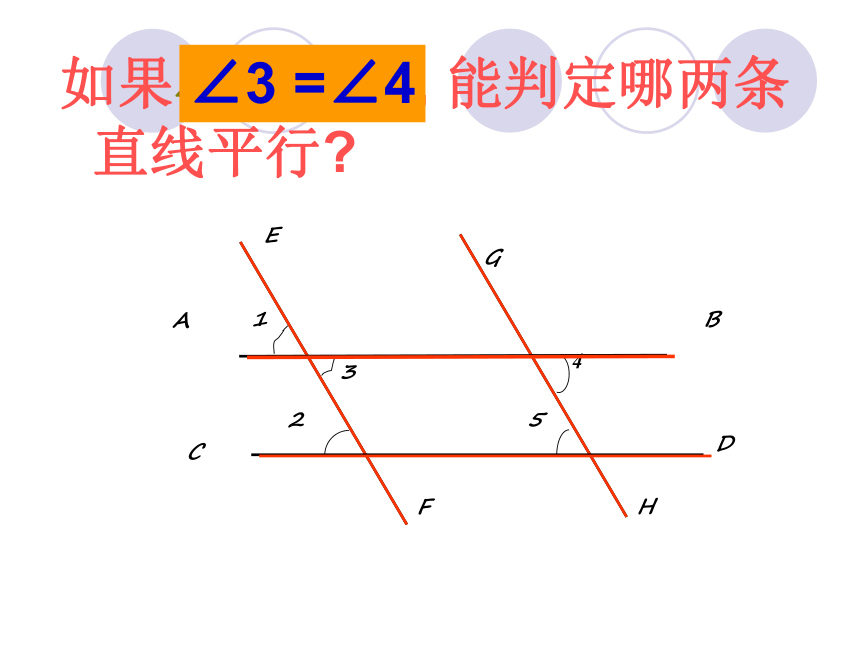
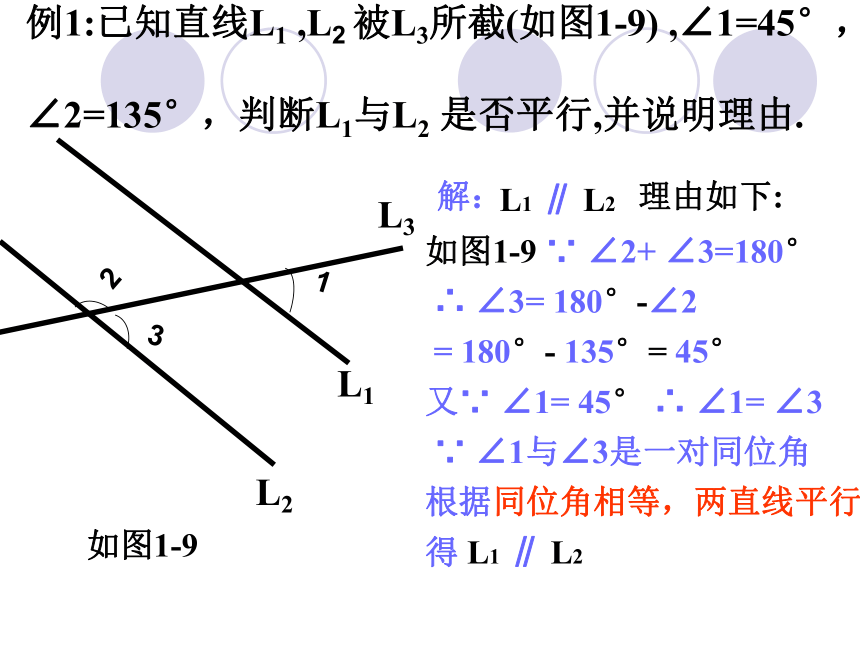
∴L1∥L2 新课讲解如图,哪两个角相等能判定直线AB∥CD?1432ADCB请举手回答！4123ABCEFD5HG∠3 =∠4例1:已知直线L1 ,L2 被L3所截(如图1-9) ,∠1=45°，

∠2=135°，判断L1与L2 是否平行,并说明理由.　 L1L2L3 解： 理由如下:
如图1-9 ∵ ∠2+ ∠3=180°
∴ ∠3= 180°-∠2
= 180°- 135°= 45°
又∵ ∠1= 45° ∴ ∠1= ∠3
∵ ∠1与∠3是一对同位角
根据同位角相等，两直线平行
得 L1 ∥ L2
如图1-9L1 ∥ L2 已知直线 AB、CD被EF所截
(如图) ,
判断 AB与CD是否平行,并说
明理由.
　 变式1已知直线 AB、CD被EF所截
(如图) ,
判断 AB与CD是否平行,并说
明理由.
　 变式2∠1＝∠4若 AB⊥EF，CD⊥EF则 AB∥ CD 垂直于同一条直线的两条直线互相平行∵∴在同一平面内，这也是平行线判定方法应用于生活!为什么每只皮划艇都沿着垂直于终点线的方向行驶，就能保证航线互相平行？
课内练习1、如图，∠1 = ∠2 = 55°， ∠3等于多少度？
直线AB、CD平行吗？ 说明你的理由。312ABFCDE∵ ∠1 = ∠2 = 55° ∠3 = ∠2， ∴ ∠3 =∠1= 55° ∴ AB∥CD. 随堂练习（ ）对顶角相等(同位角相等,两直线平行) 某人骑自行车从Ａ地出发，沿正东方向前进至Ｂ处后，右转１５°，沿直线向前行驶到Ｃ处。（如图）这时他想仍按正东方向行驶，那么他应怎样调整行驶方向？请画出他应继续行驶的路线，并说明理由。Ｃ2.亲手画一画—课内练习2
你学到了什么？ 你还有什么困惑吗？你有什么经验与收获让同学们共享呢？课堂小结（1）、两种平行线的判定方法（2）判定两直线平行的关键步骤：一找同位角，二说明同位角相等
（3）注意说理过程的严密性
（4）体会数学来源于生活，又应用于生活的用数学的思想课堂小结作业： 1、复习、整理、巩固今天所学知识 . (当天巩固)
2、作业本(1)1.3(1)基础练习必做,希望完成综合运用.(当天上交)
3、课课练A1.3(1)课后作业必做,当堂训练选做. (回家作业)
4、预习下一节课,选做课本作业题 (回家作业)
1.已知：如图，∠1和∠2是直线a、b被直线c截出的同旁内角，且∠1+∠2= 求证：a∥b拓展提高2.已知：如图，∠1和∠2是直线a、b被直线c截出的内错角，且∠1=∠2
求证：a∥b拓展提高C易错题集1.如图，直线AB//CD,直线EF,GH分别与AB,CD相交,所形成同位角的对数共有（ ）D.36对C.32对B.16对A.8对2、如图,平行直线AB、CD与相交直线EF 、GH相交,图中的同旁内角共有( )对
A 4对 B 8对 C 12 对 D 16对C∠1和∠2不是同位角3.请判断：如图中的∠1和∠2是同位角吗? 为什么?∠1和∠2是同位角，再见下课，再见！