§1.1平行线

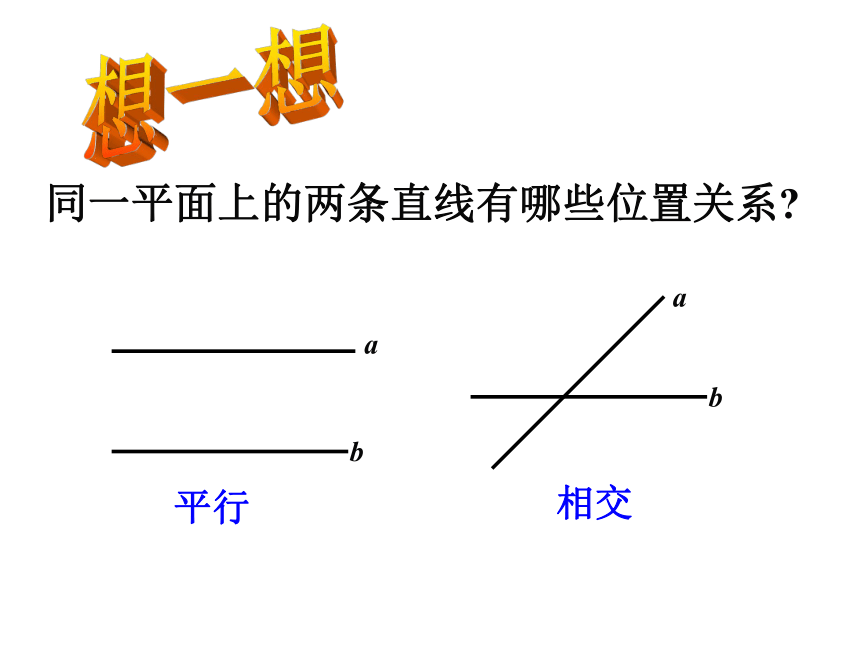
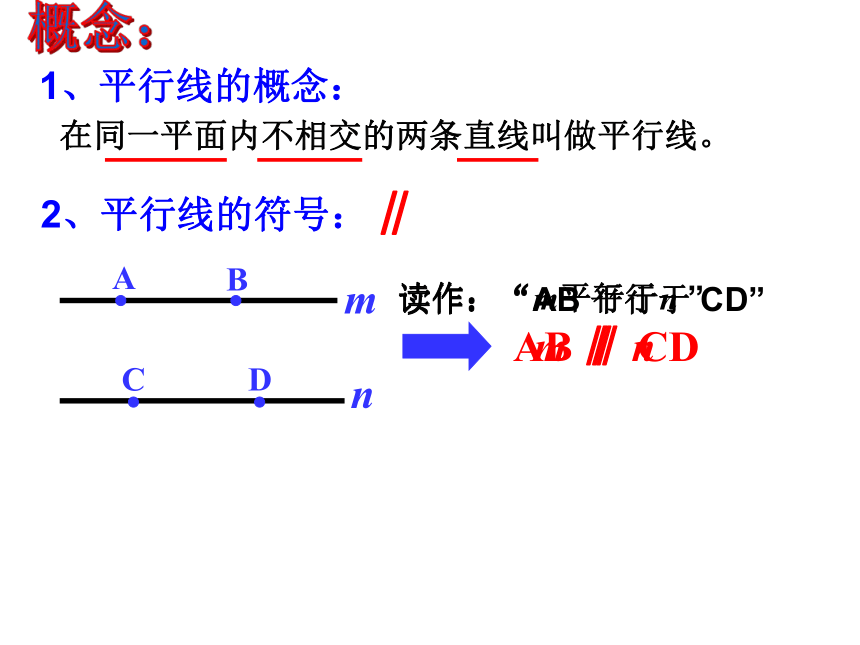
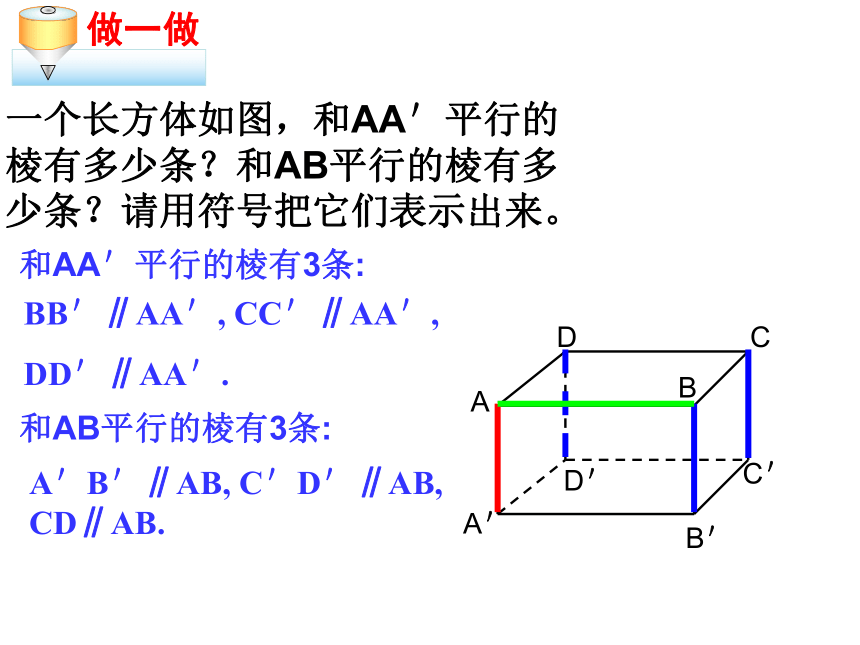
课件28张PPT。§1.1 平行线荷兰国旗俄罗斯国旗阿根廷国旗比利时国旗数学来源于生活很多国家的国旗上都有平行线跑道屏风同一平面上的两条直线有哪些位置关系?平行相交想一想C DBA1、平行线的概念：在同一平面内不相交的两条直线叫做平行线。2、平行线的符号：∥AB ∥ CD读作：“AB 平行于 CD”　读作：“m平行于n ” 　mnm ∥ n概念：一个长方体如图，和AA＇平行的棱有多少条？和AB平行的棱有多少条？请用符号把它们表示出来。和AA＇平行的棱有3条:BB＇∥AA＇, CC＇∥AA＇,
DD＇∥AA＇.和AB平行的棱有3条:A＇B＇∥AB, C＇D＇∥AB,
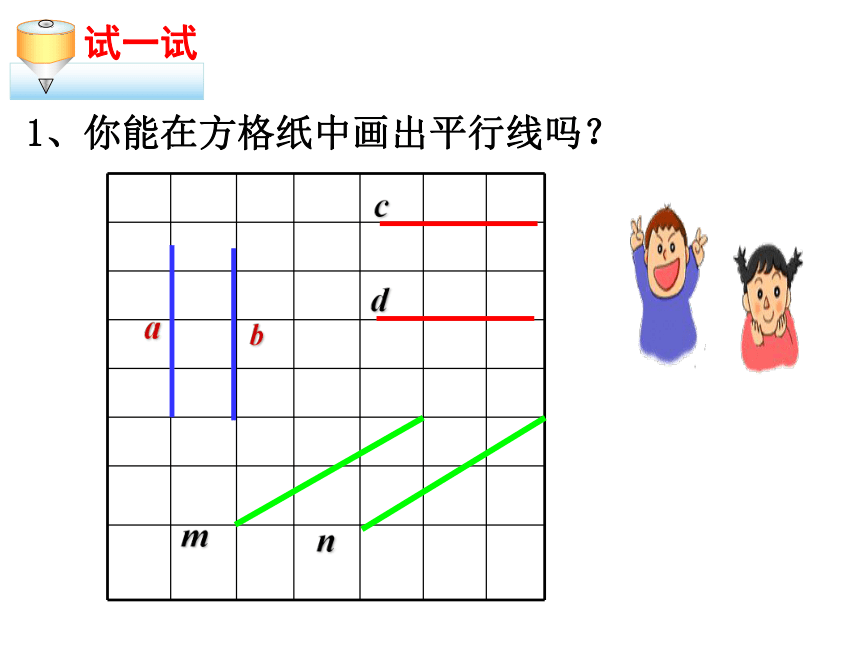
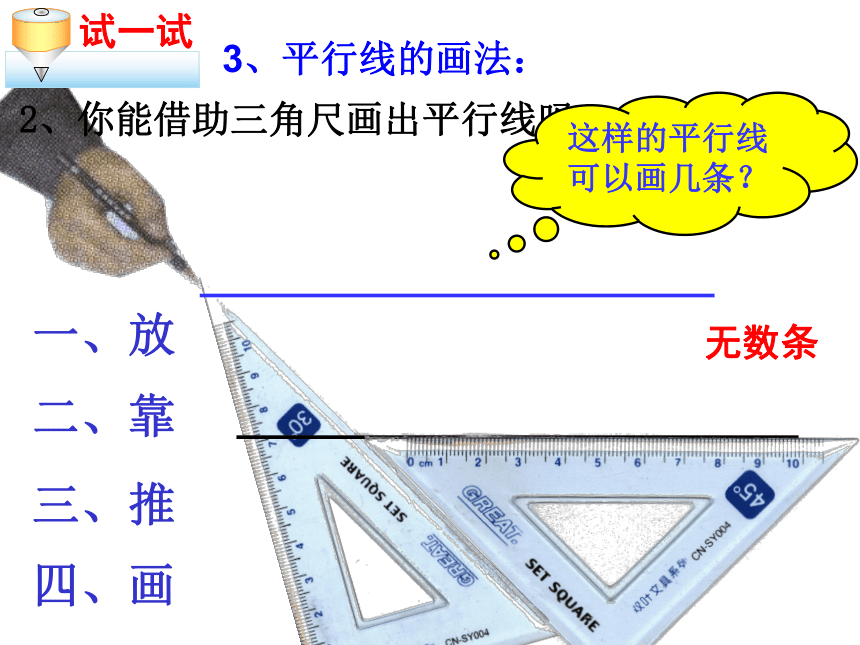
CD∥AB.1、你能在方格纸中画出平行线吗？一、放二、靠三、推四、画2、你能借助三角尺画出平行线吗？ 3、平行线的画法：这样的平行线可以画几条？无数条AB.C⑴给你一条直线AB，及直线外一点C，过点C画出直线AB的平行线。这样的平行线可以画几条？1条⑵再给你直线外一点D，过点D画出直线AB的平行线。.D你所画的两条直线会互相平行吗？会动手实践过直线ＡＢ外一点Ｐ作直线ＡＢ的平行线，看看你能作出吗？能作出几条？· A B P4、一般地,平行线有以下的基本事实： 经过直线外一点，有且只有一条直线与这条直线平行。结论：说明：人们在长期实践中总结出来的结论叫基本事实，也称为公理，它可以作为以后推理的依据．5、看书本例题1、判断：
⑴不相交的两条直线叫做平行线。 （ ）
⑵在同一平面内不相交的两条线段叫平行线。（ ）⑸过一点有且只有一条直线与已知直线平行。（ ）⑶在同一平面内不相交的两条直线叫平行线。（ ）×××√2、选择：
在同一平面内有三条直线，它们的交点个数是（ ）
A.0或2 B.0或3 C.0或1 D.0或1或2或3
D⑷与已知直线平行的直线有且只有一条。 ( )×（1）用符号表示下面两棱的位置关系：
A1B1___AB，AA1____AB ，A1D1____C1D1，AD___BC。（2）A1B1与BC所在的直线是两条不相交的直线，它们＿＿＿＿＿平行线（填“是”或“不是”），由此可知，在＿＿ ＿＿内，两条不相交的直线才能叫平行线。3、∥⊥⊥∥不是同一平面根据下列语句，画出图形：（1）过△ABC的顶点C，画MN∥AB；
（2）过△ABC的边AB的中点D，画平行于AC的直线，交BC于点E。4、MNDE5、如图，点O是直线CD外一点，OA∥CD，OB∥CD，那么∠AOB是平角，为什么？·ABC DO解：∵OA∥CD，OB∥CD即 点A、O、B在同一条直线上∴ ∠AOB是平角∴OA、OB表示同一条直线（经过直线外一点，有且只有一条直线与已知直线平行） 本节课你的收获是什么？(1)什么是平行线； (3)平行线的画法; (2)平行线的表示方法;(4)平行的基本事实（5）在同一平面内两条直线有几种位置关系？小结作业: ① 复习、整理、巩固今天所学知识.
书上A组做在书本上; B组供有能力的同学选做.
② 作业本① 1.1完成 . (当天上 交)试一试1、下列语句中，正确的个数是 （ ）
（1）不相交的两条直线是平行线
（2）同一平面内，两直线的位置关系有两种，即相交或平行
（3）若线段AB与CD没有交点则AB//CD
（4）若a//b,b//c,则a 与c不相交
（A)1个 （B）2个 （C）3个 （D）4个B经过直线外一点，有且只有一条直线与已知直线平行。３、下列说法正确的是（　　　）
Ａ、一条直线的平行线有且只有一条
Ｂ、经过一点有且只有一条直线与已知直线平行
Ｃ、经过一点有两条直线与某一直线平行
Ｄ、过直线外一点有且只有一条直线与已知直线平行
Ｄ4、如图，长方体的各棱中，与AＡ１平行的条数有（　　）
Ａ、１　　Ｂ、２　　　　Ｃ、３　　　Ｄ、４Ｃ5、如果两根铁轨不保持平行，会有什么现象发生? 7、在平面上有三条直线a , b , c ,
它们之间可能有哪几种位置关系？请画
图说明。（提示：从交点的个数考虑）
　同一平面内，三条直线的交点可以有　　　　　　　个．０或１或２或３　8、如图所示，已知点A和点B分别在直线l外和l上，（1）过点A画出下列各图形： ①过点B，作直线AB； ②垂直于直线l的直线； ③平行于直线l的直线；（2）过点B画出下列各图形：
①垂直于直线l的直线；
②平行于直线l的直线；（3）从上述两小题，你体会到“平行公理”与“垂线的性质”之间有何区别？ 9、 在同一平面内有 4 条直线，这 4 条直线可以把这个平面分成几部分？ (2) 当 4 条直线中只有三条直线两两平行时，可以把平面分成 8 部分. (3) 当 4 条直线仅有两条直线互相平行时，可以把整个平面分成 9 部分或 10 部分. (4) 当 4 条直线中有两条直线平行，另两条直线也平行时，可以把平面分成 9 部分. (5) 当 4 条直线任意两条都不平行时，可以把平面
分成 8 部分, 或 10 部分, 或 11 部分.再见再见