1.4平行线的性质(2)

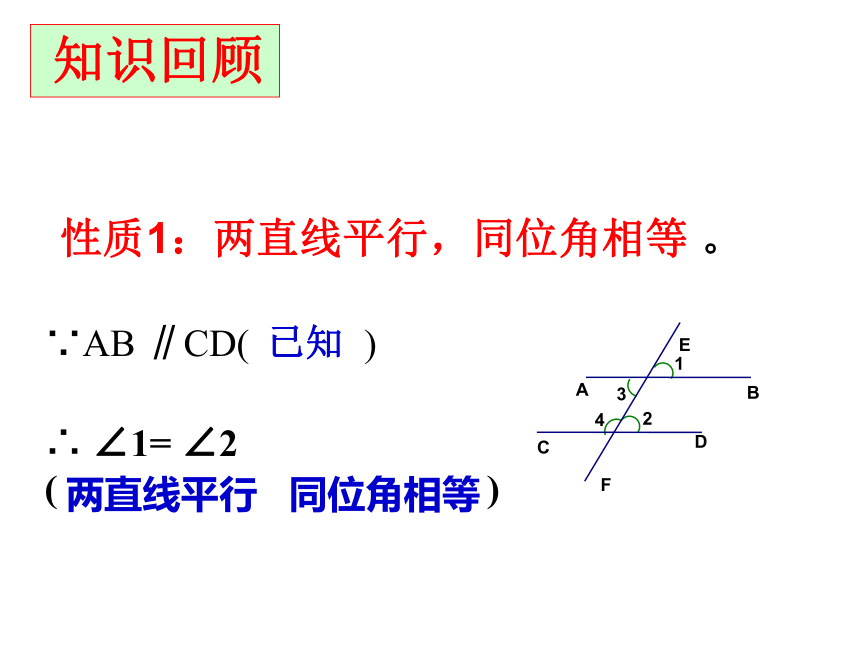
课件13张PPT。1.4平行线的性质(2) 知识回顾性质1：两直线平行，同位角相等 。∵AB ∥CD( )已知∴ ∠1= ∠2
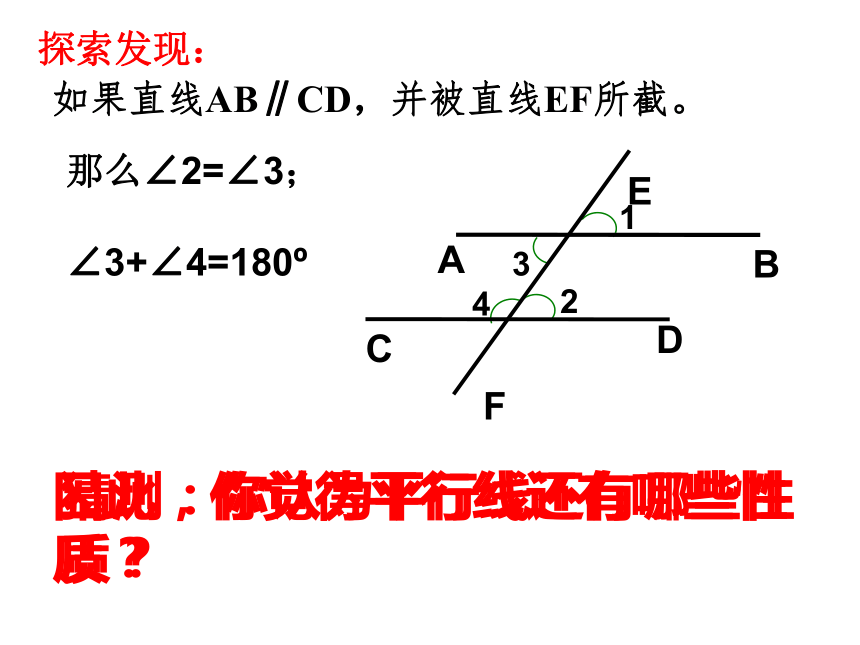
( )两直线平行 同位角相等因此，你觉得平行线还有哪些性质？ 如果直线AB∥CD，并被直线EF所截。探索发现：猜测：你认为平行线还有哪些性质？ 那么∠2=∠3；
∠3+∠4=180o平行线的性质2：
两条平行线被第三条直线所截，内错角相等。
简单地说，两直线平行，内错角相等。两条平行线被第三条直线所截，同旁内角互补。
简单地说，两直线平行，同旁内角互补。∵AB ∥CD( )∴ ∠1= ∠2
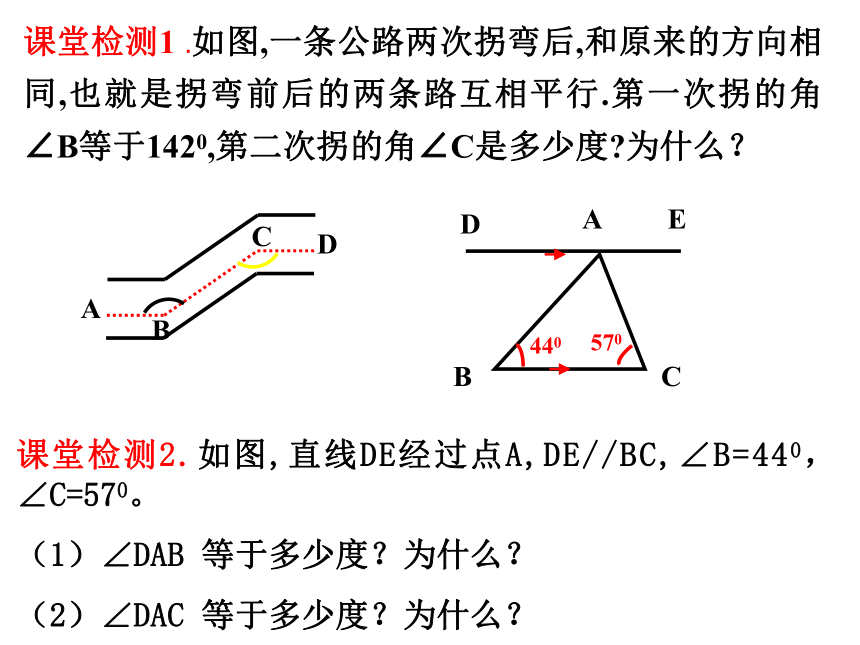
( )已知两直线平行，内错角相等∵AB ∥CD( )已知∴ ∠1+ ∠3=180o（ ）两直线平行，同旁内角互补课堂检测1 .如图,一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角∠B等于1420,第二次拐的角∠C是多少度?为什么？课堂检测2.如图,直线DE经过点A,DE//BC,∠B=440，∠C=570。
（1）∠DAB 等于多少度？为什么？
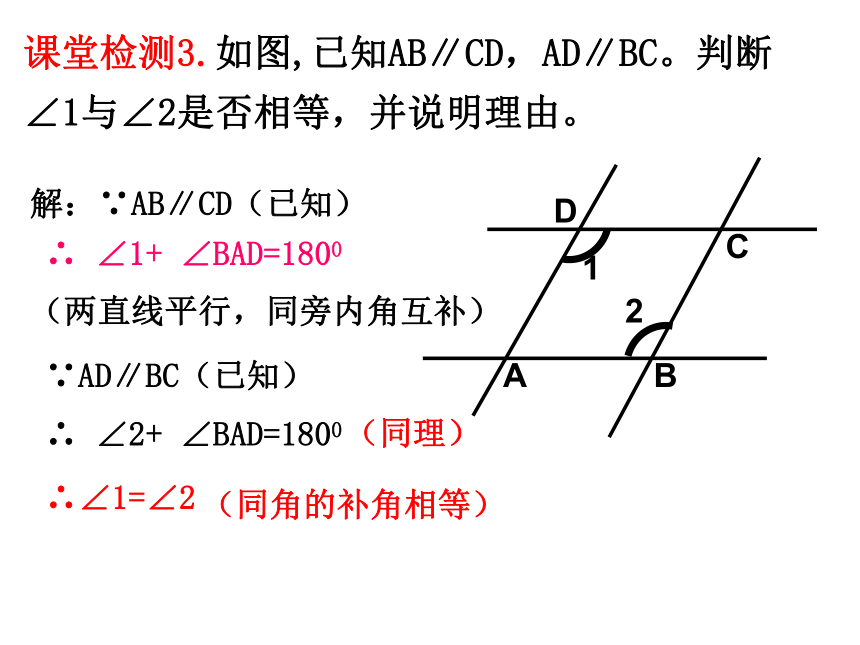
（2）∠DAC 等于多少度？为什么？课堂检测3.如图,已知AB∥CD，AD∥BC。判断∠1与∠2是否相等，并说明理由。ABCD12解：∵AB∥CD（已知）∴ ∠1+ ∠BAD=1800（两直线平行，同旁内角互补）∴∠1=∠2（同角的补角相等）∵AD∥BC（已知）∴ ∠2+ ∠BAD=1800（同理）课堂检测4.如图,已知∠ABC+∠C=180°,BD平分∠ABC。∠CBD与∠D相等吗？请说明理由。ABDC解：∠CBD=∠D。理由如下：∵∠ABC+∠C=1800（已知）∴AB∥CD
（同旁内角互补，两直线平行）∴∠D=∠ABD
（两直线平行，内错角相等）又∵BD平分∠ABC∴∠CBD=∠ABD=∠D小结：判定和性质的比较两条平行直线被第三条直线直线所截，互换。2、判定是已知 推出 ；角的相等或互补两直线平行 性质是已知 ，说明 。两直线平行角的相等或互补 1、如图所示 ∠1 =∠2，求证 ： ∠3 =∠4证明：∵ ∠1 =∠2（已知） ∴a//b
(同位角相等,两直线平行) ∴ ∠3 =∠4
(两直线平行，内错角相等)练一练：练一练：2、如图1,已知AD∥BC，∠BAD=∠BCD。
判断AB与CD是否平行,并说明理由3、如图，CD是△ABC的中线，延长CD至E，使CD=DE.试判断AC与BE是否平行，并说明理由. 4、已知如图，AD⊥BC于D，EG⊥BC于G，∠E=∠3，试说明∠1=∠2的理由。 　　　　 课堂小结：这节课你有什么收获？