浙教版七年级下册4.1 因式分解课件(共20张PPT)
文档属性
| 名称 | 浙教版七年级下册4.1 因式分解课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 196.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 00:00:00 | ||
图片预览




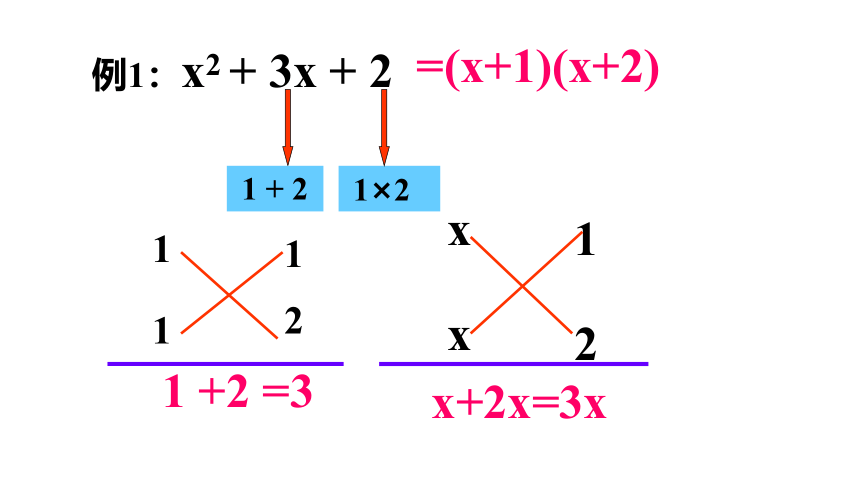



文档简介
(共20张PPT)
第四章:因式分解
-------十字相乘法
计算:
(1) (x+2)(x+1)
(2) (x+2)(x-1)
(3) (x-2)(x-1)
(4) (x+2)(x+3)
(x+p)(x+q)
x2+(p+q)x+pq
一般地,
=x2+3x+2
=X2+x-2
=x2+5x+6
=x2-3x+2
=x2+(p+q)x+pq
= (x+p)(x+q)
夯实基础,稳扎稳打
十字相乘法:
对于二次三项式的分解因式,借用一个十字叉帮助我们分解因式,这种方法叫做十字相乘法。
即:x2 +(p+q)x+pq=(x+p)(x+q)
x
x
p
q
px+qx=(p+q)x
x2
pq
1.十字相乘法因式分解的步骤:
①竖分二次项与常数项;
②交叉相乘,求代数和,
使和等于一次项;
③检验确定,横写因式。
十字相乘法
顺口溜:
竖分常数交叉验,
横写因式不能乱。
x2+(p+q)x+pq=
x
x
p
q
px+qx=(p+q)x
∴x2+(p+q)x+pq
=(x+p)(x+q)
例1:x2 + 3x + 2
1 + 2
1×2
1
1
1
2
1 +2 =3
x
x
1
2
x+2x=3x
=(x+1)(x+2)
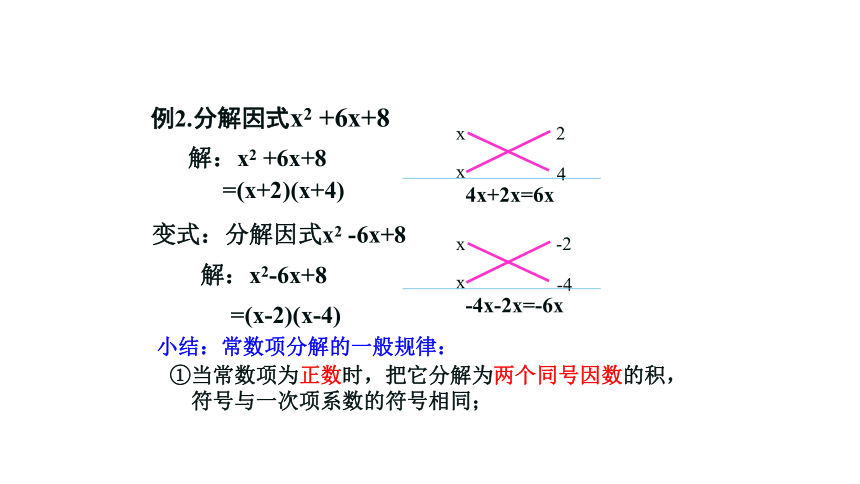
例2.分解因式x2 +6x+8
=(x+2)(x+4)
x
x
2
4
4x+2x=6x
解:x2 +6x+8
变式:分解因式x2 -6x+8
解:x2-6x+8
=(x-2)(x-4)
x
x
-2
-4
-4x-2x=-6x
小结:常数项分解的一般规律:
①当常数项为正数时,把它分解为两个同号因数的积,
符号与一次项系数的符号相同;
=(x-12)(x+5)
x
x
-12
5
-12x+5x=-7x
解:x2 -7x-60
变式:分解因式x2 +7x-60
解:x2+7x-60
=(x+12)(x-5)
x
x
12
-5
12x-5x=7x
小结:常数项分解的一般规律:
②当常数项为负数时,把它分解为两个异号因数的积,
其中绝对值较大的因数的符号与一次项系数的符号相同;
例3.分解因式x2 -7x-60
1
1
1
1
对于二次项系数为1的二次三项式分解的方法是“拆常数项,凑一次项”
小结:
我想试一试------自古成功在尝试
我想试一试------自古成功在尝试
在每一时每一刻,不管你在做什么事情,也不管这件事是简单还是困难,都要带着勇气去试一试。试一试了,即使失败,也能吸取教训,在下一次取得成功。但如果连试一试都不敢,那你就连成功的机会都灰飞烟灭了。
竖分常数交叉验:
重要的,我想试一试-----分解因式练习一:
横写相乘不能乱
(二次项系数不为一):重要的,尝试
分别分解为两数相乘
①2x7+4x(-5)=-6不成立
二次项系数
一次项系数
常数项
8
6
-35
②2x(-7)+4x5=6成立
-7
7
-5
4
2
5
8x2+6x-35=(2x+5)(4x-7)
例6.
连续递推,豁然开朗
例7 分解因式 3x -10x+3
2
解:3x -10x+3
2
x
3x
-3
-1
-9x-x=-10x
=(x-3)(3x-1)
例8 分解因式 5x -17x-12
2
解:5x -17x-12
2
5x
x
+3
-4
-20x+3x=-17x
=(5x+3)(x-4)
例9:把下列二次三项式分解因式:
(1)12x2-5x-2 (2) 5x2+6xy-8y2
(1)12x2-5x-2
=(3x-2)(4x+1)
(2)5x2+6xy-8y2
x
5x
+2y
-4y
=(x+2y)(5x-4y)
-2
+1
3x
4x
3x·1+4x·(-2)=-5x
x·(-4y)+5x·2y=-4xy+10xy=6xy
练习二:重要的,希望就在前方
分解下列因式:
(1)2x2-5x-3
(2)3x2+8x-3
小结:
对于二次项系数不是1的二次三项式分解的方法是“拆两头,凑中间”
=(2x+1)(x-3)
=(3x-1)(x+3)
例10 把 分解因式
分析: 当二次项系数为负时,二次项系数分解的两个因数异号, 则十字辅助图的各种可能性就会更多.因此应先把负号提到 括号外面.
解:
用十字相乘法,把 因式分解得
1
3
-2
-1
分析:第三项和第一项一样,先把系数十字分解,最后加上字母.
1
5
-1
-6
例11:把5x2-11xy+6y2分解因式
5x2-11xy+6y2
思维拓展,更上一层
例12. 10(x +2)2 -29(x+2) +10
答案 (2x-1)(5x+8)
练习三:将下列各式分解因式
1、 7x -13x+6
2
2、 -y -4y+12
2
3、 15x +7xy-4y
2
2
4、 10(x +2) -29(x+2) +10
2
答案(7x+6)(x+1)
5、 x -(a+1) x+a
2
答案- (y+6)(y-2)
答案 (3x-y)(5x+4y)
答案 (2x-1)(5x+8)
答案 (x-1)(x-a)
总结
十字相乘法分解因式的步骤:
1 竖分二次项与常数项。
2 交叉相乘并相加。
3 检验确定,横写因式。
本节课你有什么收获?
第四章:因式分解
-------十字相乘法
计算:
(1) (x+2)(x+1)
(2) (x+2)(x-1)
(3) (x-2)(x-1)
(4) (x+2)(x+3)
(x+p)(x+q)
x2+(p+q)x+pq
一般地,
=x2+3x+2
=X2+x-2
=x2+5x+6
=x2-3x+2
=x2+(p+q)x+pq
= (x+p)(x+q)
夯实基础,稳扎稳打
十字相乘法:
对于二次三项式的分解因式,借用一个十字叉帮助我们分解因式,这种方法叫做十字相乘法。
即:x2 +(p+q)x+pq=(x+p)(x+q)
x
x
p
q
px+qx=(p+q)x
x2
pq
1.十字相乘法因式分解的步骤:
①竖分二次项与常数项;
②交叉相乘,求代数和,
使和等于一次项;
③检验确定,横写因式。
十字相乘法
顺口溜:
竖分常数交叉验,
横写因式不能乱。
x2+(p+q)x+pq=
x
x
p
q
px+qx=(p+q)x
∴x2+(p+q)x+pq
=(x+p)(x+q)
例1:x2 + 3x + 2
1 + 2
1×2
1
1
1
2
1 +2 =3
x
x
1
2
x+2x=3x
=(x+1)(x+2)
例2.分解因式x2 +6x+8
=(x+2)(x+4)
x
x
2
4
4x+2x=6x
解:x2 +6x+8
变式:分解因式x2 -6x+8
解:x2-6x+8
=(x-2)(x-4)
x
x
-2
-4
-4x-2x=-6x
小结:常数项分解的一般规律:
①当常数项为正数时,把它分解为两个同号因数的积,
符号与一次项系数的符号相同;
=(x-12)(x+5)
x
x
-12
5
-12x+5x=-7x
解:x2 -7x-60
变式:分解因式x2 +7x-60
解:x2+7x-60
=(x+12)(x-5)
x
x
12
-5
12x-5x=7x
小结:常数项分解的一般规律:
②当常数项为负数时,把它分解为两个异号因数的积,
其中绝对值较大的因数的符号与一次项系数的符号相同;
例3.分解因式x2 -7x-60
1
1
1
1
对于二次项系数为1的二次三项式分解的方法是“拆常数项,凑一次项”
小结:
我想试一试------自古成功在尝试
我想试一试------自古成功在尝试
在每一时每一刻,不管你在做什么事情,也不管这件事是简单还是困难,都要带着勇气去试一试。试一试了,即使失败,也能吸取教训,在下一次取得成功。但如果连试一试都不敢,那你就连成功的机会都灰飞烟灭了。
竖分常数交叉验:
重要的,我想试一试-----分解因式练习一:
横写相乘不能乱
(二次项系数不为一):重要的,尝试
分别分解为两数相乘
①2x7+4x(-5)=-6不成立
二次项系数
一次项系数
常数项
8
6
-35
②2x(-7)+4x5=6成立
-7
7
-5
4
2
5
8x2+6x-35=(2x+5)(4x-7)
例6.
连续递推,豁然开朗
例7 分解因式 3x -10x+3
2
解:3x -10x+3
2
x
3x
-3
-1
-9x-x=-10x
=(x-3)(3x-1)
例8 分解因式 5x -17x-12
2
解:5x -17x-12
2
5x
x
+3
-4
-20x+3x=-17x
=(5x+3)(x-4)
例9:把下列二次三项式分解因式:
(1)12x2-5x-2 (2) 5x2+6xy-8y2
(1)12x2-5x-2
=(3x-2)(4x+1)
(2)5x2+6xy-8y2
x
5x
+2y
-4y
=(x+2y)(5x-4y)
-2
+1
3x
4x
3x·1+4x·(-2)=-5x
x·(-4y)+5x·2y=-4xy+10xy=6xy
练习二:重要的,希望就在前方
分解下列因式:
(1)2x2-5x-3
(2)3x2+8x-3
小结:
对于二次项系数不是1的二次三项式分解的方法是“拆两头,凑中间”
=(2x+1)(x-3)
=(3x-1)(x+3)
例10 把 分解因式
分析: 当二次项系数为负时,二次项系数分解的两个因数异号, 则十字辅助图的各种可能性就会更多.因此应先把负号提到 括号外面.
解:
用十字相乘法,把 因式分解得
1
3
-2
-1
分析:第三项和第一项一样,先把系数十字分解,最后加上字母.
1
5
-1
-6
例11:把5x2-11xy+6y2分解因式
5x2-11xy+6y2
思维拓展,更上一层
例12. 10(x +2)2 -29(x+2) +10
答案 (2x-1)(5x+8)
练习三:将下列各式分解因式
1、 7x -13x+6
2
2、 -y -4y+12
2
3、 15x +7xy-4y
2
2
4、 10(x +2) -29(x+2) +10
2
答案(7x+6)(x+1)
5、 x -(a+1) x+a
2
答案- (y+6)(y-2)
答案 (3x-y)(5x+4y)
答案 (2x-1)(5x+8)
答案 (x-1)(x-a)
总结
十字相乘法分解因式的步骤:
1 竖分二次项与常数项。
2 交叉相乘并相加。
3 检验确定,横写因式。
本节课你有什么收获?
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
