2.2.2二元一次方程组的解法--加减消元法
文档属性
| 名称 | 2.2.2二元一次方程组的解法--加减消元法 |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-13 22:10:52 | ||
图片预览











文档简介
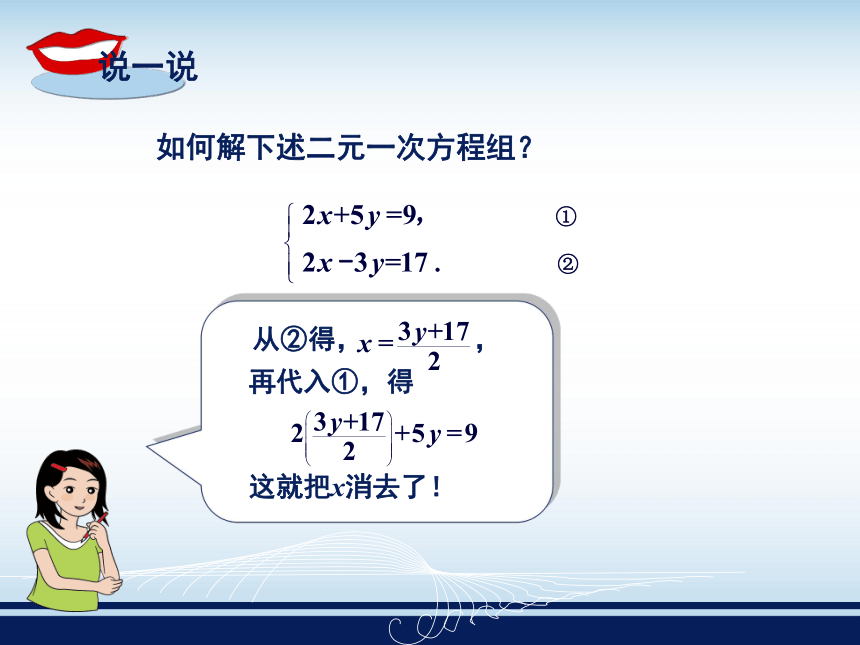
课件33张PPT。二元一次方程组的解法2.2——2.2.2 加减消元法 如何解下述二元一次方程组?从②得, ,
再代入①,得
这就把x消去了!她得到的y的方程也就是
(3y+17)+5y=9
这不就可以直接从②得,
2x=3y+17,
然后把它代入①吗? 还有没有更简单的解法呢? 方程①和②中都有2x,
为了消去x,干脆把方程①减去方程②就可以了!①-②,得 8y= -8,
解得 y= -1
把y=-1代入①,得
2x+5(-1)=9,
解得 x= 7
因此原方程组的一个解是例3 解方程组:举
例 9x = 9. 解得 x = 1把x=1代入① ,得
7×1+3y = 1因此原方程组的一个解是7x+3y+(2x-3y)=1+8解得 y = -2 两个方程中的未知数y的系数互为相反数,可以消去y. 在上面的两个方程组中,把方程①减去②,或
者把方程①与②相加,便消去了一个未知数,被消
去的未知数的系数有什么特点? 被消去的未知数系数相等或互为相反数. 如何较简便地解下述二元一次方程组? 要是①、②两式中,x的系数相等或者互为相反数就好办了! 把①式两边乘以3,不就行了么!解 ①×3,得 6x+9y=-33 ③ ②-③,得 -14y = 42解得 y= -3把y =-3代入①,得
2x+3×(-3)= -11,解得 x= -1因此原方程组的一个解是例4 解方程组:举
例 能不能使两个方程中x(或y)的系数相等(或互为相反数)呢?解得 y = 5把y=5代入①,得 3x+4×5=8因此原方程组的一个解是将两个方程中的x的系数变为相等.解得 x = -4②×3 ,得
12x+9y=-3. ④③-④ ,得 7y=35. 上面四个方程组中,是如何消去一个未知数的? 消去一个未知数的方法是:如果两个方程中有一个未知数的系数相等(或互为相反数),那么把这两个方程相减(或相加); 否则,先把其中一个方程乘以适当的数,将所得方程与另一个方程相减(或相加),或者先把两个方程分别乘以适当的数,再把所得到的方程相减(或相加). 这种解二元一次方程组的方法叫做加减消元法,简称加减法.用加减消元法解下列方程组:解: ①+② ,得 4y=16解得 y=4把y=4代入①,得
2x+4=-2解得 x=-3因此原方程组的一个解是解: ①-② ,得 -5y=15解得 y=-3把y=-3代入①,得
5x-2×(-3)=11解得 x=1因此原方程组的一个解是解: ①×2,得 6x+4y=16 ③③-②,得 9y=63解得 y=7把y=7代入① ,得
3x+2×7= 8解得 x =-2因此原方程组的一个解是解: ①+② ,得 8x=70解得 把 代入①,得 解得因此原方程组的一个解是解: ①×4,得 12x+16y=44 ③②×3,得 12x-15y=-111 ④③-④ ,得 31y=155解得 y=5把y=5代入① ,得 3x+4×5= 11解得 x =-3因此原方程组的一个解是解: ①×5,得 10x-25y=120 ③②×2,得 10x +4y = 62 ④③-④ ,得 -29y=58解得 y=-2把y=-2代入① ,得
2x-5×(-2)= 24解得 x =7因此原方程组的一个解是例1 方程组 的解是 ( )①+②得
3x = 3, x=1解析B把x=1代入①得
y = 1,所以原方程组的解为故选B. 解方程组解:由①×2+②得:
7x=14,x=2.例2把x=2代入①式得:
y =-2.原方程组的解为 解方程组解:①×3,得
6x+3y=15. ③例3②+③,得
7x =21, x=3,把x=3代入① ,得
2×3+y=5. y=-1.∴原方程组的解为信息时代小窗口:高斯消去法 当今信息时代,由于计算机的迅猛发展,使得实际问题中含有成千上万个未知数的一次方程组有可能求解. 为此需要使消元法有规律可循,让计算机能够机械地执行命令,解一次方程组. 现在我们以下面的二元一次方程组为例,说明这种统一的方法.第一步:把方程组写成如下的标准形式:统一按标准形式把数据输入到计算机中.第二步:把标准形式的方程组化成阶梯形:①× ,加到②上,得 由③、④组成的方程组叫做阶梯形方程组,其中第二个方程(即方程③)已经不含未知数x.第三步:解方程④,得 y=3.往回代入③,解得 x=-1.因此原方程组的一个解是 上述这种解一次方程组的方法叫做高斯消去法,其中第二步叫做消去算法,第三步叫做回代算法. 高斯消去法不仅可以用来解任意一个二元一次方程组,而且可以用来解任意一个三元一次方程组,以及解任意一个n元一次方程组,其中n是任一正整数. (注:有n个未知数,并且含未知数的每一项都是1次的方程叫做n元一次方程. 含有相同未知数的若干个n元一次方程联立起来,组成的方程组叫做n元一次方程组.)高斯消去法可以用下述框图表示:二元一次方程组的标准形式阶梯形方程组出现“0=d”?
其中d是一个数无解或者有
无穷多个解求出唯一解 高斯消去法的实质在我国《九章算术》的“方程”章中就已经具备了.结 束
再代入①,得
这就把x消去了!她得到的y的方程也就是
(3y+17)+5y=9
这不就可以直接从②得,
2x=3y+17,
然后把它代入①吗? 还有没有更简单的解法呢? 方程①和②中都有2x,
为了消去x,干脆把方程①减去方程②就可以了!①-②,得 8y= -8,
解得 y= -1
把y=-1代入①,得
2x+5(-1)=9,
解得 x= 7
因此原方程组的一个解是例3 解方程组:举
例 9x = 9. 解得 x = 1把x=1代入① ,得
7×1+3y = 1因此原方程组的一个解是7x+3y+(2x-3y)=1+8解得 y = -2 两个方程中的未知数y的系数互为相反数,可以消去y. 在上面的两个方程组中,把方程①减去②,或
者把方程①与②相加,便消去了一个未知数,被消
去的未知数的系数有什么特点? 被消去的未知数系数相等或互为相反数. 如何较简便地解下述二元一次方程组? 要是①、②两式中,x的系数相等或者互为相反数就好办了! 把①式两边乘以3,不就行了么!解 ①×3,得 6x+9y=-33 ③ ②-③,得 -14y = 42解得 y= -3把y =-3代入①,得
2x+3×(-3)= -11,解得 x= -1因此原方程组的一个解是例4 解方程组:举
例 能不能使两个方程中x(或y)的系数相等(或互为相反数)呢?解得 y = 5把y=5代入①,得 3x+4×5=8因此原方程组的一个解是将两个方程中的x的系数变为相等.解得 x = -4②×3 ,得
12x+9y=-3. ④③-④ ,得 7y=35. 上面四个方程组中,是如何消去一个未知数的? 消去一个未知数的方法是:如果两个方程中有一个未知数的系数相等(或互为相反数),那么把这两个方程相减(或相加); 否则,先把其中一个方程乘以适当的数,将所得方程与另一个方程相减(或相加),或者先把两个方程分别乘以适当的数,再把所得到的方程相减(或相加). 这种解二元一次方程组的方法叫做加减消元法,简称加减法.用加减消元法解下列方程组:解: ①+② ,得 4y=16解得 y=4把y=4代入①,得
2x+4=-2解得 x=-3因此原方程组的一个解是解: ①-② ,得 -5y=15解得 y=-3把y=-3代入①,得
5x-2×(-3)=11解得 x=1因此原方程组的一个解是解: ①×2,得 6x+4y=16 ③③-②,得 9y=63解得 y=7把y=7代入① ,得
3x+2×7= 8解得 x =-2因此原方程组的一个解是解: ①+② ,得 8x=70解得 把 代入①,得 解得因此原方程组的一个解是解: ①×4,得 12x+16y=44 ③②×3,得 12x-15y=-111 ④③-④ ,得 31y=155解得 y=5把y=5代入① ,得 3x+4×5= 11解得 x =-3因此原方程组的一个解是解: ①×5,得 10x-25y=120 ③②×2,得 10x +4y = 62 ④③-④ ,得 -29y=58解得 y=-2把y=-2代入① ,得
2x-5×(-2)= 24解得 x =7因此原方程组的一个解是例1 方程组 的解是 ( )①+②得
3x = 3, x=1解析B把x=1代入①得
y = 1,所以原方程组的解为故选B. 解方程组解:由①×2+②得:
7x=14,x=2.例2把x=2代入①式得:
y =-2.原方程组的解为 解方程组解:①×3,得
6x+3y=15. ③例3②+③,得
7x =21, x=3,把x=3代入① ,得
2×3+y=5. y=-1.∴原方程组的解为信息时代小窗口:高斯消去法 当今信息时代,由于计算机的迅猛发展,使得实际问题中含有成千上万个未知数的一次方程组有可能求解. 为此需要使消元法有规律可循,让计算机能够机械地执行命令,解一次方程组. 现在我们以下面的二元一次方程组为例,说明这种统一的方法.第一步:把方程组写成如下的标准形式:统一按标准形式把数据输入到计算机中.第二步:把标准形式的方程组化成阶梯形:①× ,加到②上,得 由③、④组成的方程组叫做阶梯形方程组,其中第二个方程(即方程③)已经不含未知数x.第三步:解方程④,得 y=3.往回代入③,解得 x=-1.因此原方程组的一个解是 上述这种解一次方程组的方法叫做高斯消去法,其中第二步叫做消去算法,第三步叫做回代算法. 高斯消去法不仅可以用来解任意一个二元一次方程组,而且可以用来解任意一个三元一次方程组,以及解任意一个n元一次方程组,其中n是任一正整数. (注:有n个未知数,并且含未知数的每一项都是1次的方程叫做n元一次方程. 含有相同未知数的若干个n元一次方程联立起来,组成的方程组叫做n元一次方程组.)高斯消去法可以用下述框图表示:二元一次方程组的标准形式阶梯形方程组出现“0=d”?
其中d是一个数无解或者有
无穷多个解求出唯一解 高斯消去法的实质在我国《九章算术》的“方程”章中就已经具备了.结 束
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
