4.3用乘法公式分解因式(1) 课件(共20张PPT)
文档属性
| 名称 | 4.3用乘法公式分解因式(1) 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 16:42:22 | ||
图片预览







文档简介
(共20张PPT)
4.3用乘法公式因式分解(1)
浙教版 七年级下
复习回顾
下列等式中,哪些是因式分解?哪些不是?为什么?
一个多项式
几个整式的积
有一个必定是多项式
最后一步运算是乘法
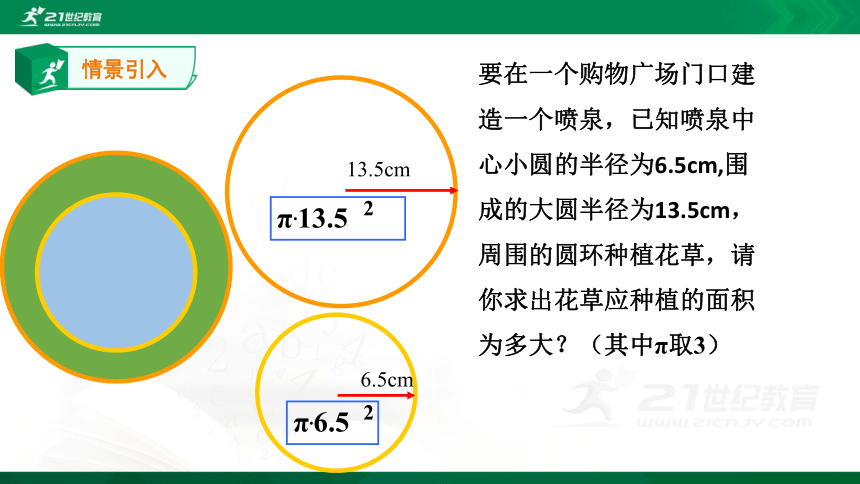
情景引入
13.5cm
6.5cm
π.13.5
2
π.6.5
2
要在一个购物广场门口建造一个喷泉,已知喷泉中心小圆的半径为6.5cm,围成的大圆半径为13.5cm,周围的圆环种植花草,请你求出花草应种植的面积为多大?(其中π取3)
新知探究
π
13.5
2
.
π
.
6.5
2
-
(π取3)
3×13.5 - 3×6.5
2
2
=420!
你能不用计算器快速算出吗?
两者面积之差为(列出算式):
=3×(13.52 - 6.52 )
=3 ×20 ×7
=3 ×(13.5+6.5) (13.5 - 6.5)
新知讲解
把如图卡纸剪开,拼成一张长方形卡纸,作为一幅精美剪纸衬底,怎么剪?你能给出数学解释吗?
a-b
a-b
b
a-b
a2-b2
(a+b)(a-b)
=
两数的平方差等于两数的和与两数差的积。
请用文字叙述一下这个公式?
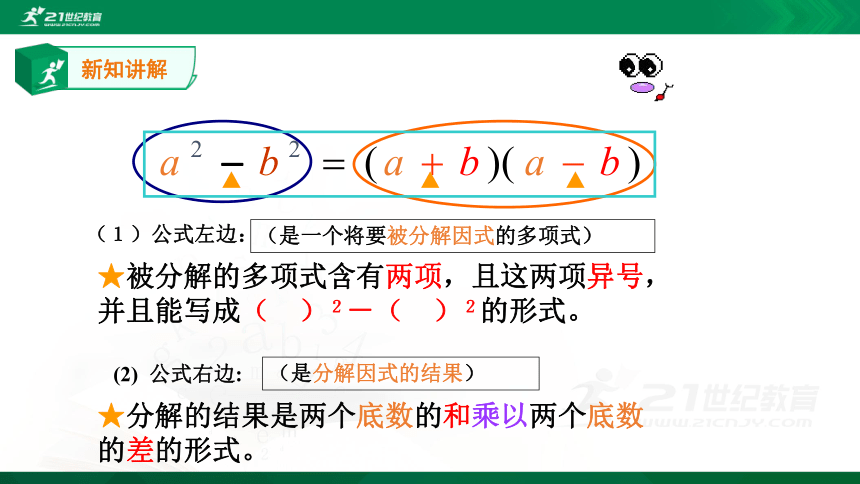
新知讲解
(1)公式左边:
(是一个将要被分解因式的多项式)
★被分解的多项式含有两项,且这两项异号,并且能写成( )2-( )2的形式。
(2) 公式右边:
(是分解因式的结果)
★分解的结果是两个底数的和乘以两个底数的差的形式。
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
▲
▲
▲
巩固练习
(1)4x2+y2 (2) 4x2-(-y)2
(3) -4x2-y2 (4) -4x2+y2
(5) a2-4 (6) a2+3
能
能
能
不能
不能
不能
能用平方差公式分解因式的多项式的特征:
3、每部分都能写成某个式子的平方。
1、由两部分组成; 2、两部分符号相反;
1、下列多项式能否用平方差公式分解因式?说说你的理由。
例题讲解
例1、把下列各式分解因式:
⑴ ⑵
⑶ ⑷
解⑴
⑵
⑶
⑷
小结:一般地,如果一个多项式可以转化为a -b 的形式,那么这个多项式就可以用平方差公式分解因式.
巩固练习
试一试,你能行!
2、下列多项式能转化成( )2-( )2的形式吗?如果能,请将其转化成( )2-( )2的形式。
(1) m2 -1
(2)4m2 -9
(3)4m2+9
(4)x2 -25y 2
(5) -x2 -25y2
(6) -x2+25y2
= m2 -12
= (2m)2 -32
不能转化为平方差形式
= x2 -(5y)2
不能转化为平方差形式
= 25y2-x2 =(5y)2 -x2
a2 - b2= (a + b) (a - b)
巩固练习
3、分解因式:⑴ ⑵
⑶ ⑷
解 ⑴
⑵
⑶
⑷
例题讲解
例2、分解因式:
解:
注意:多项式的因式分解要分解到不能再分解为止.
巩固练习
4、分解因式:
⑴ ⑵
解⑴
⑵
课堂总结
通过本节课的学习,你有哪些收获
分解因式的步骤:
(1)优先考虑提取公因式法
(2)其次看是否能用公式法 (如平方差公式)
(3)务必检查是否分解彻底了
拓展提高
1.把下列各式分解因式:
⑴
⑵
解⑴原式
⑵原式
拓展提高
解:原式=8×(7582-2582)
=8×(758+258)×(758-258)
=8×1 016×500
=4 064 000.
拓展提高
3.若248-1可以被60与70之间的两个整数整除,求这两个数.
解
∴符合条件的因数是65和63.
拓展提高
解:剩余部分的面积为:
a2-4b2=(a+2b)(a-2b)(cm2).
当a=13.2,b=3.4时,(a+2b)(a-2b)=(13.2+2×3.4) ×(13.2-2×3.4)=20×6.4=128,
即剩余部分的面积为128 cm2.
拓展提高
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
4.3用乘法公式因式分解(1)
浙教版 七年级下
复习回顾
下列等式中,哪些是因式分解?哪些不是?为什么?
一个多项式
几个整式的积
有一个必定是多项式
最后一步运算是乘法
情景引入
13.5cm
6.5cm
π.13.5
2
π.6.5
2
要在一个购物广场门口建造一个喷泉,已知喷泉中心小圆的半径为6.5cm,围成的大圆半径为13.5cm,周围的圆环种植花草,请你求出花草应种植的面积为多大?(其中π取3)
新知探究
π
13.5
2
.
π
.
6.5
2
-
(π取3)
3×13.5 - 3×6.5
2
2
=420!
你能不用计算器快速算出吗?
两者面积之差为(列出算式):
=3×(13.52 - 6.52 )
=3 ×20 ×7
=3 ×(13.5+6.5) (13.5 - 6.5)
新知讲解
把如图卡纸剪开,拼成一张长方形卡纸,作为一幅精美剪纸衬底,怎么剪?你能给出数学解释吗?
a-b
a-b
b
a-b
a2-b2
(a+b)(a-b)
=
两数的平方差等于两数的和与两数差的积。
请用文字叙述一下这个公式?
新知讲解
(1)公式左边:
(是一个将要被分解因式的多项式)
★被分解的多项式含有两项,且这两项异号,并且能写成( )2-( )2的形式。
(2) 公式右边:
(是分解因式的结果)
★分解的结果是两个底数的和乘以两个底数的差的形式。
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
▲
▲
▲
巩固练习
(1)4x2+y2 (2) 4x2-(-y)2
(3) -4x2-y2 (4) -4x2+y2
(5) a2-4 (6) a2+3
能
能
能
不能
不能
不能
能用平方差公式分解因式的多项式的特征:
3、每部分都能写成某个式子的平方。
1、由两部分组成; 2、两部分符号相反;
1、下列多项式能否用平方差公式分解因式?说说你的理由。
例题讲解
例1、把下列各式分解因式:
⑴ ⑵
⑶ ⑷
解⑴
⑵
⑶
⑷
小结:一般地,如果一个多项式可以转化为a -b 的形式,那么这个多项式就可以用平方差公式分解因式.
巩固练习
试一试,你能行!
2、下列多项式能转化成( )2-( )2的形式吗?如果能,请将其转化成( )2-( )2的形式。
(1) m2 -1
(2)4m2 -9
(3)4m2+9
(4)x2 -25y 2
(5) -x2 -25y2
(6) -x2+25y2
= m2 -12
= (2m)2 -32
不能转化为平方差形式
= x2 -(5y)2
不能转化为平方差形式
= 25y2-x2 =(5y)2 -x2
a2 - b2= (a + b) (a - b)
巩固练习
3、分解因式:⑴ ⑵
⑶ ⑷
解 ⑴
⑵
⑶
⑷
例题讲解
例2、分解因式:
解:
注意:多项式的因式分解要分解到不能再分解为止.
巩固练习
4、分解因式:
⑴ ⑵
解⑴
⑵
课堂总结
通过本节课的学习,你有哪些收获
分解因式的步骤:
(1)优先考虑提取公因式法
(2)其次看是否能用公式法 (如平方差公式)
(3)务必检查是否分解彻底了
拓展提高
1.把下列各式分解因式:
⑴
⑵
解⑴原式
⑵原式
拓展提高
解:原式=8×(7582-2582)
=8×(758+258)×(758-258)
=8×1 016×500
=4 064 000.
拓展提高
3.若248-1可以被60与70之间的两个整数整除,求这两个数.
解
∴符合条件的因数是65和63.
拓展提高
解:剩余部分的面积为:
a2-4b2=(a+2b)(a-2b)(cm2).
当a=13.2,b=3.4时,(a+2b)(a-2b)=(13.2+2×3.4) ×(13.2-2×3.4)=20×6.4=128,
即剩余部分的面积为128 cm2.
拓展提高
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
