4.3用乘法公式因式分解(2) 课件(共22张PPT)
文档属性
| 名称 | 4.3用乘法公式因式分解(2) 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 16:52:02 | ||
图片预览








文档简介
(共22张PPT)
4.3用公式法因式分解(2)
浙教版 七年级下
复习回顾
上节课后老师布置了作业,要求把下列各式分解因式。
某位同学的答案如下,请帮助老师批改一下。
?
一“提”
二“选”
三“检验”
平方差公式
提公因式
新知探究
现在我们把完全平方公式反过来,可得:
两数的平方和,加上 这两数的积的2倍,等于这两数和 的平方.
完全平方公式:
(或者减去)
(或者差)
新知探究
两数的平方和,加上(或者减去)这两数的积的2倍,等于这两数和(或者差)的平方.
形如 的多项式称为完全平方式.
新知讲解
两数的平方和,加上(或者减去)这两数的积的2倍,等于这两个数和(或者差)的平方.
用完全平方公式分解因式的关键是:判断这个多项式是不是一个完全平方式.
形如 及 的多项式,叫做完全平方式.
巩固练习
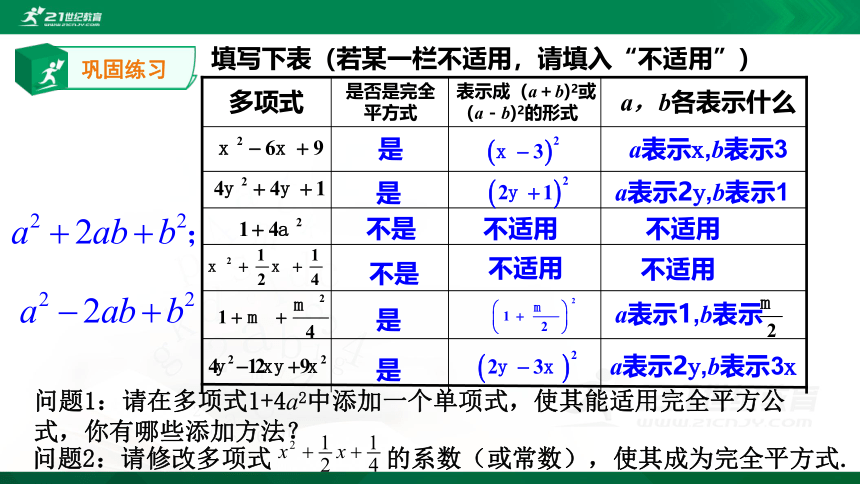
问题1:请在多项式1+4a2中添加一个单项式,使其能适用完全平方公式,你有哪些添加方法?
问题2:请修改多项式 的系数(或常数),使其成为完全平方式.
填写下表(若某一栏不适用,请填入“不适用”)
a表示x,b表示3
a,b各表示什么
表示成(a+b)2或(a-b)2的形式
是
是否是完全平方式
多项式
是
a表示2y,b表示1
不是
不适用
不适用
不适用
不适用
不是
是
是
a表示2y,b表示3x
a表示1,b表示
新知归纳
完全平方式特征:
(1)多项式有3项;
(2)两项平方项,且符号都为正,另一项为中间项(这两数积的2倍).
先确定平方项,再检查剩余项是否符合两数积的2倍(中间项).
判断方法:
是不是完全平方式?
巩固练习
请补上一项,使下列多项式成为完全平方式.
例题讲解
例1、把下列各式分解因式:⑴
⑵ ⑶
解⑴
⑵
⑶
一“提”
二“选”
三“检验”
首项为负,一般需提出负号
有公因式要先提公因式
例题讲解
例2、分解因式:
分析 把(2x+y)看做一个整体,多项式就是一个关于(2x+y)的完全平方式.
解
注意:此例的解法是灵活地把2x+y看做一个整体,这种数学思想称为换元思想.
试一试:
巩固练习
1.分解因式:⑴ ⑵
⑶ ⑷
⑸
巩固练习
2.下面的因式分解对吗?为什么?
⑴ ⑵
⑶
⑷
⑴错.左边不是完全平方式.
⑵错.左边不是完全平方式.
⑶错.左边不是完全平方式.
⑷错.提取-1后不是两数差的完全平方式,而是两数和完全平方式.
当堂小结
(1)形如________________形式的多项式可以用完全平方公式分解因式。
(3)因式分解要_________。
(2)因式分解通常先考虑______________方法。
本节课你学会了什么?
提取公因式法
彻底
你还体验到了哪些数学思想?
类比思想
整体(换元)思想
拓展提高
B
拓展提高
±7
4x4(答案不唯一)
解:原式=(39.8-49.8)2=(-10)2=100.
拓展提高
解:原式=(a2-4+3)2=(a2-1)2=(a+1)2(a-1)2.
解:原式=(x2+16y2)2-(8xy)2
=(x2+16y2+8xy)(x2+16y2-8xy)
=(x+4y)2(x-4y)2.
拓展提高
解:原式=a(a2-1)+2b(1-a2)=(a-2b)(a+1)(a-1).
解:原式=(x-y)2+2(x-y)+1=(x-y+1)2.
拓展提高
拓展提高
解:[(x-y)2+4xy][(x+y)2-4xy]
=(x2+2xy+y2)(x2-2xy+y2)
=(x+y)2(x-y)2
=[(x+y)(x-y)]2
=(x2-y2)2
=400.
拓展提高
探究活动
9.观察下表,你还能继续往下写吗?
…
…
7
5
3
1
你发现了什么规律?能用因式分解来说明你发现的规律吗?
任何一个正奇数都可以表示成两个相邻自然数的平方差。对于正奇数2n+1(n为自然数),有
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
4.3用公式法因式分解(2)
浙教版 七年级下
复习回顾
上节课后老师布置了作业,要求把下列各式分解因式。
某位同学的答案如下,请帮助老师批改一下。
?
一“提”
二“选”
三“检验”
平方差公式
提公因式
新知探究
现在我们把完全平方公式反过来,可得:
两数的平方和,加上 这两数的积的2倍,等于这两数和 的平方.
完全平方公式:
(或者减去)
(或者差)
新知探究
两数的平方和,加上(或者减去)这两数的积的2倍,等于这两数和(或者差)的平方.
形如 的多项式称为完全平方式.
新知讲解
两数的平方和,加上(或者减去)这两数的积的2倍,等于这两个数和(或者差)的平方.
用完全平方公式分解因式的关键是:判断这个多项式是不是一个完全平方式.
形如 及 的多项式,叫做完全平方式.
巩固练习
问题1:请在多项式1+4a2中添加一个单项式,使其能适用完全平方公式,你有哪些添加方法?
问题2:请修改多项式 的系数(或常数),使其成为完全平方式.
填写下表(若某一栏不适用,请填入“不适用”)
a表示x,b表示3
a,b各表示什么
表示成(a+b)2或(a-b)2的形式
是
是否是完全平方式
多项式
是
a表示2y,b表示1
不是
不适用
不适用
不适用
不适用
不是
是
是
a表示2y,b表示3x
a表示1,b表示
新知归纳
完全平方式特征:
(1)多项式有3项;
(2)两项平方项,且符号都为正,另一项为中间项(这两数积的2倍).
先确定平方项,再检查剩余项是否符合两数积的2倍(中间项).
判断方法:
是不是完全平方式?
巩固练习
请补上一项,使下列多项式成为完全平方式.
例题讲解
例1、把下列各式分解因式:⑴
⑵ ⑶
解⑴
⑵
⑶
一“提”
二“选”
三“检验”
首项为负,一般需提出负号
有公因式要先提公因式
例题讲解
例2、分解因式:
分析 把(2x+y)看做一个整体,多项式就是一个关于(2x+y)的完全平方式.
解
注意:此例的解法是灵活地把2x+y看做一个整体,这种数学思想称为换元思想.
试一试:
巩固练习
1.分解因式:⑴ ⑵
⑶ ⑷
⑸
巩固练习
2.下面的因式分解对吗?为什么?
⑴ ⑵
⑶
⑷
⑴错.左边不是完全平方式.
⑵错.左边不是完全平方式.
⑶错.左边不是完全平方式.
⑷错.提取-1后不是两数差的完全平方式,而是两数和完全平方式.
当堂小结
(1)形如________________形式的多项式可以用完全平方公式分解因式。
(3)因式分解要_________。
(2)因式分解通常先考虑______________方法。
本节课你学会了什么?
提取公因式法
彻底
你还体验到了哪些数学思想?
类比思想
整体(换元)思想
拓展提高
B
拓展提高
±7
4x4(答案不唯一)
解:原式=(39.8-49.8)2=(-10)2=100.
拓展提高
解:原式=(a2-4+3)2=(a2-1)2=(a+1)2(a-1)2.
解:原式=(x2+16y2)2-(8xy)2
=(x2+16y2+8xy)(x2+16y2-8xy)
=(x+4y)2(x-4y)2.
拓展提高
解:原式=a(a2-1)+2b(1-a2)=(a-2b)(a+1)(a-1).
解:原式=(x-y)2+2(x-y)+1=(x-y+1)2.
拓展提高
拓展提高
解:[(x-y)2+4xy][(x+y)2-4xy]
=(x2+2xy+y2)(x2-2xy+y2)
=(x+y)2(x-y)2
=[(x+y)(x-y)]2
=(x2-y2)2
=400.
拓展提高
探究活动
9.观察下表,你还能继续往下写吗?
…
…
7
5
3
1
你发现了什么规律?能用因式分解来说明你发现的规律吗?
任何一个正奇数都可以表示成两个相邻自然数的平方差。对于正奇数2n+1(n为自然数),有
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
