第二章二元一次方程组同步训练

课件17张PPT。第二章二元一次方程组同步训练二元一次方程组知识网络图定 义二元一次方程组的解基本解法基本思路应用－列方程组解应用题代入法加减法消元解题思路：消元（即减少未知数）
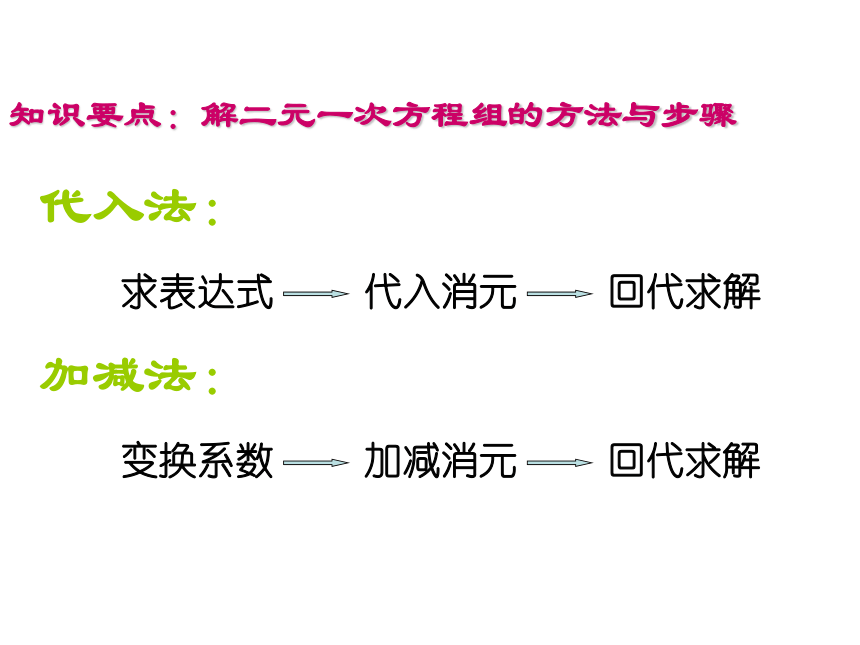
一、知识梳理： 1、什么样的方程是二元一次方程？定义：含有两个未知数，并且所含的未知数的项的次数都是1的方程，叫做二元一次方程.练习：1、请判断下列各方程中，哪些是二元一次方程，哪些不是？并说明理由.(1)2x+5y=10(2) 2x+y+z=1(5)2a+3b=5(6)2x+10 =0下面4组数值中，哪些是二元一次方程2x+y=10的解？知识要点：3、什么是二元一次方程组？知识要点：2、什么叫做二元一次方程的解？小结：适合一个二元一次方程的一组未知数的值，叫做二元一次方程的解.含有两个未知数的两个一次方程组成的一组方程，叫做二元一次方程组. 解二元一次方程组的基本思想是什么？知识要点：解二元一次方程组的方法与步骤代入法：求表达式代入消元回代求解加减法：变换系数加减消元回代求解1、当方程组中的方程中有未知数的系数是_____或______，
或者有方程的常数项为______时，选用代入法消元。2、当方程组中有未知数的系数的___________相等，或
成倍数时，选用加减法消元。3、一般先把方程组整理成____________形式后，再选择
加减消元。－1零绝对值请同学们归纳一下：
什么样的方程组用“代入法”？
什么样的方程组用“加减法”？练习：
1、已知3x+4y=12，用含有x的未知数表示y,则
2、写出3x+y=12的所有正整数解 .
y=3-0.75x选择系数不是1的项作为尝试对象，可提升速度，如本题，选X较方便。变式；写出x+6y=28的所有自然数解 方程组的应用3x2a-b+5y3a+b-8=8是关于x、y的二元一次方程求a、b得：a=b=23思路归类：利用“ 次数为1”来解题。非一次项的系数必须为0一次项的指数必须为1得：a=b=23 方程组的应用 分析：由于一个数的平方是一个非负数，一个数的绝对值也是一个非负数；两个非负数的和为零就只能是每个数都为零，因此，原方程就转化为方程组：已知 ，求 、 的值． 重点：如果已知几个非负数的和为零，则这几个数均为零。 方程组的应用　m , n 为何值时， 是同类项。解题思路：相同字母的指数相同。 方程组的应用例、已知 是方程组 的解,则 -10 方程组的应用重组方程组0.5x单位x单位0.7y单位0.4y单位设每餐需要甲、乙两种原料各x,y克，则有下表由上表可以得到的等式：0.5x+0.7y=35x+0.4y=40 通过解二元一次方程组即可获得所需的答案(0.5x+0.7y)单位(x+0.4y)单位例、医院用甲、乙两种原料为手术后的病人配制营养品.每克甲原料含0.5单位蛋白质1单位铁质，每克乙原料含0.7单位蛋白质和0.4单位铁质.若病人每餐需要35单位蛋白质40单位铁质，那么每餐甲、乙两种原料各多少克恰好满足病人的需要？｛思路点拔：利用表格来理清数量关系是一种常用的分析方法。例、某体育场的环行跑道长400米，甲、乙分别以一定的速度练习长跑和自行车，如果反向而行，那么他们每隔30秒相遇一次，如果同向而行，那么每隔80秒乙追上甲一次，求甲乙的速度.解：设甲的速度是每秒x米，乙的速度是每秒y米.依题意得：相向而行：路程和同向而行（追及问题）：路程差 方程组的应用船在顺水中的速度为48km/h，在逆水中的速度为24km/h, 则船在静水中的速度为多少？思路点拨：顺水速度=静水中的船的速度+水速
逆水速度=静水中的船的速度-水速解：设船在静水中的速度为xkm/h，水速为ykm/h。再见