3.1同底数幂的乘法(2)
图片预览










文档简介
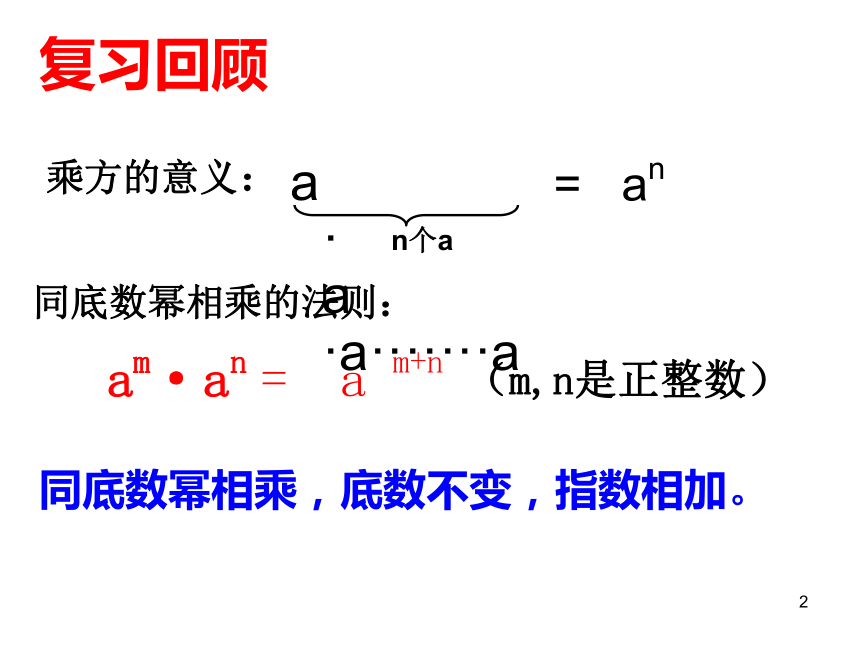
课件36张PPT。13.1 同底数幂的乘法(2)瑞安市东山中学幂的乘方2复习回顾a·a·a·······an个a= an同底数幂相乘的法则:am·an = a m+n(m,n是正整数)乘方的意义:同底数幂相乘,底数不变,指数相加。3计算下列各题:4 如果这个正方体的棱长是 42 cm,那么它的体积是 cm3. 你知道 (42)3 是多少个 4 相乘吗?你知道吗?(42)35做一做合作学习:根据乘方的意义和同底数幂的乘法法则填空:6计算下列各式,并说明理由
(1)(102)3 (2)(34)2
(3)(a3)5 (4)(am)n解(1)(102)3=102×102×102(根据幂的意义)
=102+2+2(根据同底幂相乘法则)
=102×3
(2)(34)2=34×34=34+4=34×2=38
(3)(a3)5=a3·a3·a3·a3·a3=a3+3+3+3+3
=a3×5=a15试一试7 ( am )n= am×am×…×am=am+m+···+mn个an个m= am n底数(不变)(相乘)—— 乘方的意义——同底数幂相乘(其中m , n都是正整数)试猜想探索:m×8幂的乘方法则:这就是说,(am)n与(an)m相等吗?为什么?请思考:9解:= 10 7×3= 10212) (a4)83)(-53)34)[(-3)6]3= a 4×8= a 32= - 5 3×3=-5 9= (36)3=3 181)(107)35) - (y4)3 =- y4×3 =-y126)[(a-b)3 ]2=(a-b)3 ×2 =(a-b)6例1、计算:
1) (107)3 2) (a4)8
3) (-5 3)3 4) [(-3)6]3
5) -(y4)3 6) [(a-b)3]2例题讲解10⑴ (a2)4⑵(b3m)4⑶ (xn)m⑷ (b3)3⑸ x4·x4⑹ (x4)7
⑻ (a3)3⑽ (x6)5⑺ -(y7)2⑾ [(x+y)3]4⑼ [(-1)3]5 ⑿ [(a+1)3]n口答:11抢答:⑵ (x3)4 (x )⑶ - (x5)2⑴ x4·x3⑷ [(x+y)3]4=x7=(x+y)12=x × x10=x
=-x1025122212 辨一辨:下面的计算对吗?如果不对 ,应怎样改正?
(43) 5 = 4 8
(-23)8= (-2)24
[(-3) 5 ] 3 = -315
(52 )4 ×5 = 58
(×) 415(×) 224(√) (×) 5913练习:(口答)
1) (a3)4
2) a3·a4
3) ( y4)2
4) y4 · y 2
5) ( b m )2
6) b m · b 2= a= b2m= b2+m= a12= y8= y6幂的乘方同底数幂相乘想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?714幂的乘方法则:其中m , n都是正整数同底数幂的乘法法则:15底数不变指数相乘指数相加其中m , n都是正整数16练一练:1.填空:(用幂的形式表示结果)
(a3)4= ; a3.a4 = ;
(bm)2= ; x3+x3= ;
-(-y2)4= ; (x2n)2n= .2.计算下列各式,结果用幂的形式表示:
(73)4 (2)[(-10)3]5 (3)(a2)3.a4
(4) (b3)2+(b2)3 (5)-(-y2)5 (6)[(x+1)3]4a12a7b2m2x3-y817例2、计算:解:(1)原式=(2)原式=18练一练:说出下面每一步计算理由,并将它们填入括号内:
(p2)3.(p5)2
=p6.p10 ( )
=p6+10 ( )
=p16幂的乘方法则同底数幂的乘法法则19例3:幂的乘方的逆运算:
(1).1010 = ( )2 = ( )5
(2) x13·x7 =x( ) =( )5 =( )4 =( )10
(3)a2m =( )2 =( )m (m为正整数)
105
10220x4x5x2ama220(3):若10a=2,10b=3, 则10a+b=____,
102a+103b=_____,102a+3b=_____
(1):an=3,则a3n=___.(2):am=3,an=4,则am+n=____,a2m+3n=____.271257663110821
⑴ 85=2( )⑵ a12=(a3)( )
=(a2)( )
= a3 ·a( )注:幂运算性质均可逆向应用am·an=am+n(am) n=am n15469填一填:22例题4.胡华现在想做一个棱长为40cm的立方体,但她身边只有1
平方米的硬纸,请问她能否做成?231、计算:
⑴ (a2)3 ⑵ a2·a3
⑶ (y5)5 ⑷ y5·y52、计算:
⑴ (x2)3· (x2)2 ⑵ (y3)4· (y4)3
⑶ -(xn)2· (x3)2m ⑷ (a2)3+a3 · a324例题5.观察下列各式;通过观察,用你所发现的规律写出 的末位数字是( )A.2 B.4 C.8 D.6解:的末位数字相同,即为4.B25练习:一个正方体的物体的棱长为 厘米,则它的体积是多少?若每立方厘米的重量为 克,则这个正方体的重量为多少
千克?解:答:这个正方体的重量为 千克。26课堂小结幂的乘方运算法则
(am)n=amn(m,n都是正整数)
底数不变,指数相乘同底数幂相乘法则:
am·an=am+n(m,n都是正整数)
底数不变,指数相加27§3.1同底数幂的乘法(2)幂的乘方法则
1.法则:幂的乘方,底数不变,指数相乘。2.应用法则时的注意事项:(1)幂的乘方法则是根据乘方的定义,同
底数的幂相乘得到的,此性质可以逆用,即;
解题时要灵活应用;
(2)幂的乘方与同底数幂的乘法不能相互混淆,相同点是:底数不变;不同点
是:幂的乘方的指数是相乘的;而同底数幂的乘法的指数是相加的。
(3)在进行幂的运算时,如果遇到几个底数为负数的幂相乘时,应先确定整个积的
符号然后再运算;
(4)幂的乘方法则中的底数a可以是任意有理数,也可以是单项式或多项式;
(5)在进行幂的乘法和幂的乘方混合运算时,要注意运算顺序,即,先乘方后相乘.
(6)幂的乘方法则可以推广;即28【1】、复习、整理、巩固今天所学知识。一、必做题:1、作业本(2)第14--15页T1—T7;
2、参书第64页A组题T1—T4;
3.课时特训第35、36页T1—T17
二、选做题:1、参书第64页B组题T5、T6;
2.拓展探究题:参看幻灯片第29--34号。
三、抄写第25张幻灯片的内容。【2】、书面作业布置作业:29拓展练习:1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.8672303、在255,344,433,522,这四个幂的数值中,最大的一个是_______ 3444、已知 =a,试用a的代数式表示5、已知 ,求 的值31(1).若
(2)若
(3).若2x+5y-3=0,则4x.32y= ____(4).若x是3的立方根,求x6的值 6.做一做32(6)、若 am = 2, 则a3m =_____.
(7)、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.867233(8)比较 355,444,533 的大小。解: ∵ 355 =(35)11 = 24311
444 =(44)11 = 25611
533 =(53)11 = 12511
∴ 444 >355 > 5333435再见祝同学们 学习进步!36DFEGH
(1)(102)3 (2)(34)2
(3)(a3)5 (4)(am)n解(1)(102)3=102×102×102(根据幂的意义)
=102+2+2(根据同底幂相乘法则)
=102×3
(2)(34)2=34×34=34+4=34×2=38
(3)(a3)5=a3·a3·a3·a3·a3=a3+3+3+3+3
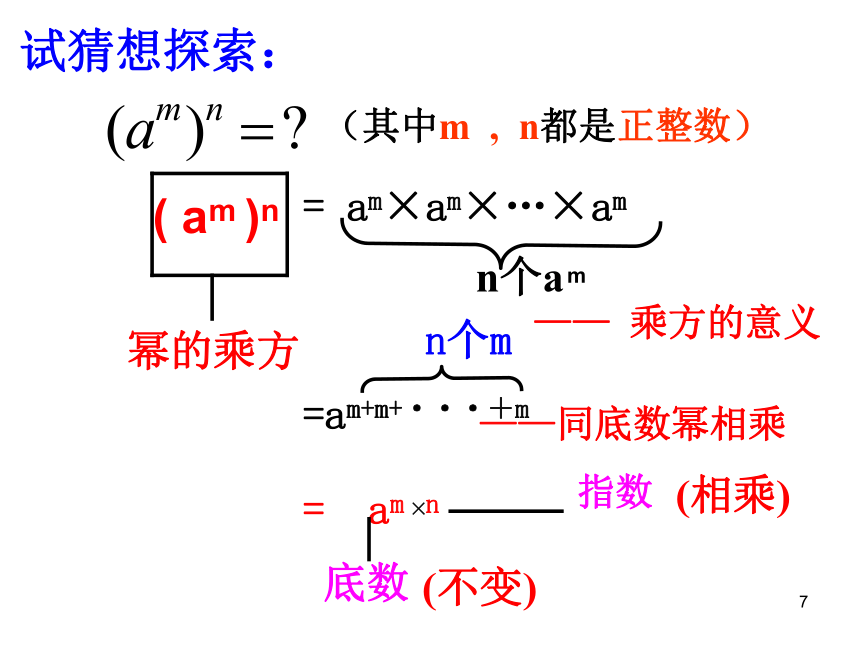
=a3×5=a15试一试7 ( am )n= am×am×…×am=am+m+···+mn个an个m= am n底数(不变)(相乘)—— 乘方的意义——同底数幂相乘(其中m , n都是正整数)试猜想探索:m×8幂的乘方法则:这就是说,(am)n与(an)m相等吗?为什么?请思考:9解:= 10 7×3= 10212) (a4)83)(-53)34)[(-3)6]3= a 4×8= a 32= - 5 3×3=-5 9= (36)3=3 181)(107)35) - (y4)3 =- y4×3 =-y126)[(a-b)3 ]2=(a-b)3 ×2 =(a-b)6例1、计算:
1) (107)3 2) (a4)8
3) (-5 3)3 4) [(-3)6]3
5) -(y4)3 6) [(a-b)3]2例题讲解10⑴ (a2)4⑵(b3m)4⑶ (xn)m⑷ (b3)3⑸ x4·x4⑹ (x4)7
⑻ (a3)3⑽ (x6)5⑺ -(y7)2⑾ [(x+y)3]4⑼ [(-1)3]5 ⑿ [(a+1)3]n口答:11抢答:⑵ (x3)4 (x )⑶ - (x5)2⑴ x4·x3⑷ [(x+y)3]4=x7=(x+y)12=x × x10=x
=-x1025122212 辨一辨:下面的计算对吗?如果不对 ,应怎样改正?
(43) 5 = 4 8
(-23)8= (-2)24
[(-3) 5 ] 3 = -315
(52 )4 ×5 = 58
(×) 415(×) 224(√) (×) 5913练习:(口答)
1) (a3)4
2) a3·a4
3) ( y4)2
4) y4 · y 2
5) ( b m )2
6) b m · b 2= a= b2m= b2+m= a12= y8= y6幂的乘方同底数幂相乘想一想:同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点?714幂的乘方法则:其中m , n都是正整数同底数幂的乘法法则:15底数不变指数相乘指数相加其中m , n都是正整数16练一练:1.填空:(用幂的形式表示结果)
(a3)4= ; a3.a4 = ;
(bm)2= ; x3+x3= ;
-(-y2)4= ; (x2n)2n= .2.计算下列各式,结果用幂的形式表示:
(73)4 (2)[(-10)3]5 (3)(a2)3.a4
(4) (b3)2+(b2)3 (5)-(-y2)5 (6)[(x+1)3]4a12a7b2m2x3-y817例2、计算:解:(1)原式=(2)原式=18练一练:说出下面每一步计算理由,并将它们填入括号内:
(p2)3.(p5)2
=p6.p10 ( )
=p6+10 ( )
=p16幂的乘方法则同底数幂的乘法法则19例3:幂的乘方的逆运算:
(1).1010 = ( )2 = ( )5
(2) x13·x7 =x( ) =( )5 =( )4 =( )10
(3)a2m =( )2 =( )m (m为正整数)
105
10220x4x5x2ama220(3):若10a=2,10b=3, 则10a+b=____,
102a+103b=_____,102a+3b=_____
(1):an=3,则a3n=___.(2):am=3,an=4,则am+n=____,a2m+3n=____.271257663110821
⑴ 85=2( )⑵ a12=(a3)( )
=(a2)( )
= a3 ·a( )注:幂运算性质均可逆向应用am·an=am+n(am) n=am n15469填一填:22例题4.胡华现在想做一个棱长为40cm的立方体,但她身边只有1
平方米的硬纸,请问她能否做成?231、计算:
⑴ (a2)3 ⑵ a2·a3
⑶ (y5)5 ⑷ y5·y52、计算:
⑴ (x2)3· (x2)2 ⑵ (y3)4· (y4)3
⑶ -(xn)2· (x3)2m ⑷ (a2)3+a3 · a324例题5.观察下列各式;通过观察,用你所发现的规律写出 的末位数字是( )A.2 B.4 C.8 D.6解:的末位数字相同,即为4.B25练习:一个正方体的物体的棱长为 厘米,则它的体积是多少?若每立方厘米的重量为 克,则这个正方体的重量为多少
千克?解:答:这个正方体的重量为 千克。26课堂小结幂的乘方运算法则
(am)n=amn(m,n都是正整数)
底数不变,指数相乘同底数幂相乘法则:
am·an=am+n(m,n都是正整数)
底数不变,指数相加27§3.1同底数幂的乘法(2)幂的乘方法则
1.法则:幂的乘方,底数不变,指数相乘。2.应用法则时的注意事项:(1)幂的乘方法则是根据乘方的定义,同
底数的幂相乘得到的,此性质可以逆用,即;
解题时要灵活应用;
(2)幂的乘方与同底数幂的乘法不能相互混淆,相同点是:底数不变;不同点
是:幂的乘方的指数是相乘的;而同底数幂的乘法的指数是相加的。
(3)在进行幂的运算时,如果遇到几个底数为负数的幂相乘时,应先确定整个积的
符号然后再运算;
(4)幂的乘方法则中的底数a可以是任意有理数,也可以是单项式或多项式;
(5)在进行幂的乘法和幂的乘方混合运算时,要注意运算顺序,即,先乘方后相乘.
(6)幂的乘方法则可以推广;即28【1】、复习、整理、巩固今天所学知识。一、必做题:1、作业本(2)第14--15页T1—T7;
2、参书第64页A组题T1—T4;
3.课时特训第35、36页T1—T17
二、选做题:1、参书第64页B组题T5、T6;
2.拓展探究题:参看幻灯片第29--34号。
三、抄写第25张幻灯片的内容。【2】、书面作业布置作业:29拓展练习:1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.8672303、在255,344,433,522,这四个幂的数值中,最大的一个是_______ 3444、已知 =a,试用a的代数式表示5、已知 ,求 的值31(1).若
(2)若
(3).若2x+5y-3=0,则4x.32y= ____(4).若x是3的立方根,求x6的值 6.做一做32(6)、若 am = 2, 则a3m =_____.
(7)、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.867233(8)比较 355,444,533 的大小。解: ∵ 355 =(35)11 = 24311
444 =(44)11 = 25611
533 =(53)11 = 12511
∴ 444 >355 > 5333435再见祝同学们 学习进步!36DFEGH
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
