3.1同底数幂的乘法
图片预览







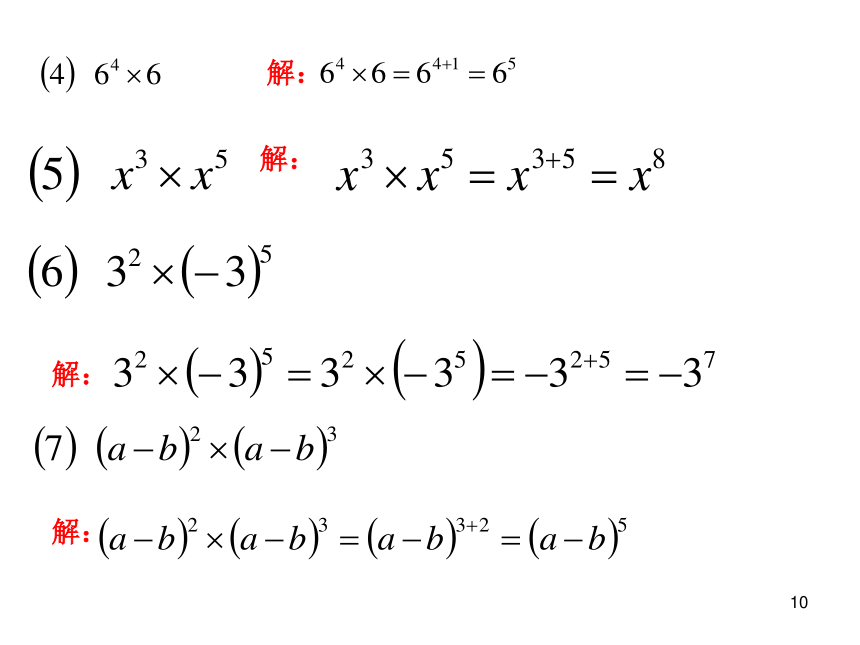


文档简介
课件32张PPT。光年是长度的单位,1光
年是指光经过一年所行
的距离,光的速度是
3.0×105千米/秒,若
一年以365天计,
则1光年大约是多少千米?3.0×105×3.65×102=(3.0×3.65)×(105×102)1瑞安市东山中学§3.1同底数幂的乘法(1)1 an 表示的意义是什么?其中a、n、an分 别叫做什么? an底数幂指数an = a × a × a ×… a
n个a
1问题(1) 23、22表示什么?
23 = ----------------.
22 = ----------------------------- 2×2×2(乘方的意义)回顾 探究2×2问题(2) 23 ×22表示什么? 2×2×2 2×22×2×2×2×2问题(3) 23 ×22该怎么算? 51探索 发现
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
= 5 × 5 × 5 × 5 × 5 × 5 × 5
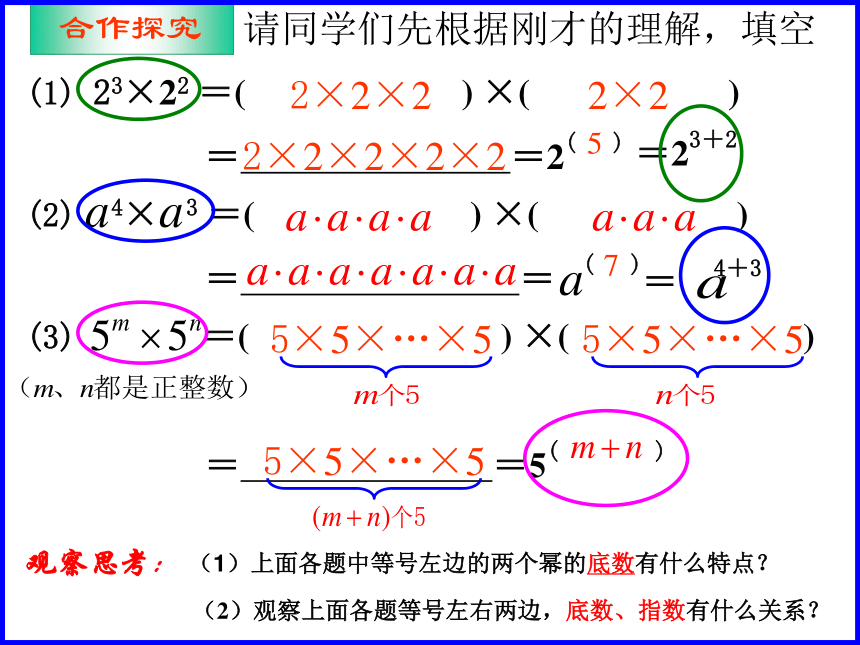
=5723 ×2453×54=(2 ×2 ×2) ×(2 ×2 ×2 ×2)= 2 ×2 ×2 ×2 × 2 ×2 ×2(乘方的意义)(乘法结合律)(乘方的意义)(乘方的意义)(乘方的意义)(乘法结合律)1观察思考: (1)上面各题中等号左边的两个幂的底数有什么特点?
(2)观察上面各题等号左右两边,底数、指数有什么关系?
(1) 23×22 =( ) ×( )
= =2( )(2) 4× 3 =( ) ×( )
= = ( )(3) =( ) ×( )
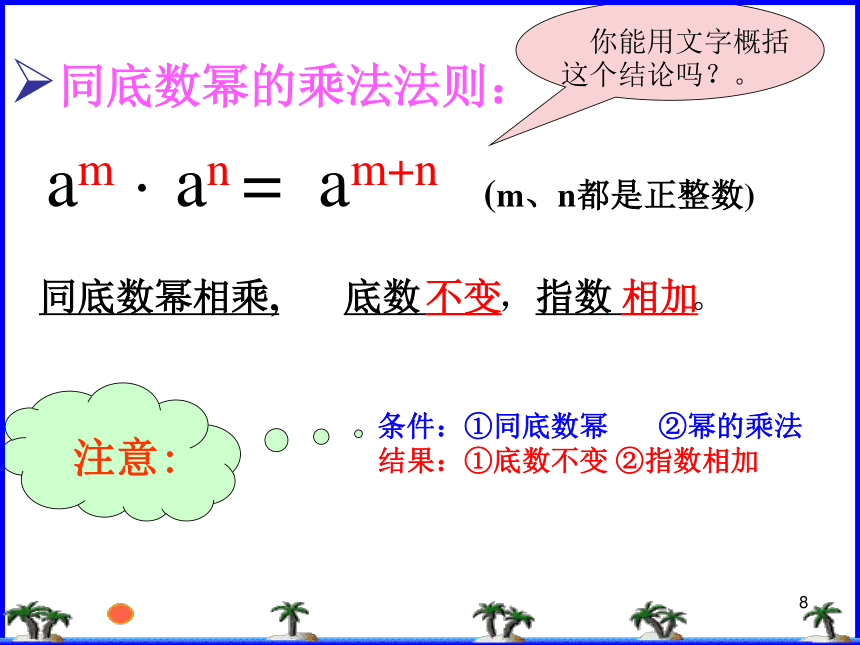
= =5( )=23+22×2×22×22×2×2×2×2575×5×…×55×5×…×55×5×…×5请同学们先根据刚才的理解,填空1猜想: am · an= (m、n都是正整数) am · an =m个an个a= aa…a=am+n(m+n)个a(aa…a)(aa…a)am+n(乘方的意义)(乘法结合律)(乘方的意义)1am · an = am+n (m、n都是正整数)同底数幂相乘,底数 ,指数 。不变相加 同底数幂的乘法法则:条件:①同底数幂 ②幂的乘法
结果:①底数不变 ②指数相加1例1、计算下列各式,结果用幂的形式表示:
(1)78×73
(2)(-2)8×(-2)7
(3) a· a3 am · an = am+n
解:原式=78+3=711解:原式=(-2)8+7=(-2)15解:原式=a1+3=a4=-215同底数幂的乘法公式11 1.同底数幂 ,底数 ,指数 .不变相加相乘
2.???口答(A组): (2) a7 ×a(1) 105×105第一关( 4 )3×33( 5) x 3n+1 · x 2n-1( 6 ) a + a + a(3)(-3)2×(-3)31 b5 · b5= b10 b5 + b5 = 2b5 x2 · x3 = x5 a · a6 = a7× × ××(3)x2 ·x3 = x6 ( ) (5)a · a6 = a6 ( )下面的计算对不对?如果不对,怎样改正?(1)b5 + b5 = b10 ( ) (2)b5 · b5= 2b5( ) (4)73×78= 711( )√1(2) (-2)5×23(1) -28×27例2:注意观察下列各式,然后计算,结果用幂的形式表示:公式: am · an = am+n 解:原式= -( 28×27)=-215解:原式= - 25×23 =-(25×23 )=-28(3) (a-b)2×(a-b)解:原式= (a-b)2+1= (a-b)3若底数不同,先化为相同,后运用法则.
公式中的a可为一个有理数、单项式或多项式(整体思想)
1
2.???计算(B组): 解:原式=c5 × c6=c11 解:原式 =-b6 (3) c5 × (-c)6 (2) -b5 ×b 若底数不相同,应先化相同第二关 (1) 74 × (-7)3 解:原式= - 74 × 73
= - 77
1am · an · ap 等于什么?根据上面的知识进行计算:
b· b3· b5解: b· b3· b5
= b1+3+5
= b9
1例3我国“天河-1A”超级计算机的实测运算速度达到每秒2.566千万亿次。如果按这个速度工作一整天,那么它能运算多少次?解 2.566千万亿次= 24时=由乘法的交换律和结合律,得
(2.566×107×108)× (24×3.6×103)答:它一天约能运算2.2×1020次。2.566×107×108次,24×3.6×103秒
≈2.2×1020(次)=221.7024×1018=(2.566×24×3.6) × (107×108×103)数学生活(1)较大的数应用科学记数法
表示。
(2)单位应化统一。 1学生练习:1.运用同底数幂的乘法法则计算下列各式,并用幂的形式表示结果。12.下面的计算对吗?如果不对,应如何改正?错错错对17×103×7.64×104=5.348×108(米)= 53.48 在太空中的空间实验室和航天飞船都是高速运行的,速度达到每秒7×103米以上,在对接过程中,如果计算不准,就可能发生飞船相撞事故。我国载人航天工程第一个空间交会对接目标是一天(7.64×104秒)。 按这样的速度,空间实验室运行一天,共经过多少路程?= 53.48 ×107×103+4=(7×7.64)×(103×104)1.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
.3523 =2x 2325=2x22 × =Xm+3+2=x7m+3+2=72第三关1已知:am=2, an=3.求am+n =?解: am+n = am · an (同底数幂的乘法逆运用)
=2 × 3=6 第四关1计算代数式5a+2-5a的值。解:5a×52-5a5a+2-5a==25×5a-5a=24×5a×525a+21感悟点滴 在本堂课的学习中有什
么收获和感悟呢?
1§3.1同底数幂的乘法(1)一、同底数幂的乘法法则
1.法则:同底数幂相乘,底数不变,指数相加。3.应用法则时的注意事项:(1)底数必须相同;
(2) 相乘时底数没有发生变化;
(3)指数相加的和作为最终结果的指数;
(4)底数a可以是任意有理数,也可以是单项式或多项式;
(5)2.法则的推广:(1)
(2)二、同底数幂的乘法法则的逆用
法则:1【1】、复习、整理、巩固今天所学知识。一、必做题:1、作业本(1)第12--13页T1—T7;
2、参书第61--62页A组题T1—T4;
3.课时特训第33、34页T1—T16;
二、选做题:1、参书第62页B组题T5、T6;
2.拓展探究题:参看幻灯片第26--29号。
三、抄写第24张幻灯片的内容。【2】、书面作业布置作业:11.解答下列各题:拓展探究题11(1) (a-b)2×(b-a)解:原式= (a-b)2[-(a-b)]= -(a-b)3或 原式= (b-a)2(a-b)= (b-a)34.计算(2) (a-b)3(b-a)2方法一:解原式= (a-b)3(a-b)2=(a-b)5方法二:解原式= [-(b-a)3](b-a)2=-(b-a)5116.我们规定 ,例如:(1)试求12 4和3 7的值.
(2)想一想 与 相等吗?请你说明理由。1再见祝同学们 学习进步!11
年是指光经过一年所行
的距离,光的速度是
3.0×105千米/秒,若
一年以365天计,
则1光年大约是多少千米?3.0×105×3.65×102=(3.0×3.65)×(105×102)1瑞安市东山中学§3.1同底数幂的乘法(1)1 an 表示的意义是什么?其中a、n、an分 别叫做什么? an底数幂指数an = a × a × a ×… a
n个a
1问题(1) 23、22表示什么?
23 = ----------------.
22 = ----------------------------- 2×2×2(乘方的意义)回顾 探究2×2问题(2) 23 ×22表示什么? 2×2×2 2×22×2×2×2×2问题(3) 23 ×22该怎么算? 51探索 发现
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
= 5 × 5 × 5 × 5 × 5 × 5 × 5
=5723 ×2453×54=(2 ×2 ×2) ×(2 ×2 ×2 ×2)= 2 ×2 ×2 ×2 × 2 ×2 ×2(乘方的意义)(乘法结合律)(乘方的意义)(乘方的意义)(乘方的意义)(乘法结合律)1观察思考: (1)上面各题中等号左边的两个幂的底数有什么特点?
(2)观察上面各题等号左右两边,底数、指数有什么关系?
(1) 23×22 =( ) ×( )
= =2( )(2) 4× 3 =( ) ×( )
= = ( )(3) =( ) ×( )
= =5( )=23+22×2×22×22×2×2×2×2575×5×…×55×5×…×55×5×…×5请同学们先根据刚才的理解,填空1猜想: am · an= (m、n都是正整数) am · an =m个an个a= aa…a=am+n(m+n)个a(aa…a)(aa…a)am+n(乘方的意义)(乘法结合律)(乘方的意义)1am · an = am+n (m、n都是正整数)同底数幂相乘,底数 ,指数 。不变相加 同底数幂的乘法法则:条件:①同底数幂 ②幂的乘法
结果:①底数不变 ②指数相加1例1、计算下列各式,结果用幂的形式表示:
(1)78×73
(2)(-2)8×(-2)7
(3) a· a3 am · an = am+n
解:原式=78+3=711解:原式=(-2)8+7=(-2)15解:原式=a1+3=a4=-215同底数幂的乘法公式11 1.同底数幂 ,底数 ,指数 .不变相加相乘
2.???口答(A组): (2) a7 ×a(1) 105×105第一关( 4 )3×33( 5) x 3n+1 · x 2n-1( 6 ) a + a + a(3)(-3)2×(-3)31 b5 · b5= b10 b5 + b5 = 2b5 x2 · x3 = x5 a · a6 = a7× × ××(3)x2 ·x3 = x6 ( ) (5)a · a6 = a6 ( )下面的计算对不对?如果不对,怎样改正?(1)b5 + b5 = b10 ( ) (2)b5 · b5= 2b5( ) (4)73×78= 711( )√1(2) (-2)5×23(1) -28×27例2:注意观察下列各式,然后计算,结果用幂的形式表示:公式: am · an = am+n 解:原式= -( 28×27)=-215解:原式= - 25×23 =-(25×23 )=-28(3) (a-b)2×(a-b)解:原式= (a-b)2+1= (a-b)3若底数不同,先化为相同,后运用法则.
公式中的a可为一个有理数、单项式或多项式(整体思想)
1
2.???计算(B组): 解:原式=c5 × c6=c11 解:原式 =-b6 (3) c5 × (-c)6 (2) -b5 ×b 若底数不相同,应先化相同第二关 (1) 74 × (-7)3 解:原式= - 74 × 73
= - 77
1am · an · ap 等于什么?根据上面的知识进行计算:
b· b3· b5解: b· b3· b5
= b1+3+5
= b9
1例3我国“天河-1A”超级计算机的实测运算速度达到每秒2.566千万亿次。如果按这个速度工作一整天,那么它能运算多少次?解 2.566千万亿次= 24时=由乘法的交换律和结合律,得
(2.566×107×108)× (24×3.6×103)答:它一天约能运算2.2×1020次。2.566×107×108次,24×3.6×103秒
≈2.2×1020(次)=221.7024×1018=(2.566×24×3.6) × (107×108×103)数学生活(1)较大的数应用科学记数法
表示。
(2)单位应化统一。 1学生练习:1.运用同底数幂的乘法法则计算下列各式,并用幂的形式表示结果。12.下面的计算对吗?如果不对,应如何改正?错错错对17×103×7.64×104=5.348×108(米)= 53.48 在太空中的空间实验室和航天飞船都是高速运行的,速度达到每秒7×103米以上,在对接过程中,如果计算不准,就可能发生飞船相撞事故。我国载人航天工程第一个空间交会对接目标是一天(7.64×104秒)。 按这样的速度,空间实验室运行一天,共经过多少路程?= 53.48 ×107×103+4=(7×7.64)×(103×104)1.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
.3523 =2x 2325=2x22 × =Xm+3+2=x7m+3+2=72第三关1已知:am=2, an=3.求am+n =?解: am+n = am · an (同底数幂的乘法逆运用)
=2 × 3=6 第四关1计算代数式5a+2-5a的值。解:5a×52-5a5a+2-5a==25×5a-5a=24×5a×525a+21感悟点滴 在本堂课的学习中有什
么收获和感悟呢?
1§3.1同底数幂的乘法(1)一、同底数幂的乘法法则
1.法则:同底数幂相乘,底数不变,指数相加。3.应用法则时的注意事项:(1)底数必须相同;
(2) 相乘时底数没有发生变化;
(3)指数相加的和作为最终结果的指数;
(4)底数a可以是任意有理数,也可以是单项式或多项式;
(5)2.法则的推广:(1)
(2)二、同底数幂的乘法法则的逆用
法则:1【1】、复习、整理、巩固今天所学知识。一、必做题:1、作业本(1)第12--13页T1—T7;
2、参书第61--62页A组题T1—T4;
3.课时特训第33、34页T1—T16;
二、选做题:1、参书第62页B组题T5、T6;
2.拓展探究题:参看幻灯片第26--29号。
三、抄写第24张幻灯片的内容。【2】、书面作业布置作业:11.解答下列各题:拓展探究题11(1) (a-b)2×(b-a)解:原式= (a-b)2[-(a-b)]= -(a-b)3或 原式= (b-a)2(a-b)= (b-a)34.计算(2) (a-b)3(b-a)2方法一:解原式= (a-b)3(a-b)2=(a-b)5方法二:解原式= [-(b-a)3](b-a)2=-(b-a)5116.我们规定 ,例如:(1)试求12 4和3 7的值.
(2)想一想 与 相等吗?请你说明理由。1再见祝同学们 学习进步!11
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
