浙教版七年级数学下册 5.1分式 课件(共19张)
文档属性
| 名称 | 浙教版七年级数学下册 5.1分式 课件(共19张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 421.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-10 18:48:30 | ||
图片预览

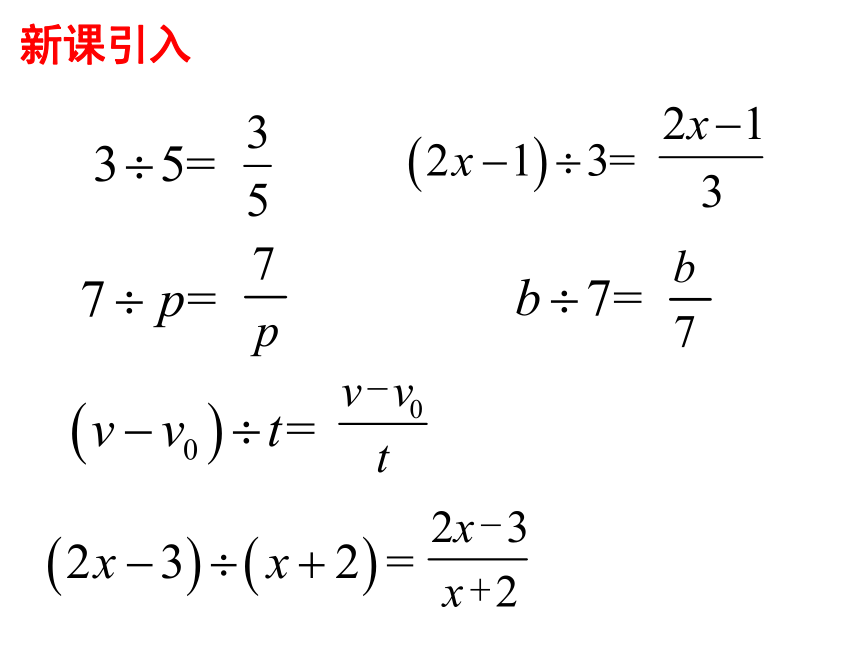





文档简介
(共19张PPT)
5.1 分 式
新课引入
新课引入
代 数 式
请将下列代数式进行分类,并说明你分类的理由.
整式
?
新课引入
概念
两个整式相除
除式中含有字母
表示 ,且 ,
像这样的代数式就叫做分式.
1.下列代数式中,哪些是整式?哪些是分式?
整式:
分式:
概念辨析
分式与整式有什么区别?
整式不一定有分母,若有分母,此分母中不含字母;
分式一定有分母,且分母中含有字母.
概念辨析
B
3.请从下列四个代数式中,任选两个,构造出一个分式.
3 , x-1 ,2x ,x2-1 .
概念辨析
分母为x-1:
分母为2x:
分母为x2-1:
分式再认识--关于字母的取值问题
问题:
分式中字母的取值不能使分母为零.
当分母的值为零时,
分式就没有意义,
分母a的值不能为“零”
分母的值不能为“零”
分母≠0
新知再识
例1 对于分式 .
(1)当x取什么数时,分式有意义?
(2)当x取什么数时,分式的值是零?
无
(3)当x=1时,分式的值是多少?
思考?
当x取什么数时,代数式的值为零?
新知巩固:
≠0
=2
=3
=2
小结
分式
概念
值为零
有意义
无意义
表示两个整式相除, 且除式中含有字母
分式应用
甲、乙两辆车都从A地出发返回B地,走相同路线.已知甲车每时行45千米,乙车每时行40千米,如果乙提前0.1小时出发,那么甲车追上乙车需要 小时.
返程路上疑问1
乙
甲
0.1小时
A
B
甲的路程=乙的路程
分式应用
例2. 甲﹑乙两人从一条公路的某处出发,同向而行.已知甲每时行a千米,乙每时行b千米,a>b.如果乙提前1小时出发,那么甲追上乙需要多少时间?
q
甲
乙
甲 乙
速度
时间
路程
a
b
x
1+x
ax
b+bx
当a=6,b=5时,求甲追上乙所需要时间.
例2. 甲﹑乙两人从一条公路的某处出发,同向而行.已知甲每时行a千米,乙每时行b千米,a>b.如果乙提前1小时出发,那么甲追上乙需要多少时间?
当a=6,b=5时,
结合实际想一想:
若取a=5,b=5,分式 有意义吗?它们表示的实际情景是什么?
拓展提升
学校作业:
1.完成作业本1 5.1分式
回家作业:
1.完成同步集训 5.1分式
2.预习 5.2 分式的基本性质
作业布置
5.1 分 式
新课引入
新课引入
代 数 式
请将下列代数式进行分类,并说明你分类的理由.
整式
?
新课引入
概念
两个整式相除
除式中含有字母
表示 ,且 ,
像这样的代数式就叫做分式.
1.下列代数式中,哪些是整式?哪些是分式?
整式:
分式:
概念辨析
分式与整式有什么区别?
整式不一定有分母,若有分母,此分母中不含字母;
分式一定有分母,且分母中含有字母.
概念辨析
B
3.请从下列四个代数式中,任选两个,构造出一个分式.
3 , x-1 ,2x ,x2-1 .
概念辨析
分母为x-1:
分母为2x:
分母为x2-1:
分式再认识--关于字母的取值问题
问题:
分式中字母的取值不能使分母为零.
当分母的值为零时,
分式就没有意义,
分母a的值不能为“零”
分母的值不能为“零”
分母≠0
新知再识
例1 对于分式 .
(1)当x取什么数时,分式有意义?
(2)当x取什么数时,分式的值是零?
无
(3)当x=1时,分式的值是多少?
思考?
当x取什么数时,代数式的值为零?
新知巩固:
≠0
=2
=3
=2
小结
分式
概念
值为零
有意义
无意义
表示两个整式相除, 且除式中含有字母
分式应用
甲、乙两辆车都从A地出发返回B地,走相同路线.已知甲车每时行45千米,乙车每时行40千米,如果乙提前0.1小时出发,那么甲车追上乙车需要 小时.
返程路上疑问1
乙
甲
0.1小时
A
B
甲的路程=乙的路程
分式应用
例2. 甲﹑乙两人从一条公路的某处出发,同向而行.已知甲每时行a千米,乙每时行b千米,a>b.如果乙提前1小时出发,那么甲追上乙需要多少时间?
q
甲
乙
甲 乙
速度
时间
路程
a
b
x
1+x
ax
b+bx
当a=6,b=5时,求甲追上乙所需要时间.
例2. 甲﹑乙两人从一条公路的某处出发,同向而行.已知甲每时行a千米,乙每时行b千米,a>b.如果乙提前1小时出发,那么甲追上乙需要多少时间?
当a=6,b=5时,
结合实际想一想:
若取a=5,b=5,分式 有意义吗?它们表示的实际情景是什么?
拓展提升
学校作业:
1.完成作业本1 5.1分式
回家作业:
1.完成同步集训 5.1分式
2.预习 5.2 分式的基本性质
作业布置
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
