3.3(1)多项式的乘法

课件30张PPT。瑞安市东山中学§3.3多项式的乘法(1)11.课前练习(1)(-x)3·(-x)3·(-x)5=______;
(2) (x2)4=_______;
(3) (x3y5)4=______; (4)(xy)3·(xy)4·(xy)5=______;
(5) (-3x3y)(-5x4y2z4)=_______;
(6)-3ab2(-4a+3ab-2)
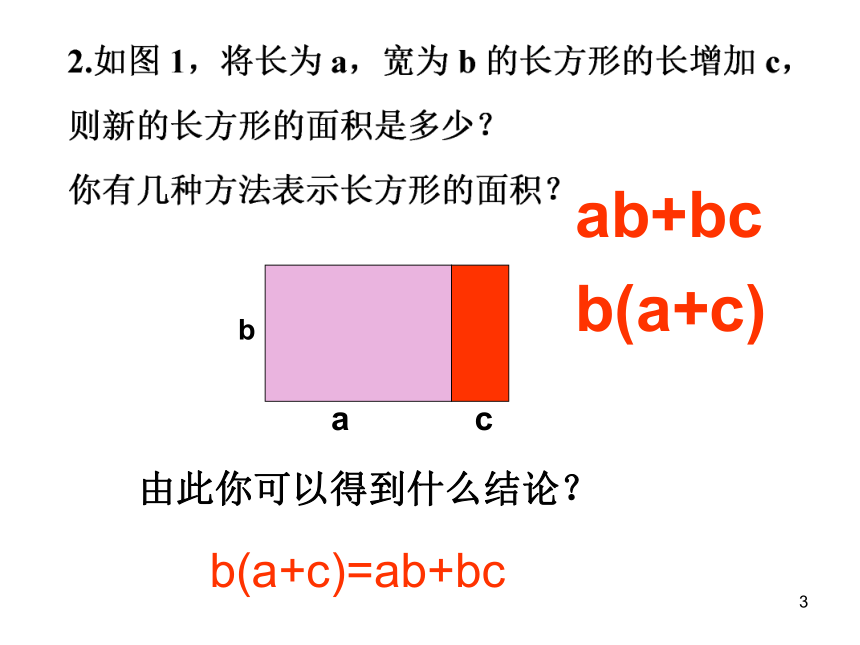
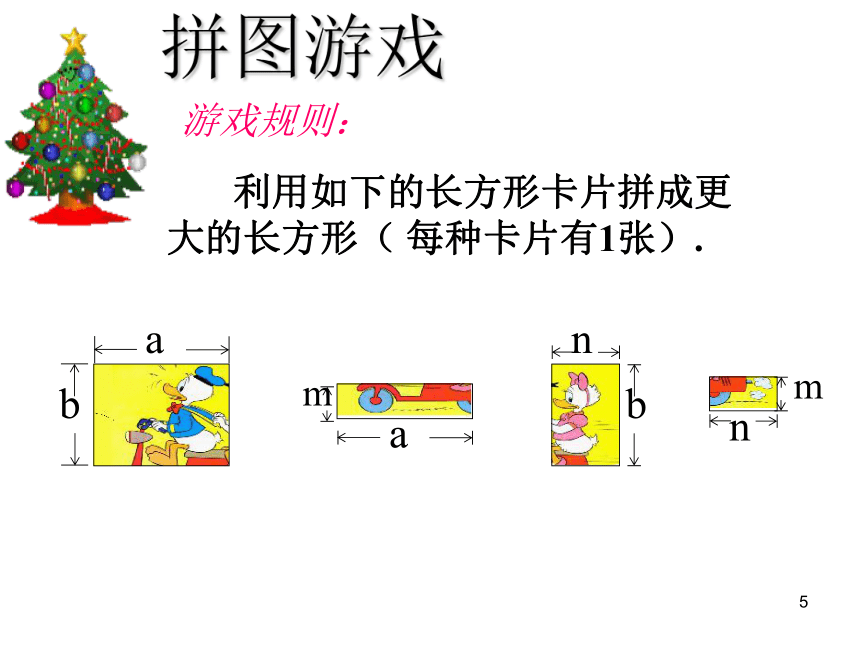
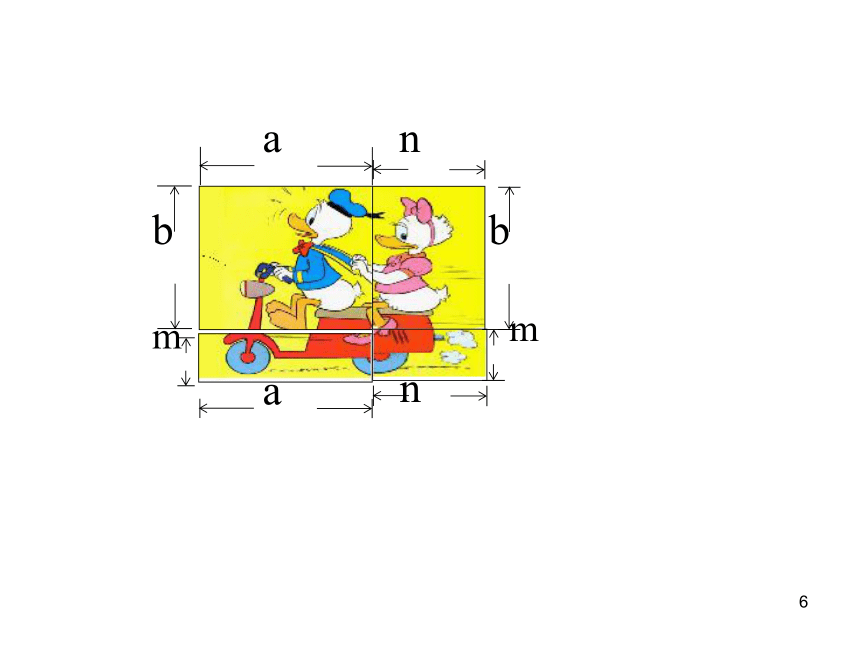
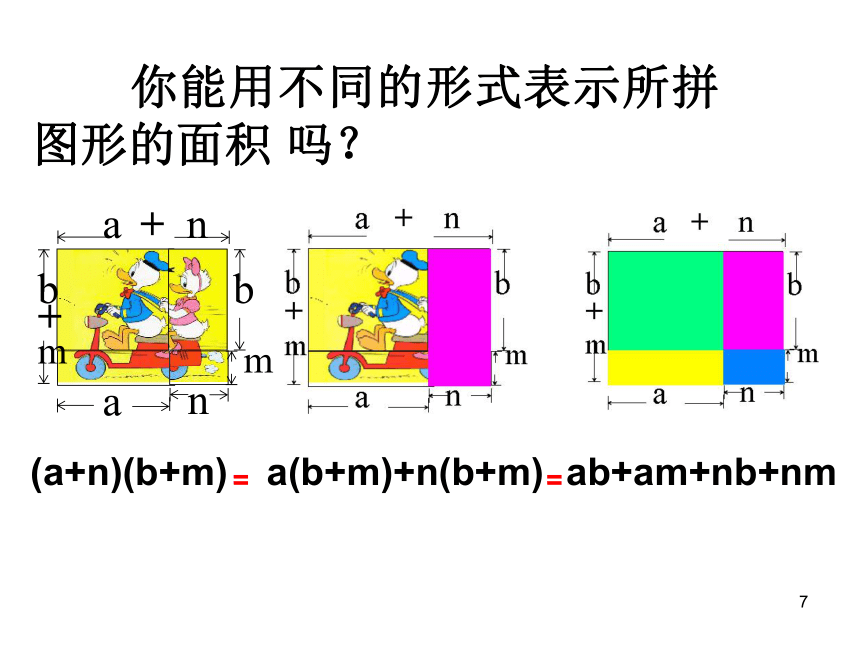
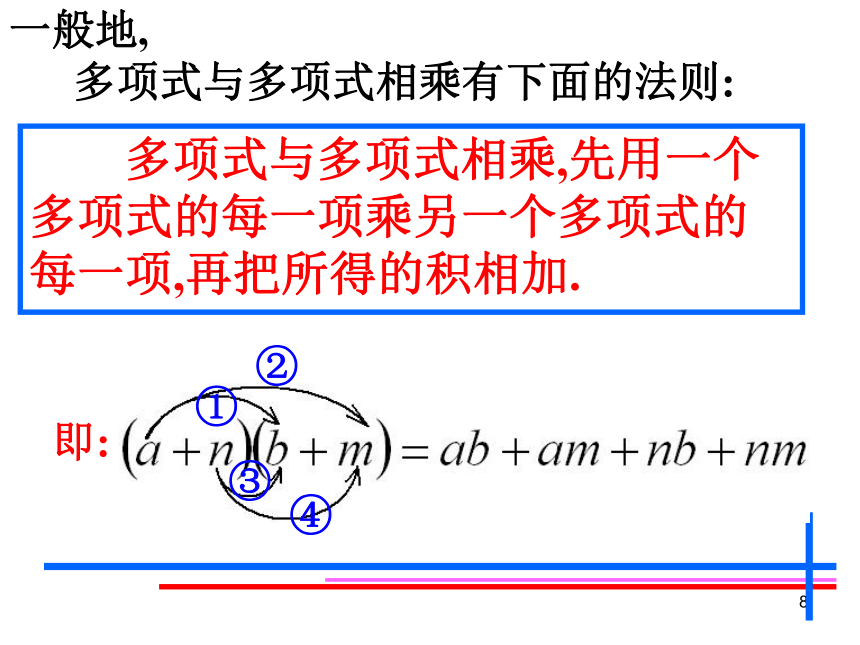
=________________-x11x8x12y20x12y1215x7y3z412a2b2-9a2b3+6ab21由此你可以得到什么结论？b(a+c)=ab+bcab+bcb(a+c)1回顾与思考单项式乘以多项式的 依据是: 乘法对加法的分配律.① 不能漏乘:即单项式要乘遍多项式的每一项.② 去括号时注意符号的确定.1拼图游戏11 你能用不同的形式表示所拼图形的面积 吗？(a+n)(b+m) a(b+m)+n(b+m) ab+am+nb+nm==1一般地,
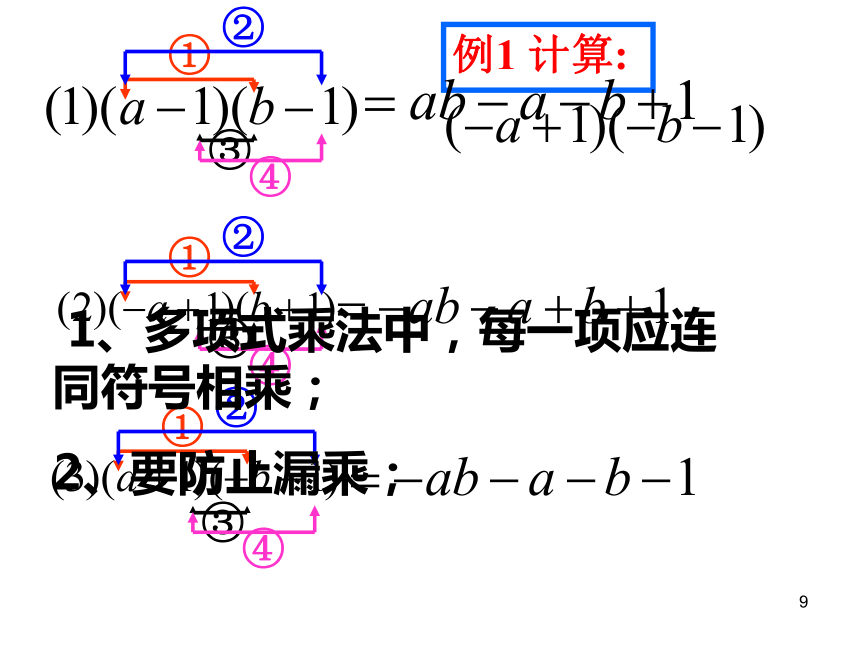
多项式与多项式相乘有下面的法则: 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.1例1 计算: 1、多项式乘法中，每一项应连同符号相乘；
2、要防止漏乘；1例2 计算: (3x-1)(x+3)3、多项式相乘的积在没有合并同类项前,所得的项数是两 个多项式项数的积；
4、乘积中，有同类项时一定要合并，得到最简结果。1 1、漏乘;2、符号问题; 3、最后结果应化成最简形式。1 注1：在合并同类项之前，展开式的项数恰好等于两个多项式的项数的积。1 注2：若含有与多项式的积差的运算，后两个多项式乘积的展开式要用括号括起来。1 注3：若含有数与多项式的积相乘的运算，
可先将多项式乘积展开，再用括号括起来1
加油哦！！展示风采
1
加油哦！！第二关：先化简，再求值：
(2x-1)(-3y)-(1-3x)(1+2y)，
其中x=2，y=1.展示风采
1(x + 2)(x + 3) = x2 + 5x + 6;
(x + 4)(x + 2) = x2 + 6x + 8;
(x + 6)(x + 5) = x2 + 11x + 30; 根据你发现的规律,你能快速写出下面
的结果吗? 你能说出与(x + a) (x + b)相等的
多项式吗? x2 + 8x + 15 你发现了什么?1规律：练习：用推导的公式计算：1你会解答吗? 若(a + m) (a – 2 ) = a2 + na – 6 对 a 的任
何值都成立，求m,n值。 m = 3 , n = 1 解: (a + m) (a – 2 ) = a2 -2a+ma-2m
= a2 +(m-2)a-2m
∴n=m-2,-2m=-61你会解方程吗？解：一元二次方程一元一次方程解方程：2x(x-3)-(x-3)(x+8)=x2+101知识回眸1§3.3多项式的乘法(1)
1.多项式的乘法法则：多项式与多项式相乘,先用一个多项式的
每一项乘另一个多项式的每一项,再把所得的积相加。2.多项式的乘法法则在运用时要注意的事项：
(1).运用多项式的乘法法则时，必须做到不重不漏.
(2).多项式与多项式相乘，仍得多项式.
(3).注意确定积中的每一项的符号，多项式中每一项都包含它前面
的符号，“同号得正，异号得负”.
(4).多项式与多项式相乘的展开式中，有同类项的，要合并同类项.3. 多项式的乘法法则具有一般性，对于项数较多的两个多项式相乘，法则仍然适用；4.多项式与多项式相乘，其积仍然是一个多项式，多项式与多项式
相乘的展开式中若有同类项的要合并同类项，在合并同类项之前，
积的项数等于两个多项式的项数之积；15.6.1【1】、复习、整理、巩固今天所学知识。一、必做题：1、作业本(2)第24--25页T1—T7；
2、参书第115页A组题T1—T4；
3.课时特训第65、66页T1—T16
二、选做题：1、参书第115页B、C组题T5、T6；
2.拓展探究题：参看幻灯片第25--29号。
三、抄写第22--23张幻灯片的内容。【2】、书面作业布置作业：1拓展探究题111
4.若(x+a)(x+b)中不含x的一次项,
则a与b的关系是 ( )
(A)a=b=0 (B)a-b=0
(C)a=b≠0 (D)a+b=0D拓展提升：1拓展提升：1同学们，再见！1