3.2单项式的乘法
图片预览







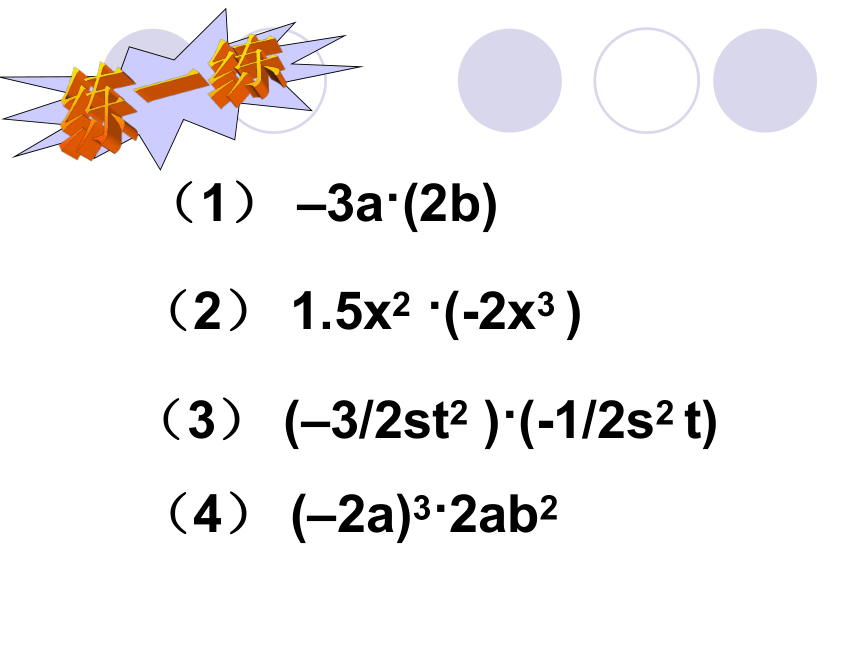
文档简介
课件22张PPT。3.2单项式的乘法一、创设情境,引出课题 同学们,你们到过北京天安门广场吗?它位于北京市中心,是世界上最大的城中广场,可容纳100万人。你们能想像它有多大吗?如果要估算天安门广场的面积,你会想用什么办法呢?
答:步测法、根据天安门广场的地图测量计算、上互联网查询资料等.二、引出新知,探究示例 探究活动一:现在有一位旅行者准备用步长测量天安门广场的面积。他先从南走到北,记下所走的步数为1100步;再从东走到西,记下所走的步数为625步,然后根据自己的步长来估算广场的面积。假设这位旅行者的步长为0.8m,那么广场的面积大约是多少 ?①②①②①其中第二种运算的依据是什么?答:其中第二种运算的依据是乘法交换律和结合律。②如果用字母a表示该旅行者的步长,你能用含a的代数式表示广场的面积吗?并且可以把这个代数式表达得更简单些吗?答:③通过解决上述问题,你认为两个单项式相乘应怎样运算?运算的依据是什么?答:总结:两个单项式相乘,根据乘法交换律和结合律,可以把它们的系数、同底数幂分别相乘.各因式的系数结合成一组相同的字母结合一起一个字母方法:单项式与单项式相乘,把它们的系数、同
底数幂分别相乘,其余字母连同它的指数不变,
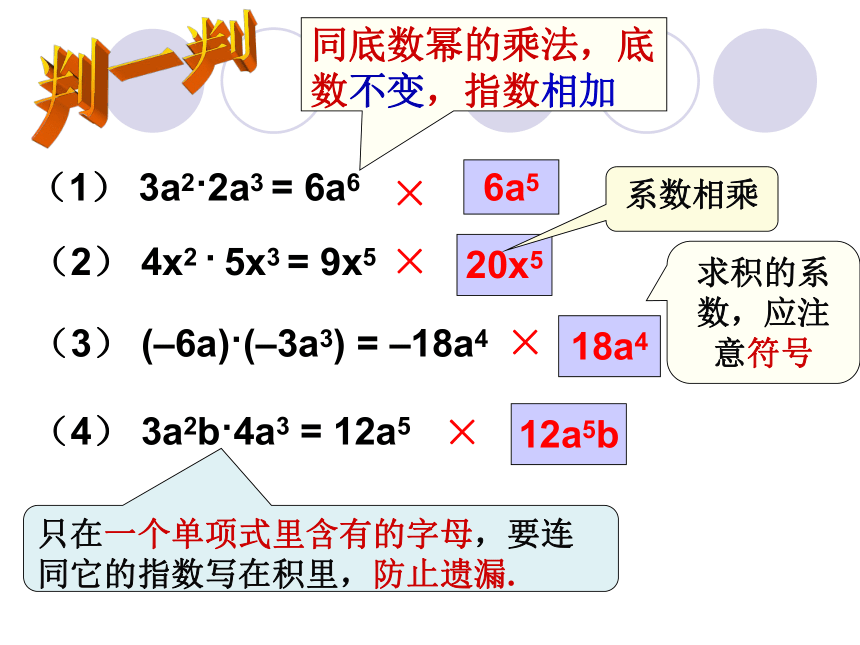
作为积的因式.大胆尝试单项式与单项式相乘的法则: 单项式与单项式相乘,把它们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式.例1:计算解:原式解:原式解:原式解:原式(5) -6a2b(x-y)3?2ab(x-y)2判一判 (1) 3a2?2a3 = 6a6 (2) 4x2 ? 5x3 = 9x5(3) (–6a)?(–3a3) = –18a4(4) 3a2b?4a3 = 12a5××××6a520x518a412a5b同底数幂的乘法,底数不变,指数相加求积的系数,应注意符号只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏.
系数相乘练一练(1) –3a?(2b)(3) (–3/2st2 )?(-1/2s2 t)(4) (–2a)3?2ab2(2) 1.5x2 ?(-2x3 )2、单项式与多项式的乘法.合作探索学习二:一幅电脑画的尺寸如图:mmab(1)请用两种不同的方法表示画面的面积;
(2)这两种不同的方法表示的面积应当相等,你能用运算律
解释它们相等吗?(3)通过上面的讨论,你能总结出单项式与多项式相乘的运算规律吗?答(1)(2) 单项式与多项式相乘的法则: 单项式与多项式相乘,就是用单项式去乘多项式的每一项,,再把所得的积相加.a(b+c)=ab+ac注意: 1.注意多项式中每一项的符号; 注意单项式的符号
2. 积为一个多项式,其项数与多项式的项数相同,
不要漏乘了项。
3.积的符号的确定实质是:同号得正,异号得负例2:计算解:原式=解:原式= 练习第3题
(1). -2(a-b+ c)(2). (x-3y)(-6x)(1) -m(a-b)=-ma-mb ( )(2) (a-3b)?(-6a)=-6a2-18ab ( )(3) (-x2y)(-9xy+1)=9x3y2+1( )(4) (2ab2-3ab)(-3ab)=-6a2b3+9a2b2 ( ) 判断下列计算是否正确,并简要说明理由.竞×××√大显身手填一填: (1) ( )?(3x2y2)=81x4y6(2) –3a2( –4ab+ )=–15a4+12a3b–3a227x2y4125a21(3) 若(my3)?(4yn)2=16y7
则m = , n = .
1、通过这节课的学习,你有哪些收获?有哪些困惑?
2、你有哪些感受?我学到了什么?小结作业: 1、复习、整理、巩固今天所学知识,(当天完成)
2、作业本(2)3.2 基础练习必做,希望完成综合运用.(当天上交)
3、课课练B3.2课后作业必做,当堂训练选做.(回家作业)
4、预习下一节课,选做课本作业题.(回家作业)转化转化实数运算幂的运算转 化单项式乘以单项式单项式乘以多项式(1)已知:
则m= a= b= (2) 已知
(m是小于10的自然数),则m= , n=___:挑战自我挑战自我已知:求 :的值。 如图:在一个长方形的公园修建一个草坪,如阴影所示.E是AB的中点,F是BC的三等份点.已知AB=2a,BC=3b.求草坪的面积.再见!
答:步测法、根据天安门广场的地图测量计算、上互联网查询资料等.二、引出新知,探究示例 探究活动一:现在有一位旅行者准备用步长测量天安门广场的面积。他先从南走到北,记下所走的步数为1100步;再从东走到西,记下所走的步数为625步,然后根据自己的步长来估算广场的面积。假设这位旅行者的步长为0.8m,那么广场的面积大约是多少 ?①②①②①其中第二种运算的依据是什么?答:其中第二种运算的依据是乘法交换律和结合律。②如果用字母a表示该旅行者的步长,你能用含a的代数式表示广场的面积吗?并且可以把这个代数式表达得更简单些吗?答:③通过解决上述问题,你认为两个单项式相乘应怎样运算?运算的依据是什么?答:总结:两个单项式相乘,根据乘法交换律和结合律,可以把它们的系数、同底数幂分别相乘.各因式的系数结合成一组相同的字母结合一起一个字母方法:单项式与单项式相乘,把它们的系数、同
底数幂分别相乘,其余字母连同它的指数不变,
作为积的因式.大胆尝试单项式与单项式相乘的法则: 单项式与单项式相乘,把它们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式.例1:计算解:原式解:原式解:原式解:原式(5) -6a2b(x-y)3?2ab(x-y)2判一判 (1) 3a2?2a3 = 6a6 (2) 4x2 ? 5x3 = 9x5(3) (–6a)?(–3a3) = –18a4(4) 3a2b?4a3 = 12a5××××6a520x518a412a5b同底数幂的乘法,底数不变,指数相加求积的系数,应注意符号只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏.
系数相乘练一练(1) –3a?(2b)(3) (–3/2st2 )?(-1/2s2 t)(4) (–2a)3?2ab2(2) 1.5x2 ?(-2x3 )2、单项式与多项式的乘法.合作探索学习二:一幅电脑画的尺寸如图:mmab(1)请用两种不同的方法表示画面的面积;
(2)这两种不同的方法表示的面积应当相等,你能用运算律
解释它们相等吗?(3)通过上面的讨论,你能总结出单项式与多项式相乘的运算规律吗?答(1)(2) 单项式与多项式相乘的法则: 单项式与多项式相乘,就是用单项式去乘多项式的每一项,,再把所得的积相加.a(b+c)=ab+ac注意: 1.注意多项式中每一项的符号; 注意单项式的符号
2. 积为一个多项式,其项数与多项式的项数相同,
不要漏乘了项。
3.积的符号的确定实质是:同号得正,异号得负例2:计算解:原式=解:原式= 练习第3题
(1). -2(a-b+ c)(2). (x-3y)(-6x)(1) -m(a-b)=-ma-mb ( )(2) (a-3b)?(-6a)=-6a2-18ab ( )(3) (-x2y)(-9xy+1)=9x3y2+1( )(4) (2ab2-3ab)(-3ab)=-6a2b3+9a2b2 ( ) 判断下列计算是否正确,并简要说明理由.竞×××√大显身手填一填: (1) ( )?(3x2y2)=81x4y6(2) –3a2( –4ab+ )=–15a4+12a3b–3a227x2y4125a21(3) 若(my3)?(4yn)2=16y7
则m = , n = .
1、通过这节课的学习,你有哪些收获?有哪些困惑?
2、你有哪些感受?我学到了什么?小结作业: 1、复习、整理、巩固今天所学知识,(当天完成)
2、作业本(2)3.2 基础练习必做,希望完成综合运用.(当天上交)
3、课课练B3.2课后作业必做,当堂训练选做.(回家作业)
4、预习下一节课,选做课本作业题.(回家作业)转化转化实数运算幂的运算转 化单项式乘以单项式单项式乘以多项式(1)已知:
则m= a= b= (2) 已知
(m是小于10的自然数),则m= , n=___:挑战自我挑战自我已知:求 :的值。 如图:在一个长方形的公园修建一个草坪,如阴影所示.E是AB的中点,F是BC的三等份点.已知AB=2a,BC=3b.求草坪的面积.再见!
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
