七年级数学下册3.4乘法公式(1)

课件39张PPT。13.4 乘法公式(一)平方差公式2 从前有一个狡猾的地主，他把一块长为a米的正方形的土地租给张老汉种植，有一天，他对张老汉说：“ 我把这块地的一边减少b米，另一边增加b米，继续租给你，你也没有吃亏，你看如何？” 张老汉一听觉得没有吃亏，就答应了 ，回到家中，他把这件事对儿子讲了，儿子一听，说：“爸爸你吃亏了！”，张老汉非常吃惊。
同学们，你想告诉张老汉这是为什么吗？小故事3
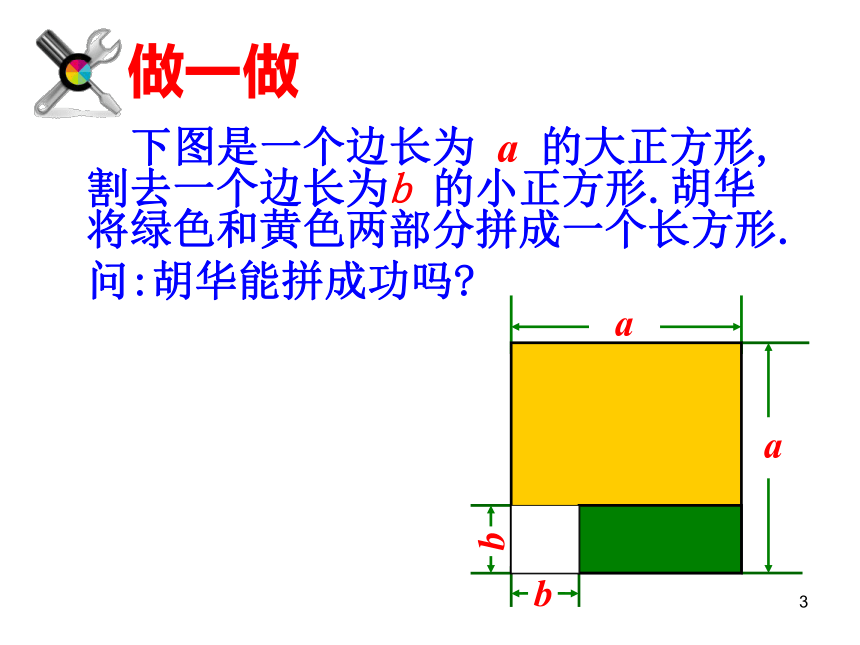
下图是一个边长为 a 的大正方形,割去一个边长为b 的小正方形.胡华将绿色和黄色两部分拼成一个长方形.
问:胡华能拼成功吗?
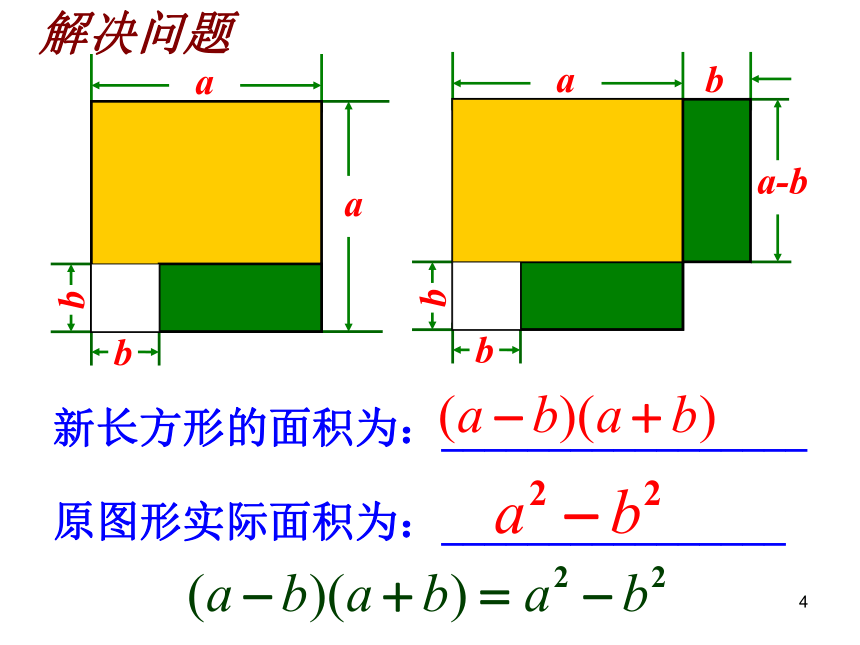
做一做4原图形实际面积为：________________新长方形的面积为：_________________bab解决问题5请先计算下列各题：6等式左边的两个多项式有什么特点？
②等式右边的多项式有什么规律？
(a+b)(a?b)=a2?b2两数和与这两数差的积,这两数的平方差.等于平方差公式：3.4乘法公式(1)7 例1 利用平方差公式计算：(3) (?4a3?1)(4a3?1)初步尝试:(1) (3x+5y)(3x-5y)=(3x)2-(5y)2= 9x2-25y2 (a + b)( a - b ) = a2 - b2公式中的a,b可以是数,还可以是单项式或多项式步骤：1、判断；2、调整；3、用公式。
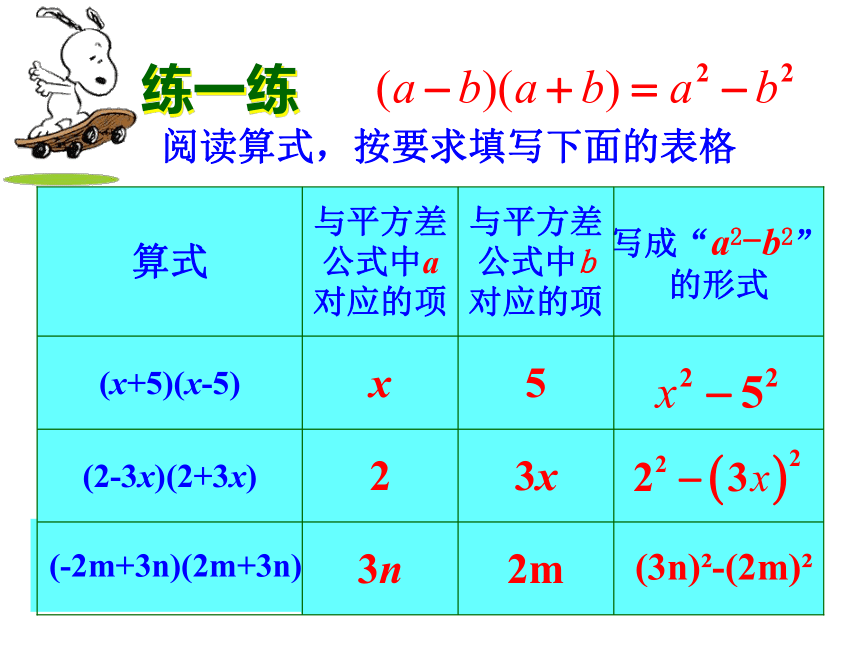
找出相等的“项”和符号相反的“项”，然后应用公式． 8练一练阅读算式，按要求填写下面的表格2m3n (-2m+3n)(2m+3n)3x2(2-3x)(2+3x)5x(x+5)(x-5)写成“a2-b2”的形式与平方差公式中b对应的项与平方差公式中a对应的项算式(3n)2-(2m)29抢答下列各题：
(l)(-a+b)(a+b)=??_________
(2)(a-b)(b+a)= __________
(3)(-a-b)(-a+b)= ________
??(4)(a-b)(-a-b)= _________a2-b2a2-b2b2-a2b2-a2(a+b)(a?b)=a2?b2你能用上面的规律直接计算下列各式吗？
10下列各式哪些可用平方差公式计算,
可用的算出它的结果。=y2 -x2 =y2 -x2 不可以可以可以不可以两个二项式相乘其中一项相同,另一项互为相反数,结果是相同项的平方减去相反数项的平方。=(y+x)( y-x)=(-y-x)(-y+x)火眼金睛顺口溜是：“相同项，相反项；符号判断来帮忙，
同平方，反平方；运算减号居中央”11
利用平方差公式计算（先确定各题的a与b再填空）
(1)(5+6x)(5-6x)=( )2-( )2=______
(2)(x-2y)(x+2y)=( )2-( )2=_______
(3)(-m+n)(-m-n)=( )2-( )2=_______
符号相同的项是a,符号相反的项是b56x25-36x2x2yx2-4y2-mnm2-n2①利用平方差公式计算的关键是__________
怎样确定a与b______________________来吧②当分数或是数与字母的乘积时,要用括号把这个数
整个括起来，最后的结果又要去掉括号。
准确确定a和b12例题精讲例2.运用平方差公式进行计算:13能力提高14例题3.下列两个多项式相乘，哪些可以用平方差公式？哪些不能？15学生练习：运用平方差公式计算：16 例题4.胡华同学去商店买了单价是9.8元/千克的糖果10.2千克，售货员刚拿起计算器，胡华就脱口说出99.96元，结果与售货员计算出的结果相吻合。售货员很惊讶地说：“你好象是个神童，怎么算得这么快？”胡华同学说：“过奖了，我利用了在数学上刚学过的一个公式。”
神童算账你知道胡华同学用的是什么公式吗？
怎么计算的吗?17让我想想我能行利用平方差公式计算:
(2+1)(22+1)(24+1)(28+1)+1=(2-1)(2+1)(22+1)(24+1)(28+1)+1=(22-1)(22+1)(24+1)(28+1)+1=21618 (1)103×97
(2) 59.8×60.2 你认为怎样计算更简单？19如果A=1234567892, B=123456788×123456790,
试比较A与B的大小.恐怕计数器也无奈20练一练21本节课你学到了什么?试用语言表述平方差公式 (a+b)(a?b)=x2?b2。应用平方差公式 时要注意一些什么？两数和与这两数差的积，等于它们的平方差。变成公式标准形式后，再用公式。运用平方差公式时，要紧扣公式的特征，
找出相等的“项”和符号相反的“项”，然后应用公式.要利用加法交换律，对于不符合平方差公式标准形式者，顺口溜是：“相同项，相反项；符号判断来帮忙，
同平方，反平方；运算减号居中央”22(3a +2b)(3a?2b) 9a2－4b2抢答题123(5ab+1)(5ab-1)25a2b2－1抢答题224(?0.1x+1)(?0.1x?1) 0.01x2－1抢答题32516k2 - 9抢答题426
(3y ? x)(? x ? 3y）抢答题527(-2x-y)(-y+2x)y2-4x2抢答题628抢答题729§3.4乘法公式(1)--平方差公式一、知识收获
1.平方差公式：两个数的和与这两个数的差的积等于这两个数
的平方差；二、能力收获
1.平方差公式的结构特征：
(1).左边是两个二项式相乘，并且这两个二项式中有一项完全相同，
另一项互为相反数；
(2).右边是乘式中两项的平方差(相同项的平方减去相反项的平方).
(3). 公式中的a、b具有广泛的含义，可以不是一个数，一个字母，
一个单项式，还可以表示一个多项式；2.运用平方差公式进行数的简便运算：根据相乘两数的形式特征，
把相乘的两数化成两数和与两数差的乘积形式；2.运用平方差公式的关键是识别两个项，哪个完全相同，哪个互为相反数；303. 公式的应用可以看成公式中字母取“值”的过程，关键是不要弄错.
刚开始使用公式时，运算格式可分两步，第一步先按公式特征写出
一个“框架”，如(a+b)(a-b)=( ) -( ) ；第二步在“框架”中填数计算；
利用平方差公式计算比利用多项式乘法法则计算简便得多，但是，
不符合平方差公式形式的两个二项式相乘，不能用平方差公式。224.平方差公式有八种变化形式：
(1)位置变化，
(8)逆运用公式变化，
(2)符号变化，(3)系数变化，(4)指数变化，(5)增项变化，(6)增因式变化，(7)连用公式变化，31【1】、复习、整理、巩固今天所学知识。一、必做题：1、作业本(1)第25--26页T1—T6；
2、参书第75页A组题T1—T4；
3.课时特训第45、46页T1—T18
二、选做题：1、参书第75--76页B、C组题T5--T7；
2.拓展探究题：参看幻灯片第32--38号。
三、抄写第29--30张幻灯片的内容。【2】、书面作业布置作业：322.已知x(x+5)-(-x+3)(-x-3)=19,求x的值。3.计算：拓展探究题334.若(N+1998) =65432178，求(N+1988) (N+2008)
的值。 2343536373839同学们，再见！