七年级数学下册3.4乘法公式(2)

课件37张PPT。13.4乘法公式(二)完全平方公式2公式的结构特征:左边是a2 ? b2两个二项式的乘积,平方差公式(a+b)(a?b)=即两数和与这两数差的积.右边是这两数的平方差.
(相同项)2-(相反项)2练习:用平方差公式计算:
(1)(-3x+4y)(-4y-3x)
(2)(x-2)(x2+4)(x+2)(x4+16)3改错题运用平方差公式计算:(1) (2x+1)(2x-1)(2)(3) (5m-3n)(5m+3n)(4) (-x+y)(-y-x)(5)4(a+b)(a+b)2ab=++ab瑞安市万松公园有一个边长为a的正方形
园地，为种植不同的花卉，将其边长增加
了b，形成4个种植花卉的区域，以种植不
同品种的花卉，请你用不同的方法计算这
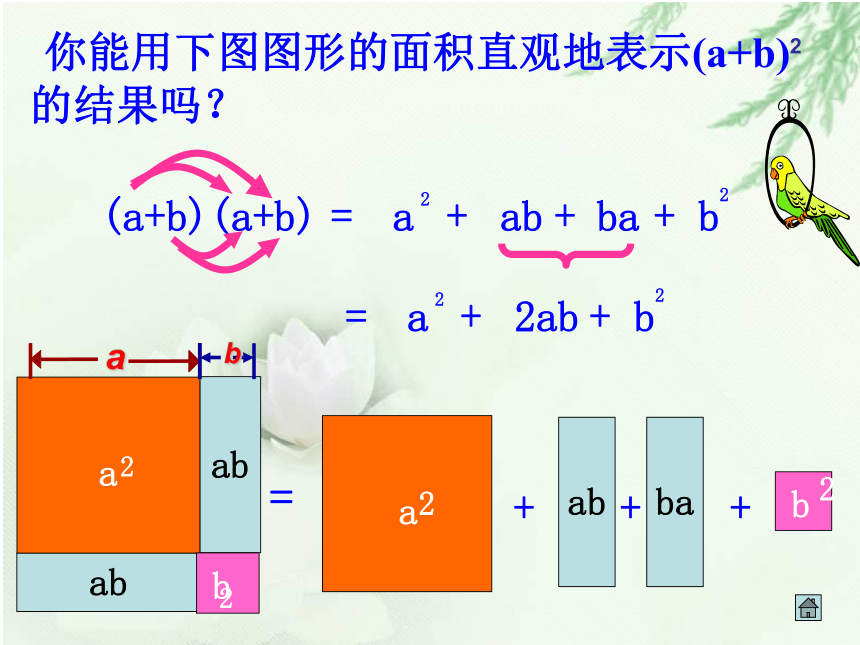
个园地的面积。2345(a+b)(a+b)abba=+++=abba+++ 你能用下图图形的面积直观地表示(a+b) 的结果吗？26 运用多项式与多项式相乘的法则计算下列各式：1、(a+b)23、(2a+x)2 观察上述1、2两题的计算结果，你发现有什么规律？你能用你的发现来猜测第3题的结果吗？合 作 学 习=(a+b)(a+b)2、(2+x)2 =(2+x)(2+x)= 22+2x+2x+x2=(2a)2+2×2a?x+x2=a2+ab+ab+b27 两数和的平方,等于这两数的平方和 , 加上这两数积的2倍. (a+b)2=a2+2ab+b28(2)(2a+3b)2= ( )2 + 2( )( ) + ( )2(a + 1)2=( )2+2( )( )+ ( )2aa112a2a3b3b用两数和的完全平方公式计算(填空):(a + b)2 = a2 + 2 a b + b29 你能用两数和的完全平方公式来计算(a?b)2吗?自主探索 ?=a2?2a b+b2=a2+2a (?b)+ (?b)2(a?b)2 =[a+(?b)]210 两数差的平方,等于这两数的平方和,减去这两数积的2倍. (a?b)2=a2?2ab+b211a2ababb2(a+b)2 =a?ba?bb(a?b)(a?b)2a2+2ab+b2即 (a?b)2 = a2?2ab+b2(a?b)2 = a2? ab ? b(a?b)　　　　　　试一试
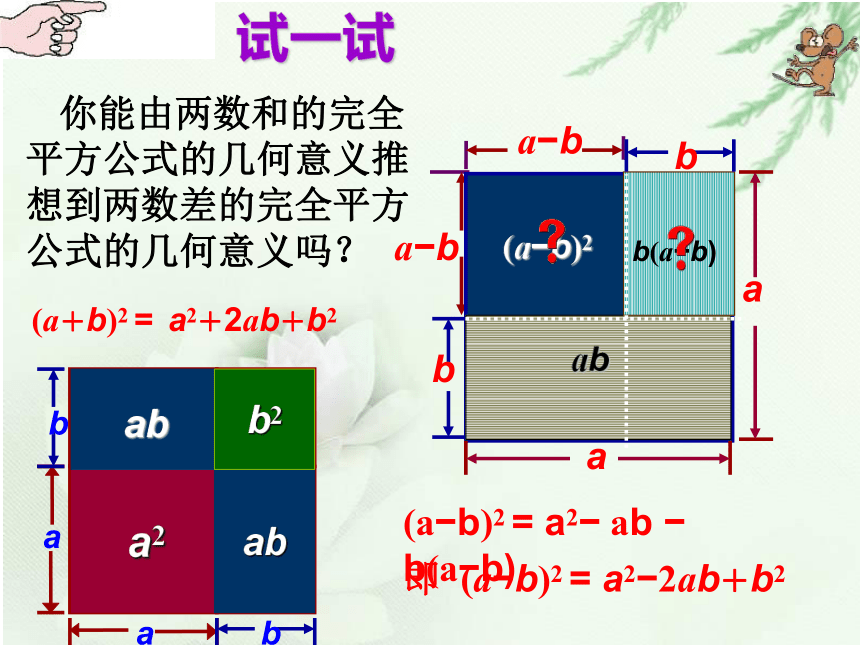
　你能由两数和的完全平方公式的几何意义推想到两数差的完全平方公式的几何意义吗？12完全平方公式 平方差公式和完全平方公式也称乘法公式。13 (a+b)2=a2+2ab+b2(a?b)2=a2?2ab+b2完全平方公式 两个数的和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的2倍。首平方，尾平方，首尾两倍放中间14运用规律填表－－15由表格可得：首尾平方总得正；
中间符号看首尾项的积，同号得正，
异号得负，中间的2倍要记牢；
进而总结步骤为：(1)、确定首尾，分别平方；
(2)、确定中间项的系数和
符号；
(3)、写出结论。16( x )2 + 2 ? x ? 2y +(2y)2解：(2) (x+2y)2 = 例1 利用完全平方公式计算：
(2a－5)2 ； (2) (x+2y)2;
(3) (－2s+t)2; (4) (－3x－4y)2x2=+4xy+4y2(1)( a ? b )2 = a2 ? 2 a b + b2( 2 a ?5 )2=(2a)2?2·2a· 5+52= 4 a2_ 20a+2517下列各式的计算错在哪里？应怎样改正？(1) (x+y)2 = x2 +y2(2) (a –b)2 = a2 -b2(4) (a+2b)2 = a2+2ab+2b2(3) (x– 1)2 = x2 – 2x (5) (2+x)2 = 2 + 4x+ x218请你直接应用完全平方公式计算：
1、（3+x)2 2、（y—7)2
3、（—2x—3y)2 4、（3— )2
19选择适当的公式计算：（1）、（2x—1）（—1+2x）
（2）、（—2x—y）（2x—y）
（3）、 （—a+5）（—a—5）
（4）、（ab—1）（—ab+1）201、运用完全平方公式计算：992
活用公式:2、如果x2-6x+N是一个完全平方式,那么N是( )
(A)36 (B)9 (C)-36 (D)-93、用简便的方法计算:
1.232+2.46×0.77+0.772 (4)已知(a+b)2=11,ab=1,求(a-b)2的值.21例题2.生活在线：一花农有1块正方形茶花苗圃，边长为am。现将这块苗圃的边长都增加1.5m，求这块苗圃的面积增加了多少m2。(a+1.5)2-a2=a2+3a+2.25-a2= 3a+2.2522练习1. 一花农有2块正方形茶花苗圃,
边长分别为 30.1 m , 29.5 m, 现将这2
块苗圃的边长都增加1.5m后,求各苗
圃的面积分别增加了多少m2?解：设原正方形苗圃的边长为a(m),
边长增加1.5m后,新正方形的边长
为(a+1.5)m；由题意可得，当a=30.1时，3a+2.25=3×30.1+2.25=92.55；
当a=29.5时，3a+2.25=3×29.5+2.25=90.75；
答：两块苗圃的面积分别增加了92.55平方米，90.75平方米。23练一练24例3.解下列各题：1.先化简再求值.2.已知a+b=4，ab=3,求下列代数式的值。2526例题例4：利用完全平方公式计算：
(1) 0.982 (2) 10012解：(1) 原式 = （ 1 ? 0.02）2= 12 ? 2 ×1×0.02 + 0.022= 1 ? 0.04 + 0.0004= 0.9604（2）原式 = （ 1000 + 1 ）2= 10002 + 2 × 1000×1 + 12= 1000000 + 2000 + 1=100200127探究练习1.如果 是一个完全平方式，那么a的值是()
A.2 B.-2 C. 2 D. 1CDA28本节课你学到了什么?注意完全平方公式和平方差公式不同： 完全平方公式的结果 是三项，即
(a ± b)2＝a2 ± 2ab + b2. 平方差公式的结果 是两项，即
(a+b)(a?b)＝a2?b2. 有时需要进行变形，使变形后的式子符合应
用完全平方公式的条件，即为“两数和(或差)的平方”，然后应用公式计算. 在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2.29§3.4乘法公式(2)--完全平方公式2.完全平方公式的结构特征：(1)公式左边是两个相同的二项式的积，
即两个数的和(或差)的平方；
(2)公式右边是一个三项式，其中两项是左边的二项的平方和，第三
项是左边两项的积的2倍；
(3)公式中的字母具有一般性，它可以表示数，也可以表示单项式
或多项式；1.完全平方公式：两数和或差的平方等于这两数的平方和加上或减去这两数积的2倍；即一、知识收获301.在运用公式时要注意分清是哪两个数(或式)的和，还是哪两个数(或式)的差；当所给的二项式各项符号相同，则用“和”的完全平方公式；当所给的二项式各项符号相反，则用“差”的完全平方公式；
2.
3.切勿把“乘积项”2ab中的2丢掉；
4. 二、能力收获31【1】、复习、整理、巩固今天所学知识。一、必做题：1、作业本(2)第16--19页T1—T7；
2、参书第78页A组题T1—T3；
3.课时特训第47、48页T1—T16；
二、选做题：1、参书第78页B、C组题T4—T6；
2.拓展探究题：参看幻灯片第32--36号。
三、抄写第20--30张幻灯片的内容。【2】、书面作业布置作业：32拓展探究题1.如图所示，它是由四个形状大小
完全相同的长方形拼成的图形，利
用面积的不同表示法，写出一个代
数恒等式2.先化简，再求值3334353637同学们，再见！