6.2 条形统计图和折线统计图 同步练习(含答案)
文档属性
| 名称 | 6.2 条形统计图和折线统计图 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-16 13:56:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
6.2 条形统计图和折线统计图
知识点 1 条形统计图和折线统计图
1.要反映某市某一周每天的最高气温的变化趋势,宜采用 ( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.以上都可以
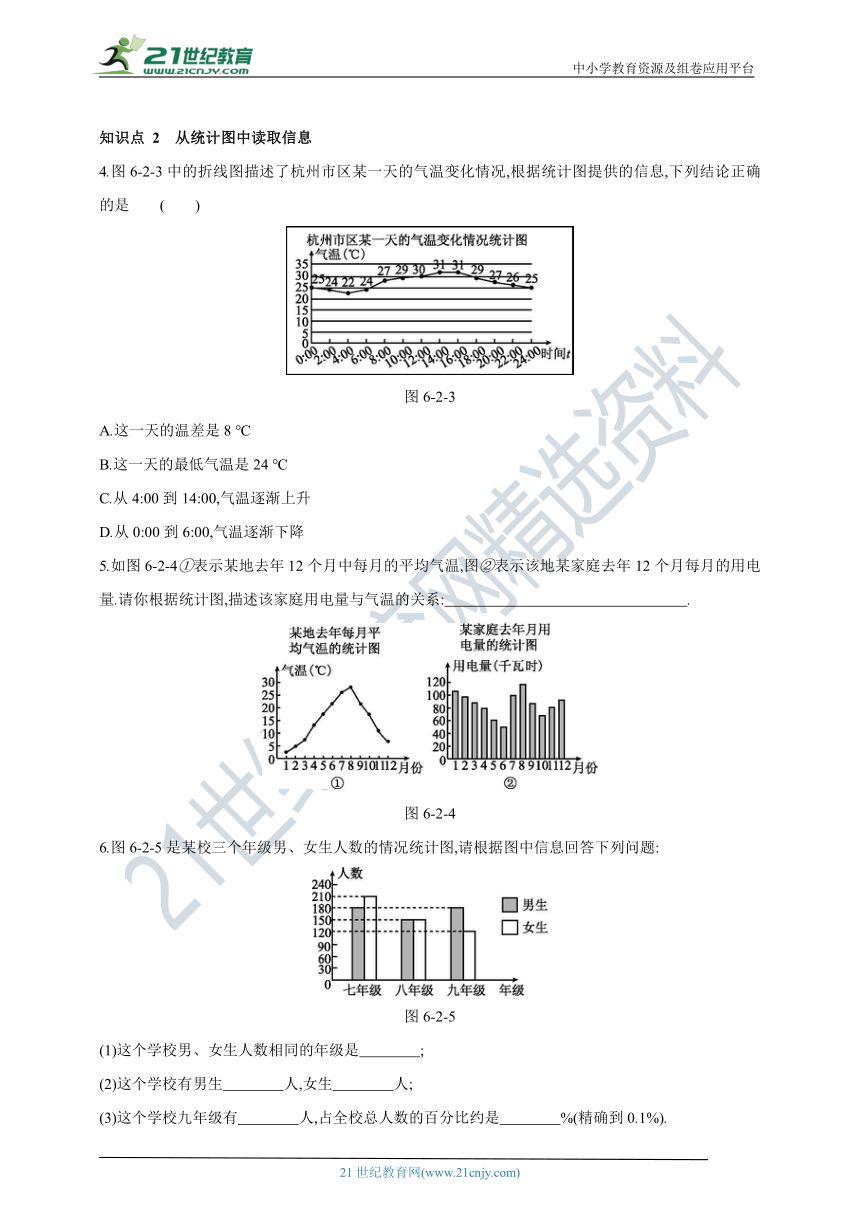
2.明明家今年1~5月份的用电量情况如图6-2-1所示,则相邻两个月用电量变化最大的是 ( )
A.1月至2月 B.2月至3月
C.3月至4月 D.4月至5月
图6-2-1
3.向阳中学七(6)班就上学方式作出调查后绘制了条形统计图如图6-2-2所示,那么乘车上学的人数是 ( )
图6-2-2
A.8 B.16 C.24 D.48
知识点 2 从统计图中读取信息
4.图6-2-3中的折线图描述了杭州市区某一天的气温变化情况,根据统计图提供的信息,下列结论正确的是 ( )
图6-2-3
A.这一天的温差是8 ℃
B.这一天的最低气温是24 ℃
C.从4:00到14:00,气温逐渐上升
D.从0:00到6:00,气温逐渐下降
5.如图6-2-4①表示某地去年12个月中每月的平均气温,图②表示该地某家庭去年12个月每月的用电量.请你根据统计图,描述该家庭用电量与气温的关系: .
图6-2-4
6.图6-2-5是某校三个年级男、女生人数的情况统计图,请根据图中信息回答下列问题:
图6-2-5
(1)这个学校男、女生人数相同的年级是 ;
(2)这个学校有男生 人,女生 人;
(3)这个学校九年级有 人,占全校总人数的百分比约是 %(精确到0.1%).
7.已知A,B两家酒店2021年下半年的月营业额折线统计图如图6-2-6,下列说法错误的是 ( )
图6-2-6
A.A酒店这半年的营业总额是13.8百万元
B.B酒店这半年的月营业额的最大值是3.6百万元
C.A酒店这半年的月营业额一直保持增长状态
D.B酒店这半年的月营业额11月至12月的增长率最大
8.某校九年级进行体育模拟考试,现从中随机抽取部分学生的体育成绩进行分段(A:50分;B:49~45分;C:44~40分;D:39~35分;E:34~0分),已知C等级人数占20%.请根据图6-2-7中信息回答下列问题:
图6-2-7
(1)抽取的样本中,样本容量是 ,A等级的人数为 人,并补全条形统计图;
(2)请估算该校900名九年级学生的体育模拟考试成绩在A,B两个分数段的共有多少人.
9.(2021丽水期末)某校举办七年级数学素养大赛,比赛共设三个项目:速算比赛、数学推理、巧解方程,每个项目得分都按一定百分比折算后计入总分.甲、乙、丙三位同学的速算比赛得分均为85分,且此项在总分中所占百分比不变,其余两项得分如图6-2-8所示(单位:分).
(1)根据图中信息判断哪位同学的总分最低
(2)甲、丙两同学的数学推理与巧解方程两项经折算后的得分和均为52分,求这两项在计入总分时所占的百分比;
(3)写出三个项目各项所占百分比的一组值,使甲或丙同学能获得第一名.
图6-2-8
详解详析
1.C [解析] 因为条形统计图能清楚地表示出每个项目的具体数目,折线统计图表示的是事物的变化情况,所以要反映某市某一周每天的最高气温的变化趋势,宜采用折线统计图.
故选C.
2.A
3.C [解析] 由条形统计图可知,乘车上学的人数是24.故选C.
4.C
5.当气温越高或越低时,该家庭用电量就越多
6.(1)八年级 (2)510 480
(3)300 30.3
[解析] (1)可直接从统计图中获得;(2)由统计图可知男生人数为180+150+180=510(人),女生人数为210+150+120=480(人);(3)九年级人数为180+120=300(人),全校总人数为510+480=990(人),300÷990×100%≈30.3%.
7.A
8.解:(1)60÷20%=300(人),因此,样本容量是300.
A等级的人数为300-110-60-30-10=90(人).
补全条形统计图如图.
(2)在A,B两个分数段的约有×900=600(人).
答:该校900名九年级学生的体育模拟考试成绩在A,B两个分数段的共约有600人.
9.解:(1)由题意得,甲、乙、丙三位同学的速算比赛得分相等,据图所知,乙同学的数学推理、巧解方程得分均最低,所以乙同学的总分最低.
(2)设数学推理在计入总分时所占的百分比为x,巧解方程在计入总分时所占的百分比为y.
根据题意,得
解得
0.2=20%,0.4=40%.
答:数学推理在计入总分时所占的百分比为20%,巧解方程在计入总分时所占的百分比为40%.
(3)因为甲、丙同学的速算比赛得分相等,且此项在总分中所占百分比不变,即40%,当数学推理占比为20%,巧解方程占比为40%时,甲、丙两同学的数学推理与巧解方程两项经折算后的得分和相等,甲同学的数学推理得分高,丙同学的巧解方程得分高,
所以若要使甲同学获得第一名,则应使数学推理在计入总分时所占的百分比大于20%,小于60%即可;若要使丙同学获得第一名,则应使巧解方程在计入总分时所占的百分比大于40%,小于60%即可,
所以甲同学获得第一名:速算比赛占比为40%,数学推理占比为40%,巧解方程占比为20%(答案不唯一);
丙同学获得第一名:速算比赛占比为40%,数学推理占比为10%,巧解方程占比为50%(答案不唯一).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
6.2 条形统计图和折线统计图
知识点 1 条形统计图和折线统计图
1.要反映某市某一周每天的最高气温的变化趋势,宜采用 ( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.以上都可以
2.明明家今年1~5月份的用电量情况如图6-2-1所示,则相邻两个月用电量变化最大的是 ( )
A.1月至2月 B.2月至3月
C.3月至4月 D.4月至5月
图6-2-1
3.向阳中学七(6)班就上学方式作出调查后绘制了条形统计图如图6-2-2所示,那么乘车上学的人数是 ( )
图6-2-2
A.8 B.16 C.24 D.48
知识点 2 从统计图中读取信息
4.图6-2-3中的折线图描述了杭州市区某一天的气温变化情况,根据统计图提供的信息,下列结论正确的是 ( )
图6-2-3
A.这一天的温差是8 ℃
B.这一天的最低气温是24 ℃
C.从4:00到14:00,气温逐渐上升
D.从0:00到6:00,气温逐渐下降
5.如图6-2-4①表示某地去年12个月中每月的平均气温,图②表示该地某家庭去年12个月每月的用电量.请你根据统计图,描述该家庭用电量与气温的关系: .
图6-2-4
6.图6-2-5是某校三个年级男、女生人数的情况统计图,请根据图中信息回答下列问题:
图6-2-5
(1)这个学校男、女生人数相同的年级是 ;
(2)这个学校有男生 人,女生 人;
(3)这个学校九年级有 人,占全校总人数的百分比约是 %(精确到0.1%).
7.已知A,B两家酒店2021年下半年的月营业额折线统计图如图6-2-6,下列说法错误的是 ( )
图6-2-6
A.A酒店这半年的营业总额是13.8百万元
B.B酒店这半年的月营业额的最大值是3.6百万元
C.A酒店这半年的月营业额一直保持增长状态
D.B酒店这半年的月营业额11月至12月的增长率最大
8.某校九年级进行体育模拟考试,现从中随机抽取部分学生的体育成绩进行分段(A:50分;B:49~45分;C:44~40分;D:39~35分;E:34~0分),已知C等级人数占20%.请根据图6-2-7中信息回答下列问题:
图6-2-7
(1)抽取的样本中,样本容量是 ,A等级的人数为 人,并补全条形统计图;
(2)请估算该校900名九年级学生的体育模拟考试成绩在A,B两个分数段的共有多少人.
9.(2021丽水期末)某校举办七年级数学素养大赛,比赛共设三个项目:速算比赛、数学推理、巧解方程,每个项目得分都按一定百分比折算后计入总分.甲、乙、丙三位同学的速算比赛得分均为85分,且此项在总分中所占百分比不变,其余两项得分如图6-2-8所示(单位:分).
(1)根据图中信息判断哪位同学的总分最低
(2)甲、丙两同学的数学推理与巧解方程两项经折算后的得分和均为52分,求这两项在计入总分时所占的百分比;
(3)写出三个项目各项所占百分比的一组值,使甲或丙同学能获得第一名.
图6-2-8
详解详析
1.C [解析] 因为条形统计图能清楚地表示出每个项目的具体数目,折线统计图表示的是事物的变化情况,所以要反映某市某一周每天的最高气温的变化趋势,宜采用折线统计图.
故选C.
2.A
3.C [解析] 由条形统计图可知,乘车上学的人数是24.故选C.
4.C
5.当气温越高或越低时,该家庭用电量就越多
6.(1)八年级 (2)510 480
(3)300 30.3
[解析] (1)可直接从统计图中获得;(2)由统计图可知男生人数为180+150+180=510(人),女生人数为210+150+120=480(人);(3)九年级人数为180+120=300(人),全校总人数为510+480=990(人),300÷990×100%≈30.3%.
7.A
8.解:(1)60÷20%=300(人),因此,样本容量是300.
A等级的人数为300-110-60-30-10=90(人).
补全条形统计图如图.
(2)在A,B两个分数段的约有×900=600(人).
答:该校900名九年级学生的体育模拟考试成绩在A,B两个分数段的共约有600人.
9.解:(1)由题意得,甲、乙、丙三位同学的速算比赛得分相等,据图所知,乙同学的数学推理、巧解方程得分均最低,所以乙同学的总分最低.
(2)设数学推理在计入总分时所占的百分比为x,巧解方程在计入总分时所占的百分比为y.
根据题意,得
解得
0.2=20%,0.4=40%.
答:数学推理在计入总分时所占的百分比为20%,巧解方程在计入总分时所占的百分比为40%.
(3)因为甲、丙同学的速算比赛得分相等,且此项在总分中所占百分比不变,即40%,当数学推理占比为20%,巧解方程占比为40%时,甲、丙两同学的数学推理与巧解方程两项经折算后的得分和相等,甲同学的数学推理得分高,丙同学的巧解方程得分高,
所以若要使甲同学获得第一名,则应使数学推理在计入总分时所占的百分比大于20%,小于60%即可;若要使丙同学获得第一名,则应使巧解方程在计入总分时所占的百分比大于40%,小于60%即可,
所以甲同学获得第一名:速算比赛占比为40%,数学推理占比为40%,巧解方程占比为20%(答案不唯一);
丙同学获得第一名:速算比赛占比为40%,数学推理占比为10%,巧解方程占比为50%(答案不唯一).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
