3.5整式的化简

课件29张PPT。13.5整式的化简瑞安市东山中学2复习引入(am)n=amn(ab)n=anbn3如图，点M是AB的中点，点P在MB上，分
别以AP，PB为边，作正方形APCD和正方
形PBEF.设AB=4a，MP=b，正方形APCD
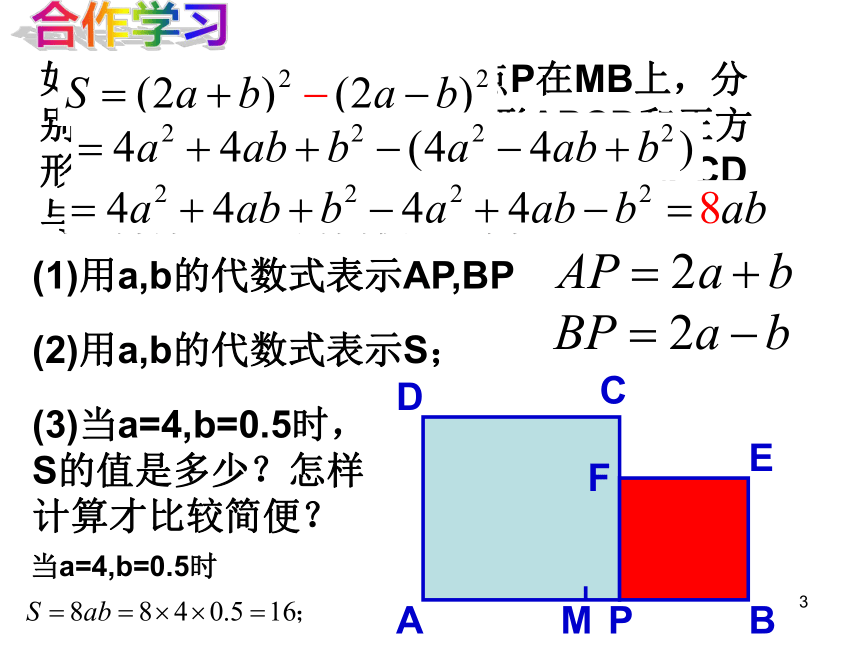
与正方形PBEF的面积之差为S.合作学习(2)用a,b的代数式表示S；(3)当a=4,b=0.5时，S的值是多少？怎样计算才比较简便？(1)用a,b的代数式表示AP,BP当a=4,b=0.5时4 整式的化简应遵循先乘方、再乘、
最后算加减的顺序。整式化简的运算顺序：能运用乘法公式的则运用公式。5例1、化简
（1）（2x－1)(2x＋1）－（4x＋3)(x－6）
（2）（2a＋3b）2－4a（a＋3b＋1）解：（1）原式==4x2 －1 －=4x2 －1 －(4x2 －21x －18)=4x2 －1 －4x2 +21x +18=21x +17（2）原式==4a2+12ab+9b2=9b2 －4a(4x2 －24x+3x －18)－4a2 － 12ab － 4a例题讲解6（1）先观察所要化简的整式，其中含有哪
些运算？确定运算的顺序。（2）各种运算应遵循怎样的运算法则？乘法
公式是否适用？（3）结果的形式应保持最简，有同类项的必须
合并同类项。注意：7练一练：化简下列各式(1) (x+6)2+(3+x)(3-x)(2) 3x(x2+3x+8)+(-3x-4)(3x-4)(3) (2x-5y)(2x+5y)-(2x+y)2(1)12x+45
(2)3x3+24x+16 (3)-26y2-4xy8填一填 一块手表原价100元，降价10％，
则现价为_____元。902. 一块手表原价a元，降价x％，则
现价为_______元。a(1-x％)3. 一块手表原价a(1-x％)元，降价x％，则现价为_________元。a(1-x％)29想一想1. 一块手表原价a元，涨价x％，则
现价为_________元。a(1+x％)2. 一块手表原价a元，连续两次涨价
x％，则现价为_________元。a(1+x％)210 例题2.甲、乙两家超市3月份的销售额均为a万元，在4月和5月这两个月中，甲超市的销售额平均每月增长x%，而乙超市的销售额平均每月减少x%。
（1）5月份甲超市的销售额比乙超市多多少？
（2）如果a=150，x=2，那么5月份甲超市的销售额
比乙超市多多少万元？瑞安大润发超市11实际应用 a a a(1＋x%) a(1－x%) a(1＋x%) (1＋x%)
= a(1＋x%)2 a(1－x%) (1－x%) = a(1－x%)2 太好了！我们一起努力。 甲、乙两家超市3月份的销售额均为a万元，在4月和5月这
两个月中，甲超市的销售额平均每月增长x%，而乙超市的
销售额平均每月减少x%。
（1）5月份甲超市的销售额比乙超市多多少？123月份4月份 5月份 甲超市
销售额 乙超市
销售额a a a(1＋x%) a(1＋x%) x(1＋x%)
= a(1＋x%)2 a(1－x%) x(1－x%) = a(1－x%)2 a(1－x%) 差额为： a(1＋x%)2－a(1－x%)2=a(1＋——＋—— )2x100 10000x2解：当a=150，x=2时， =12（万元）（2）如果a=150，x=2，那么5月份甲超市的销售额
比乙超市多多少万元？132、有两个圆，较大圆的半径为r，较小圆的
半径比较大圆的半径小3mm，求两圆的面积差，　
　当r=10mm时，面积之差是多少？
　当r=15mm时呢？ 练一练14例3. 将一张边长为acm的正方形纸板的四角各剪去
一个边长为bcm的小正方形，然后把它折成一个无盖
的纸盒，用a、b的多项式表示纸盒的体积；ab15例题4.的值为零？16思考题已知x+y=3，xy=1，求x2+y2与(x-y)2的值.x2+y2=(x+y) 2-2xy=32-2=7(x-y) 2=(x+y) 2-2xy-2xy=32-4=517能力挑战：　　1、已知 x + y =10，xy=24，
则 x2 + y2 = ;522、已知 x + y =3， x2 + y2 =7，
则 xy = ;118中考链接1. (2012山西中考题，)先化简，再求值．解：192.如图，从边长为（a+4）cm的正方形纸片中剪去一个边长为
（a+1）cm的正方形（a＞0），剩余部分沿虚线又剪拼成一个矩
形（不重叠无缝隙），则矩形的面积为（　　）（2011芜湖市中考题）A、（2a2+5a）cm B、（3a+15）cm
C、（6a+9）cm D、（6a+15）cm2222
D20观察下列各式：
52=25
152=225
252=625
352=1225
……
小组合作,探究推理 2152=25
152=225
252=625
352=1225
452=2025
……
752=5625
852=7225 可写成 ＋25
可写成 ＋25
可写成 ＋25
可写成 ＋25
可写成 ＋25
……
可写成
可写成 100×1×（1＋1）100×2×（2＋1）100×3×（3＋1）100×4×（4＋1）（1）探索规律： 100×0×（0＋1）（2）归纳、猜想 ：
（3）根据上面的归纳、猜想，试计算：
20052= 。100×7×8 ＋25100×8×9 ＋254０20025真厉害！ （10n＋5）2= 100n2+100n+25= 100ｎ(ｎ+１) +2522课堂小结：一、你能说出这节课的收获吗？二、应用整式解决实际问题的基本过程：23§3.5整式的化简2.平方差公式、完全平方公式的运用；
3.利用整式的运算解决简单的实际问题；1.整式的加、减、乘、乘方的运算；一、知识收获二、能力收获1、整式化简的一般顺序：先乘方，再乘除，最后加减；能用
乘法公式的尽量用公式来计算使计算简便.
2、要把握各种公式的特征和运算法则；通过式子的变形和逆
向应用公式，达到灵活运用公式的目的.
3、掌握整体代入法，简化运算过程，进一步体会“转化”的数
学思想；
4、化简的结果要求化到最简，最后结果若含有同类项，则要
合并同类项；245、求代数式的值时，为使计算简便，一般要先化简，再代入求值；通常有以下几种形式：
(1)利用非负数之和为零求值；
(2)利用互为相反数求值；
(3)利用降次求值.
6、完全平方公式中常用的公式变形：
(1)
(2)
(3)
(4)
(5)
(6)
25【1】、复习、整理、巩固今天所学知识。一、必做题：1、作业本(1)第17--18页T1—T7；
2、参书第81页A组题T1—T4；
3.课时特训第49、50页T1—T16；
二、选做题：1、参书第81页B、C组题T5—T7；
2.拓展探究题：参看幻灯片第26--29号。
三、抄写第22--23张幻灯片的内容。【2】、书面作业布置作业：26拓展探究题2.已知-2x+3y=5，求2(2x-3y) +6y-4x-10 的值.
23.已知a=2012x+2011，b=2012x+2012，
C=2012x+2013求a +b +c –ab-bc-ac的值.222274.已知x+y=3，xy=1，
求x2+y2与(x-y)2的值.5.已知 求
的值. 6.已知x2+y2 -4x-6y+13=0,
求x-y的值.287.29同学们，再见！