5.5 分式方程(2) 课件(共20张PPT)
文档属性
| 名称 | 5.5 分式方程(2) 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 984.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-18 16:47:16 | ||
图片预览






文档简介
(共20张PPT)
5.5 分式方程 (2)
基本的数量关系,托底的
基本的相等关系,寻找的
浙教版 七年级下册
江中春水,水位上涨,大船也如轻毛。一向要枉费巨力才能推动,
现在却在水中,自由的飞驰。朱熹在告诉学习者,读书不能用蛮力,
而要巧借力,否则,就会事倍功半。
昨天夜晚江边的春水大涨,那艘庞大的船就像一根羽毛一样轻。
以往花费许多力量也不能推动它,今天在水中间却能自在地移动。
新课引入
观书有感 其二
宋 朱熹
昨夜江边春水生,
艨艟巨舰一毛轻。
向来枉费推移力,
此日中流自在行。
meng chong
温故知新
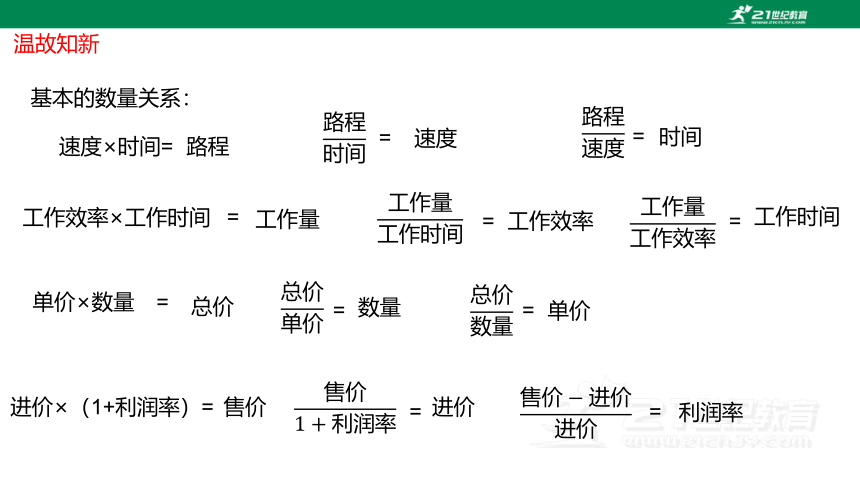
基本的数量关系:
速度×时间=
路程
=
时间
=
速度
工作效率×工作时间
=
工作量
=
工作时间
=
工作效率
单价×数量
=
总价
=
数量
=
单价
进价×(1+利润率)=
售价
进价
=
=
利润率
基本的相等关系:
1.表示同一个量的两个不同式子相等.
2.总量等于各部分量的和.
3.文字表达与等式表达在语序上的对应一致性.
例1. 某地水稻种植基地在A,B两个面积相同的试验田里种植不同品种的 水稻,分别收获16.8吨和13.2吨.已知A试验田的水稻比B试验田的水稻每公顷多收获3吨,分别求A,B两个试验田每公顷的水稻产量.
解: 设A试验田每公顷产量为x吨,则B试验田每公顷产量为(x-3)吨.
经检验,x=14是所列方程的根,且符合题意.
14-3=11(吨).
答:A试验田每公顷产量是14吨,B试验田每公顷产量是11吨.
由题意可得
基本的相等关系:
基本的数量关系:
分析:
A试验田面积=B试验田面积.
=
每块试验田的面积(公顷)
=
16.8(x-3)=13.2x
16.8x-16.8×3=13.2x
3.6x=16.8×3
x=14
甲、乙两人每小时共做35个电器零件。两人同时开始工作,当甲做了90个零件时,乙做了120个。问甲、乙每小时各做多少个电器零件?
解:设甲每小时能做x个电器零件,则乙每小时能做
(35-x)个零件,由题意得
解得 x=15
经检验,x=15是所列方程的根,且符合题意
35-x=35-15=20
答:甲每小时能做15个,乙每小时能做20个.
学以致用
=
工作时间=
分析:
基本的数量关系:
基本的相等关系:
甲工作时间=乙工作时间
关键的,两个基本
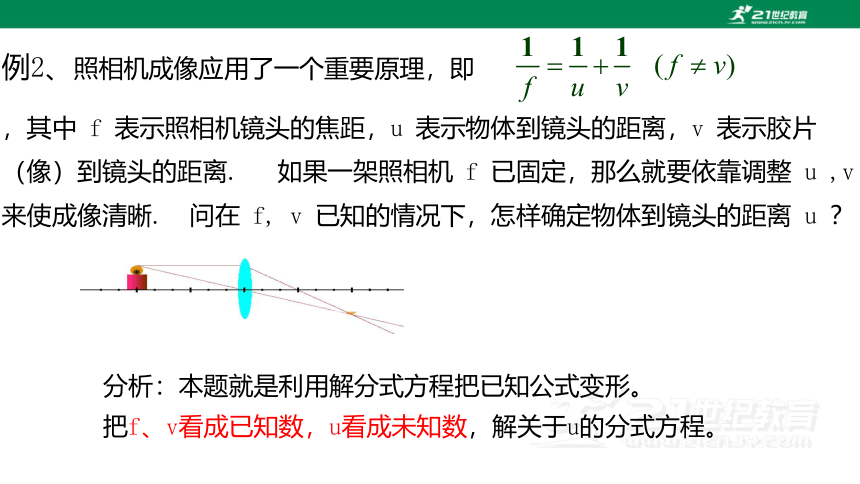
分析:本题就是利用解分式方程把已知公式变形。
把f、v看成已知数,u看成未知数,解关于u的分式方程。
例2、照相机成像应用了一个重要原理,即
,其中 f 表示照相机镜头的焦距,u 表示物体到镜头的距离,v 表示胶片(像)到镜头的距离. 如果一架照相机 f 已固定,那么就要依靠调整 u ,v 来使成像清晰. 问在 f, v 已知的情况下,怎样确定物体到镜头的距离 u ?
解:把f,v均看做已知数,解以u为未知数的方程:
∴当f≠v时,
uv=fv+fu
uv-fu=fv
(v-f)u=fv
(f≠v)
=
+
u=
检验:因为v,f不为零,f≠v,所以 u= 是分式方程 的根.
=
+
答:在已知f,v的情况下,物体到镜头的距离u可以由公式 u = 来确定.
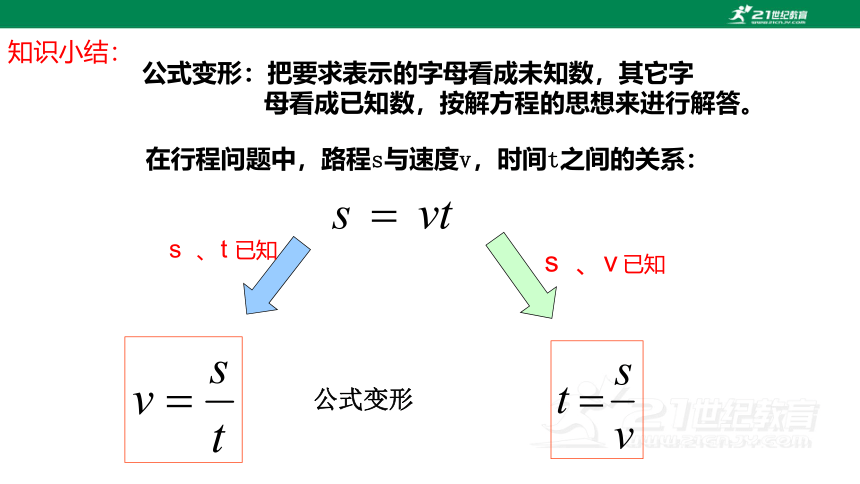
在行程问题中,路程s与速度v,时间t之间的关系:
公式变形
公式变形:把要求表示的字母看成未知数,其它字
母看成已知数,按解方程的思想来进行解答。
知识小结:
s 、t 已知
s 、v 已知
学以致用:
解:
2s=(a+b)h
2s=ah+bh
2s-ah=bh
=b
b=
领悟的,给b 点颜色看看!
列分式方程解应用题的一般步骤
1.审:分析题意,找出等量关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据等量关系,正确列出代数式和方程.
4.解:求出所列方程的解.
5.验:有二次检验.
6.答:注意单位和语言完整.
二次检验是:
(1)是不是所列方程的解;
(2)是否满足实际意义.
知识小结:
1.一家工艺品厂按计件方式结算工资.暑假里,大学生小华去这家工艺品厂打工,第一天得到工资60元,第二天小华比第一天多编了10件,得到工资75元.问小华第一天编了多少件 每件工资是多少
解:设小华第一天编了x件,由题意,得
经检验,x=40是原方程的根,且符合题意.
答:小华第一天编了40件,每件工资是1.5元.
分析:
基本的数量关系:
基本的相等关系:
=
单价
表示同一个量的两个不同式子相等.
夯实基础,稳扎稳打
=
60(x+10)=75x
15x=600
x=40
=1.5
锁定两个基本,艨艟巨舰一毛轻
2.四川5·12特大地震发生后,受灾地区急需大量赈灾帐篷.某帐篷生产企业接到生产任务后,加大生产投入、提高生产效率,实际每天生产帐篷比原计划多200顶.已知现在生产3000顶帐篷所用的时间与原计划生产2000顶的时间相同,问该企业现在每天能生产多少顶帐篷
解:设现在能每天生产x顶,由题意,得
解得x=600.
答:该企业现在每天能生产600顶.
经检验,x=600是原方程的根,且符合题意.
分析:
基本的数量关系:
基本的相等关系:
=
工作时间
表示同一个量的两个不同式子相等.
锁定两个基本,此日中流自在行。
3.某班同学到距学校12千米的烈士陵园扫墓.一部分同学骑自行车先行,经半小时后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是自行车速度的3倍,求自行车和汽车的速度.
解:设自行车的速度为x千米/时,由题意,得
解得x=16.
所以汽车的速度为3×16=48(千米/时).
经检验,x=16是原方程的根,且符合题意.
答:自行车的速度为16千米/时,汽车的速度为48千米/时.
连续递推,豁然开朗
文字表达与等式表达在语序上的对应一致性.
分析:
基本的数量关系:
基本的相等关系:
=
时间
4、 现有甲,乙,丙三种糖果混合而成的什锦糖果50千克,其中各种糖果的千克数和单价如下表:
甲种糖果 乙种糖果 丙种糖果
千克数 10 20 20
单价(元/千克) 25 20 15
商店以糖果的平均价作为什锦糖的单价,若要使什锦糖的单价提高1元/千克,问需加入甲种糖多少千克?
=
单价
分析:
基本的数量关系:
基本的相等关系:
总量等于各部分量的和.
甲种糖果 乙种糖果 丙种糖果
千克数 10 20 20
单价(元/千克) 25 20 15
解;设需加入甲种糖果x千克,可得方程:
x=10
=19(元/千克)
提价后的什锦糖单价:19+1=20 (元/千克)
分析:提价前的什锦糖单价:
经检验,x=10是原方程的根,且符合题意.
答:需加入甲种糖10千克
5. 工厂生产一种电子配件,每只的成本为2元,毛利率为25%;后来该工厂通过改进工艺,降低了成本,在售价不变的情况下,毛利率增加了15%.问这种配件每只的成本降低了多少元?(精确到0.01元)
解:设这种配件每只的成本降低了x元.根据题意得:
解这个方程,得
2.5-(2-x)
2-x
=
25%+15%
x=
14
3
≈0.21
答:每只成本降低了0.21元
思维拓展,更上一层
经检验,x= 是原方程的根,且符合题意.
基本的相等关系:
基本的数量关系:
分析:
=
利润率
表示同一个量的两个不同式子相等
课堂小结
实际问题
找等量关系
设未知数、列方程
数学问题
(分式方程)
解方程
方程的解
检验
实际问题
的答案
建模
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
5.5 分式方程 (2)
基本的数量关系,托底的
基本的相等关系,寻找的
浙教版 七年级下册
江中春水,水位上涨,大船也如轻毛。一向要枉费巨力才能推动,
现在却在水中,自由的飞驰。朱熹在告诉学习者,读书不能用蛮力,
而要巧借力,否则,就会事倍功半。
昨天夜晚江边的春水大涨,那艘庞大的船就像一根羽毛一样轻。
以往花费许多力量也不能推动它,今天在水中间却能自在地移动。
新课引入
观书有感 其二
宋 朱熹
昨夜江边春水生,
艨艟巨舰一毛轻。
向来枉费推移力,
此日中流自在行。
meng chong
温故知新
基本的数量关系:
速度×时间=
路程
=
时间
=
速度
工作效率×工作时间
=
工作量
=
工作时间
=
工作效率
单价×数量
=
总价
=
数量
=
单价
进价×(1+利润率)=
售价
进价
=
=
利润率
基本的相等关系:
1.表示同一个量的两个不同式子相等.
2.总量等于各部分量的和.
3.文字表达与等式表达在语序上的对应一致性.
例1. 某地水稻种植基地在A,B两个面积相同的试验田里种植不同品种的 水稻,分别收获16.8吨和13.2吨.已知A试验田的水稻比B试验田的水稻每公顷多收获3吨,分别求A,B两个试验田每公顷的水稻产量.
解: 设A试验田每公顷产量为x吨,则B试验田每公顷产量为(x-3)吨.
经检验,x=14是所列方程的根,且符合题意.
14-3=11(吨).
答:A试验田每公顷产量是14吨,B试验田每公顷产量是11吨.
由题意可得
基本的相等关系:
基本的数量关系:
分析:
A试验田面积=B试验田面积.
=
每块试验田的面积(公顷)
=
16.8(x-3)=13.2x
16.8x-16.8×3=13.2x
3.6x=16.8×3
x=14
甲、乙两人每小时共做35个电器零件。两人同时开始工作,当甲做了90个零件时,乙做了120个。问甲、乙每小时各做多少个电器零件?
解:设甲每小时能做x个电器零件,则乙每小时能做
(35-x)个零件,由题意得
解得 x=15
经检验,x=15是所列方程的根,且符合题意
35-x=35-15=20
答:甲每小时能做15个,乙每小时能做20个.
学以致用
=
工作时间=
分析:
基本的数量关系:
基本的相等关系:
甲工作时间=乙工作时间
关键的,两个基本
分析:本题就是利用解分式方程把已知公式变形。
把f、v看成已知数,u看成未知数,解关于u的分式方程。
例2、照相机成像应用了一个重要原理,即
,其中 f 表示照相机镜头的焦距,u 表示物体到镜头的距离,v 表示胶片(像)到镜头的距离. 如果一架照相机 f 已固定,那么就要依靠调整 u ,v 来使成像清晰. 问在 f, v 已知的情况下,怎样确定物体到镜头的距离 u ?
解:把f,v均看做已知数,解以u为未知数的方程:
∴当f≠v时,
uv=fv+fu
uv-fu=fv
(v-f)u=fv
(f≠v)
=
+
u=
检验:因为v,f不为零,f≠v,所以 u= 是分式方程 的根.
=
+
答:在已知f,v的情况下,物体到镜头的距离u可以由公式 u = 来确定.
在行程问题中,路程s与速度v,时间t之间的关系:
公式变形
公式变形:把要求表示的字母看成未知数,其它字
母看成已知数,按解方程的思想来进行解答。
知识小结:
s 、t 已知
s 、v 已知
学以致用:
解:
2s=(a+b)h
2s=ah+bh
2s-ah=bh
=b
b=
领悟的,给b 点颜色看看!
列分式方程解应用题的一般步骤
1.审:分析题意,找出等量关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据等量关系,正确列出代数式和方程.
4.解:求出所列方程的解.
5.验:有二次检验.
6.答:注意单位和语言完整.
二次检验是:
(1)是不是所列方程的解;
(2)是否满足实际意义.
知识小结:
1.一家工艺品厂按计件方式结算工资.暑假里,大学生小华去这家工艺品厂打工,第一天得到工资60元,第二天小华比第一天多编了10件,得到工资75元.问小华第一天编了多少件 每件工资是多少
解:设小华第一天编了x件,由题意,得
经检验,x=40是原方程的根,且符合题意.
答:小华第一天编了40件,每件工资是1.5元.
分析:
基本的数量关系:
基本的相等关系:
=
单价
表示同一个量的两个不同式子相等.
夯实基础,稳扎稳打
=
60(x+10)=75x
15x=600
x=40
=1.5
锁定两个基本,艨艟巨舰一毛轻
2.四川5·12特大地震发生后,受灾地区急需大量赈灾帐篷.某帐篷生产企业接到生产任务后,加大生产投入、提高生产效率,实际每天生产帐篷比原计划多200顶.已知现在生产3000顶帐篷所用的时间与原计划生产2000顶的时间相同,问该企业现在每天能生产多少顶帐篷
解:设现在能每天生产x顶,由题意,得
解得x=600.
答:该企业现在每天能生产600顶.
经检验,x=600是原方程的根,且符合题意.
分析:
基本的数量关系:
基本的相等关系:
=
工作时间
表示同一个量的两个不同式子相等.
锁定两个基本,此日中流自在行。
3.某班同学到距学校12千米的烈士陵园扫墓.一部分同学骑自行车先行,经半小时后,其余同学乘汽车出发,结果他们同时到达.已知汽车的速度是自行车速度的3倍,求自行车和汽车的速度.
解:设自行车的速度为x千米/时,由题意,得
解得x=16.
所以汽车的速度为3×16=48(千米/时).
经检验,x=16是原方程的根,且符合题意.
答:自行车的速度为16千米/时,汽车的速度为48千米/时.
连续递推,豁然开朗
文字表达与等式表达在语序上的对应一致性.
分析:
基本的数量关系:
基本的相等关系:
=
时间
4、 现有甲,乙,丙三种糖果混合而成的什锦糖果50千克,其中各种糖果的千克数和单价如下表:
甲种糖果 乙种糖果 丙种糖果
千克数 10 20 20
单价(元/千克) 25 20 15
商店以糖果的平均价作为什锦糖的单价,若要使什锦糖的单价提高1元/千克,问需加入甲种糖多少千克?
=
单价
分析:
基本的数量关系:
基本的相等关系:
总量等于各部分量的和.
甲种糖果 乙种糖果 丙种糖果
千克数 10 20 20
单价(元/千克) 25 20 15
解;设需加入甲种糖果x千克,可得方程:
x=10
=19(元/千克)
提价后的什锦糖单价:19+1=20 (元/千克)
分析:提价前的什锦糖单价:
经检验,x=10是原方程的根,且符合题意.
答:需加入甲种糖10千克
5. 工厂生产一种电子配件,每只的成本为2元,毛利率为25%;后来该工厂通过改进工艺,降低了成本,在售价不变的情况下,毛利率增加了15%.问这种配件每只的成本降低了多少元?(精确到0.01元)
解:设这种配件每只的成本降低了x元.根据题意得:
解这个方程,得
2.5-(2-x)
2-x
=
25%+15%
x=
14
3
≈0.21
答:每只成本降低了0.21元
思维拓展,更上一层
经检验,x= 是原方程的根,且符合题意.
基本的相等关系:
基本的数量关系:
分析:
=
利润率
表示同一个量的两个不同式子相等
课堂小结
实际问题
找等量关系
设未知数、列方程
数学问题
(分式方程)
解方程
方程的解
检验
实际问题
的答案
建模
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
