5.5 分式方程(1) 课件(共20张PPT)
文档属性
| 名称 | 5.5 分式方程(1) 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 13:06:53 | ||
图片预览







文档简介
(共20张PPT)
5.5分式方程(1)
浙教版 七年级下
回顾导入
整式方程:
方程两边都是整式的方程.
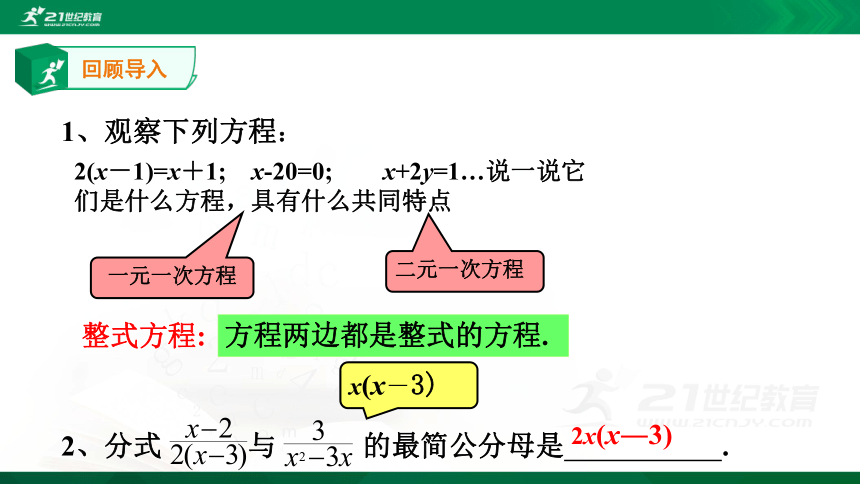
1、观察下列方程:
一元一次方程
二元一次方程
2(x-1)=x+1; x-20=0; x+2y=1…说一说它们是什么方程,具有什么共同特点
x(x―3)
2x(x―3)
2、分式 与 的最简公分母是 .
合作探究
最近,我市联通分公司调低了长途电话的话费标准,每分钟费用降低了25%,据营业员介绍,按原收费标准6元花费的通话时间,在新收费标准下可多通话5分钟,请帮老师计算一下,前后两种收费标准每分钟收费各是多少?
在上面的问题中,主要等量关系是什么
6元话费 按原收费标准的通话时间+5
= 按新收费标准的通话时间
=
+5
如果设原来的收费标准是 元/分,可列怎样的方程
长话费调 低了
思考:该方程与我们刚才复习的整式方程有什么不同
新知归纳
类比整式方程,你能说一说上述方程是什么方程吗?
分式方程的定义:
只含分式,或分式和整式,并且分母时含有未知数
的方程叫做分式方程。
归纳:
教材做一做
判断下列方程是不是分式方程?为什么?
答案:分式方程(2)(3),
(1)(4)的是一元一次方程,因为分母没有字母
例题讲解
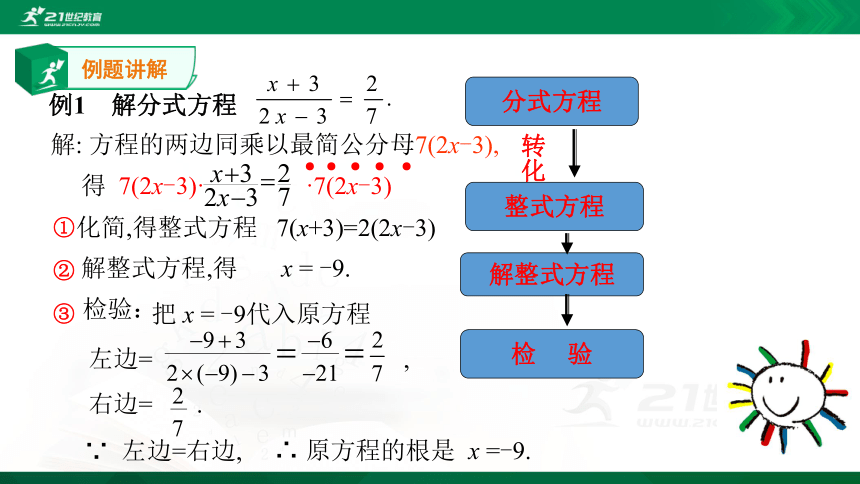
得 7(2x-3)· ·7(2x-3)
例1 解分式方程
化简,得整式方程 7(x+3)=2(2x-3)
解整式方程,得 x = -9.
把 x = -9代入原方程
左边= ,
右边= .
∵ 左边=右边,
∴ 原方程的根是 x =-9.
● ● ● ● ●
分式方程
整式方程
解整式方程
检 验
转化
① ② ③
检验:
解: 方程的两边同乘以最简公分母7(2x-3),
例题讲解
例2 解方程
解 方程两边同乘以最简公分母(x-3),
解整式方程,得 x = 3
检验:把x = 3 代入原方程
结果使原方程的最简公分母x-3=0 ,分式无意义,因此x = 3不是原方程的根.
∴ 原方程无解 .
① ② ③
得 2-x=-1-2(x-3).
增根
新知归纳
⑵ 找出各分母的最简公分母;
⑶ 方程两边各项乘以最简公分母;
⑴ 把各分母分解因式;
解分式方程的步骤:
去分母,化为整式方程:
解整式方程。
把未知数的值代入原方程,
看左右两边的值是否相等。
检验:
疑问:检验必须是书面检验吗?
教材同步练习
新知归纳
解分式方程容易犯的错误主要有:
(1)去分母时,原方程的整式部分漏乘.
(2)约去分母后,分子是多项式时, 要注意添括号.
(3)增根不舍掉.
(4)……
新知归纳
增根的定义
增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.
产生的原因:分式方程两边同乘以一个零因式后,所得的根是整式方程的根,而不是分式方程的根.
····
····
使分母为零的根
······
···
必须检验
例题讲解
解:∵原分式方程有增根,∴x(x-1)=0.
解得x=0或x=1.
∵x=0不可能是整式方程(a+2)x=3的根,
∴原分式方程的增根为x=1.∴(a+2)×1=3.解得a=1.
解:去分母并整理,得(a+2)x=3.
因为x=1是原方程的增根,所以(a+2)×1=3.解得a=1.
(1)若方程的增根为x=1,求a的值;
(2)若方程有增根,求a的值;
例题讲解
3
解:①当a+2=0时,整式方程(a+2)x=3无解.
此时a=-2.
②当a+2≠0时,要使原方程无解,则x(x-1)=0.解得x=0或x=1.把x=0代入整式方程,a的值不存在;把x=1代入整式方程,得a=1.
综合①②得a的值为-2或1.
(3)若方程无解,求a的值.
当堂小结
你有什么收获吗
要注意灵活运用解分式方程的步骤
解分式方程 容易发生的错误
分式方程的 概念.
解分式方程的 一般步骤 .
解分式方程的 主要思想.
拓展提高
A
D
拓展提高
C
A
拓展提高
拓展提高
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
5.5分式方程(1)
浙教版 七年级下
回顾导入
整式方程:
方程两边都是整式的方程.
1、观察下列方程:
一元一次方程
二元一次方程
2(x-1)=x+1; x-20=0; x+2y=1…说一说它们是什么方程,具有什么共同特点
x(x―3)
2x(x―3)
2、分式 与 的最简公分母是 .
合作探究
最近,我市联通分公司调低了长途电话的话费标准,每分钟费用降低了25%,据营业员介绍,按原收费标准6元花费的通话时间,在新收费标准下可多通话5分钟,请帮老师计算一下,前后两种收费标准每分钟收费各是多少?
在上面的问题中,主要等量关系是什么
6元话费 按原收费标准的通话时间+5
= 按新收费标准的通话时间
=
+5
如果设原来的收费标准是 元/分,可列怎样的方程
长话费调 低了
思考:该方程与我们刚才复习的整式方程有什么不同
新知归纳
类比整式方程,你能说一说上述方程是什么方程吗?
分式方程的定义:
只含分式,或分式和整式,并且分母时含有未知数
的方程叫做分式方程。
归纳:
教材做一做
判断下列方程是不是分式方程?为什么?
答案:分式方程(2)(3),
(1)(4)的是一元一次方程,因为分母没有字母
例题讲解
得 7(2x-3)· ·7(2x-3)
例1 解分式方程
化简,得整式方程 7(x+3)=2(2x-3)
解整式方程,得 x = -9.
把 x = -9代入原方程
左边= ,
右边= .
∵ 左边=右边,
∴ 原方程的根是 x =-9.
● ● ● ● ●
分式方程
整式方程
解整式方程
检 验
转化
① ② ③
检验:
解: 方程的两边同乘以最简公分母7(2x-3),
例题讲解
例2 解方程
解 方程两边同乘以最简公分母(x-3),
解整式方程,得 x = 3
检验:把x = 3 代入原方程
结果使原方程的最简公分母x-3=0 ,分式无意义,因此x = 3不是原方程的根.
∴ 原方程无解 .
① ② ③
得 2-x=-1-2(x-3).
增根
新知归纳
⑵ 找出各分母的最简公分母;
⑶ 方程两边各项乘以最简公分母;
⑴ 把各分母分解因式;
解分式方程的步骤:
去分母,化为整式方程:
解整式方程。
把未知数的值代入原方程,
看左右两边的值是否相等。
检验:
疑问:检验必须是书面检验吗?
教材同步练习
新知归纳
解分式方程容易犯的错误主要有:
(1)去分母时,原方程的整式部分漏乘.
(2)约去分母后,分子是多项式时, 要注意添括号.
(3)增根不舍掉.
(4)……
新知归纳
增根的定义
增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.
产生的原因:分式方程两边同乘以一个零因式后,所得的根是整式方程的根,而不是分式方程的根.
····
····
使分母为零的根
······
···
必须检验
例题讲解
解:∵原分式方程有增根,∴x(x-1)=0.
解得x=0或x=1.
∵x=0不可能是整式方程(a+2)x=3的根,
∴原分式方程的增根为x=1.∴(a+2)×1=3.解得a=1.
解:去分母并整理,得(a+2)x=3.
因为x=1是原方程的增根,所以(a+2)×1=3.解得a=1.
(1)若方程的增根为x=1,求a的值;
(2)若方程有增根,求a的值;
例题讲解
3
解:①当a+2=0时,整式方程(a+2)x=3无解.
此时a=-2.
②当a+2≠0时,要使原方程无解,则x(x-1)=0.解得x=0或x=1.把x=0代入整式方程,a的值不存在;把x=1代入整式方程,得a=1.
综合①②得a的值为-2或1.
(3)若方程无解,求a的值.
当堂小结
你有什么收获吗
要注意灵活运用解分式方程的步骤
解分式方程 容易发生的错误
分式方程的 概念.
解分式方程的 一般步骤 .
解分式方程的 主要思想.
拓展提高
A
D
拓展提高
C
A
拓展提高
拓展提高
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
