浙教版七年级下册 6.5频数直方图 同步练习(含答案)
文档属性
| 名称 | 浙教版七年级下册 6.5频数直方图 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 942.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-29 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版七年级下 6.5频数直方图同步练习
一.选择题
1.(2021秋 金水区校级期末)某学校在植树节派出50名学生参与植树,统计每个人植树的棵数之后,绘制出如图所示的频数分布直方图(图中分组含最小值,不含最大值),则植树不足7棵的人数占总人数的( )
A.40% B.64% C.24% D.96%
2.(2021秋 兴庆区期末)某养羊场对200只羊质量进行统计,得到频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在77.5kg及以上的生羊的只数是( )
A.180 B.140 C.120 D.110
3.(2021秋 武侯区期末)2021年“世界水日”的主题为“珍惜水、爱护水”.小明家安装节水龙头后,他记录了50天的日用水量数据(单位:m3),得到频数分布表如表:
日用水量x 0≤x<0.1 0.1≤x<0.2 0.2≤x<0.3 0.3≤x<0.4 0.4≤x<0.5 0.5≤x<0.6
频数 2 3 5 20 15 5
在记录的这50天中,日用水量小于0.4m3的频率为( )
A.0.9 B.0.6 C.0.3 D.0.2
4.(2021秋 礼泉县期末)某校九年级随机抽查一部分学生进行了1分钟仰卧起坐次数的测试,并将其绘制成如图所示的频数分布直方图.那么仰卧起坐次数在25~30次的人数占抽查总人数的百分比是( )
A.40% B.30% C.20% D.10%
5.(2022 金华模拟)如图,是九(1)班45名同学每周课外阅读时间的频数分布直方图(每组含前一个边界值,不含后一个边界值),由图可知,每周课外阅读时间不小于6小时的人数是( )
A.6人 B.8人 C.14人 D.36人
6.(2022春 正定县期中)某校为了了解学生在校午餐所需的时间,抽量了20名学生在校午餐所需时间,获得如下的数据(单位:分):10、12、15、10、16、18、19、18、20、18、18、20、28、22、30、20、15、16、21、16.若将这些数据以4分为组距进行分组,则组数是( )
A.4组 B.5组 C.6组 D.7组
7.(2021春 荣县校级期中)在频数分布直方图中,用来表示各组频数的是每个矩形的( )
A.长 B.宽(高) C.周长 D.面积
8.(2021 孝义市三模)根据我国国民倾向的阅读形式的调查研究发现,36.7%的成年国民倾向于“拿一本纸质图书阅读”,有43.5%的国民倾向于“手机阅读”,有10.6%的国民更倾向于“网络在线阅读”,有7.8%的人倾向于“在电子阅读器上阅读”,有1.4%的国民“习惯从网上下载并打印下来阅读”.以上数据最适合用下列哪种统计图描述( )
A.条形统计图 B.折线图
C.频数分布直方图 D.扇形统计图
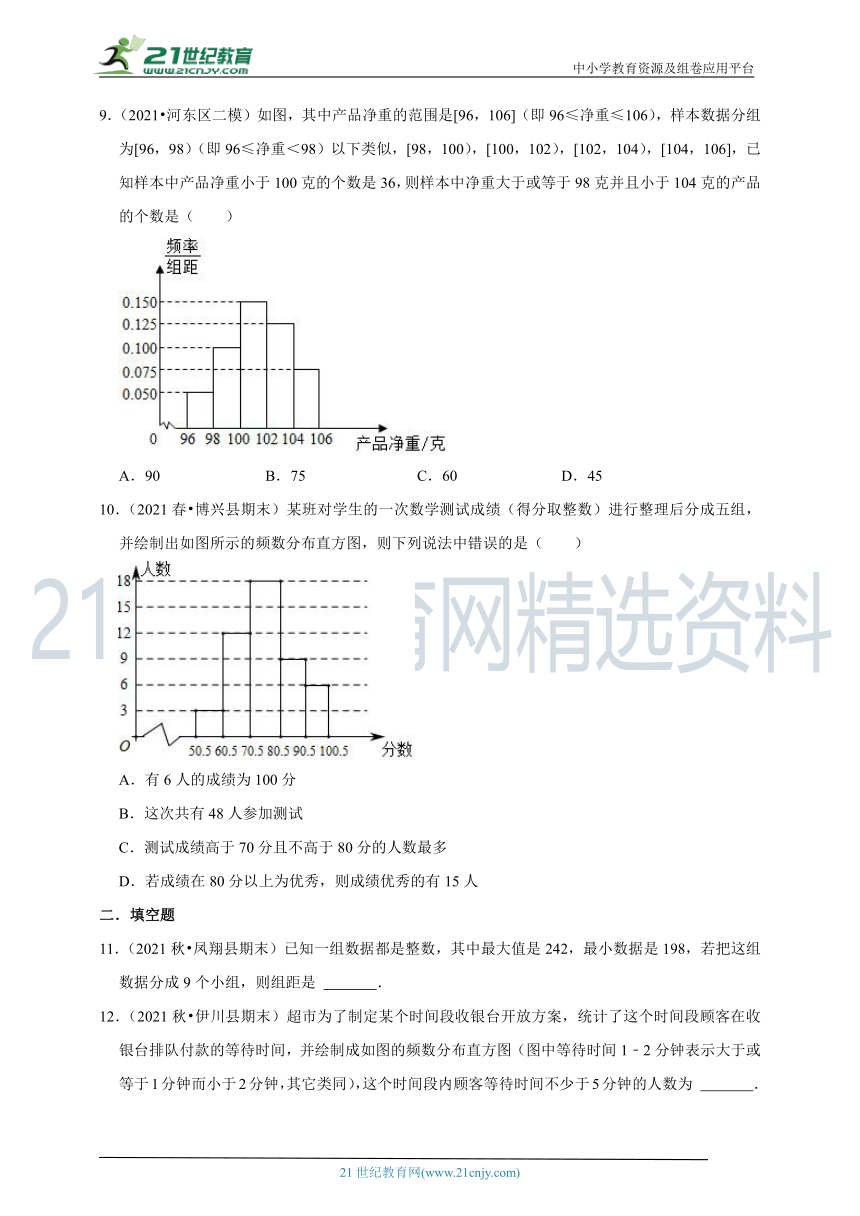
9.(2021 河东区二模)如图,其中产品净重的范围是[96,106](即96≤净重≤106),样本数据分组为[96,98)(即96≤净重<98)以下类似,[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
A.90 B.75 C.60 D.45
10.(2021春 博兴县期末)某班对学生的一次数学测试成绩(得分取整数)进行整理后分成五组,并绘制出如图所示的频数分布直方图,则下列说法中错误的是( )
A.有6人的成绩为100分
B.这次共有48人参加测试
C.测试成绩高于70分且不高于80分的人数最多
D.若成绩在80分以上为优秀,则成绩优秀的有15人
二.填空题
11.(2021秋 凤翔县期末)已知一组数据都是整数,其中最大值是242,最小数据是198,若把这组数据分成9个小组,则组距是 .
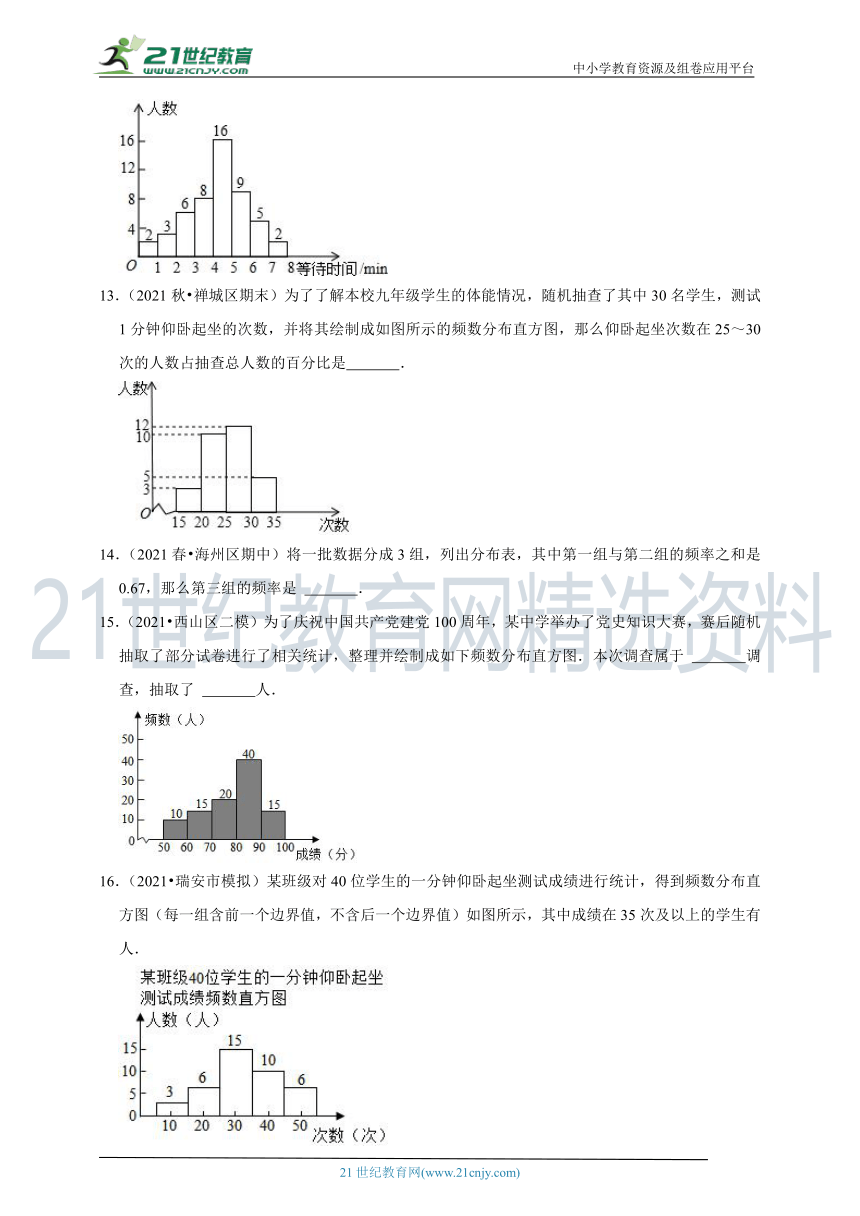
12.(2021秋 伊川县期末)超市为了制定某个时间段收银台开放方案,统计了这个时间段顾客在收银台排队付款的等待时间,并绘制成如图的频数分布直方图(图中等待时间1﹣2分钟表示大于或等于1分钟而小于2分钟,其它类同),这个时间段内顾客等待时间不少于5分钟的人数为 .
13.(2021秋 禅城区期末)为了了解本校九年级学生的体能情况,随机抽查了其中30名学生,测试1分钟仰卧起坐的次数,并将其绘制成如图所示的频数分布直方图,那么仰卧起坐次数在25~30次的人数占抽查总人数的百分比是 .
14.(2021春 海州区期中)将一批数据分成3组,列出分布表,其中第一组与第二组的频率之和是0.67,那么第三组的频率是 .
15.(2021 西山区二模)为了庆祝中国共产党建党100周年,某中学举办了党史知识大赛,赛后随机抽取了部分试卷进行了相关统计,整理并绘制成如下频数分布直方图.本次调查属于 调查,抽取了 人.
16.(2021 瑞安市模拟)某班级对40位学生的一分钟仰卧起坐测试成绩进行统计,得到频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩在35次及以上的学生有 人.
三.解答题
17.(2021秋 河源期末)某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图:
根据图中提供的信息,解答下列问题:
(1)m= ,E组对应的圆心角度数为 °;
(2)补全频数分布直方图.
18.(2022春 泾阳县月考)某校为了提高学生学习国学的积极性,举办了首届“国学知识大赛”,该校所有学生均参加初赛.初赛中,将国学相关知识设置为100分试卷,学生的分数均为50分以上,为了解学生对国学的掌握情况,学校抽取了一部分学生成绩,绘制出不完整的表格和频数分布直方图.
成绩x(分) 频数(人数) 百分比
50<x≤60 2 4%
60<x≤70 10 b
70<x≤80 14 28%
80<x≤90 a 32%
90<x≤100 8 16%
请根据表格提供的信息,解答以下问题:
(1)学校共抽取了 名学生;
(2)求出a、b的值,并补全频数分布直方图;
(3)若将调查结果绘制成扇形统计图,求成绩在“60<x≤70”所对应的扇形圆心角的度数.
19.(2021秋 秦都区期末)某市七年级有3000名学生参加网上“爱我中华知识竞赛”活动,为了解本次知识竞赛成绩的分布情况,从中抽取了200名学生的得分进行统计.
成绩x(分) 频数 频率
50≤x<60 10 a
60≤x<70 16 8%
70≤x<80 b 20%
80≤x<90 62 c
90≤x<100 72 36%
请根据不完整的表格,解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)补全如图所示的频数分布直方图;
(3)若将得分转化为等级,规定50≤x<60评为“D”,60≤x<70评为“C”,70≤x<90评为“B”,90≤x<100评为“A”,并按等级“A”、“B”、“C”、“D”将这次调查的结果绘制成扇形统计图,求等级为“B”的扇形所对应的圆心角度数.
20.(2021秋 宁德期末)为了提升学生的交通安全意识,学校计划开展全员“交通法规”知识竞赛,七(3)班班主任赵老师给全班同学定下的目标是:合格率达90%,优秀率达25%(x<60为不合格;x≥60为合格;x≥90为优秀),为了解班上学生对“交通法规”知识的认知情况,赵老师组织了一次模拟测试,将全班同学的测试成绩整理后作出如下频数分布直方图.(图中的70~80表示70≤x<80,其余类推)
(1)七(3)班共有多少名学生?
(2)赵老师对本次模拟测试结果不满意,请通过计算给出一条她不满意的理由;
(3)模拟测试后,通过强化教育,班级在学校“交通法规”竞赛中成绩有了较大提高,结果优秀人数占合格人数的,比不合格人数多10人.本次竞赛结果是否完成了赵老师预设的目标?请说明理由.
21.(2021秋 中原区校级期末)4月23日是“世界读书日”,我校校团委发起了“让阅读成为习惯”的读书活动,鼓励学生利用周末积极阅读课外书籍.为了解学生周末两天的读书时间,校团委随机调查了部分学生的读书时间x(单位:分钟),把读书时间分为四组:A(30≤x<60),B(60≤x<90),C(90≤x<120),D(120≤x<150).部分数据信息如下:
a.B组和C组的所有数据:85 90 60 70 110 75 65 78 100 90 80 95 90
b.根据调查结果绘制了如下尚不完整的统计图:
请根据以上信息,回答下列问题:
(1)被调查的学生共有 人,并补全频数分布直方图;
(2)在扇形统计图中,C组所对应的扇形圆心角是 ;
(3)请结合统计图给全校学生发出一条合理化的倡议.
答案与解析
一.选择题
1.(2021秋 金水区校级期末)某学校在植树节派出50名学生参与植树,统计每个人植树的棵数之后,绘制出如图所示的频数分布直方图(图中分组含最小值,不含最大值),则植树不足7棵的人数占总人数的( )
A.40% B.64% C.24% D.96%
【解析】解:由图形知,植树不足7棵的人数占总人数的百分比为×100%=24%,
故选:C.
2.(2021秋 兴庆区期末)某养羊场对200只羊质量进行统计,得到频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在77.5kg及以上的生羊的只数是( )
A.180 B.140 C.120 D.110
【解析】解:90+30+20=140(只),
故选:B.
3.(2021秋 武侯区期末)2021年“世界水日”的主题为“珍惜水、爱护水”.小明家安装节水龙头后,他记录了50天的日用水量数据(单位:m3),得到频数分布表如表:
日用水量x 0≤x<0.1 0.1≤x<0.2 0.2≤x<0.3 0.3≤x<0.4 0.4≤x<0.5 0.5≤x<0.6
频数 2 3 5 20 15 5
在记录的这50天中,日用水量小于0.4m3的频率为( )
A.0.9 B.0.6 C.0.3 D.0.2
【解析】解:由表可知,使用后,50天日用水量少于0.4的频数为2+3+5+20=30,
所以估计50天日用水量少于0.4的概率为=0.6.
故选:B.
4.(2021秋 礼泉县期末)某校九年级随机抽查一部分学生进行了1分钟仰卧起坐次数的测试,并将其绘制成如图所示的频数分布直方图.那么仰卧起坐次数在25~30次的人数占抽查总人数的百分比是( )
A.40% B.30% C.20% D.10%
【解析】解:仰卧起坐次数在25~30次的人数占抽查总人数的百分比是×100%=40%,
故选:A.
5.(2022 金华模拟)如图,是九(1)班45名同学每周课外阅读时间的频数分布直方图(每组含前一个边界值,不含后一个边界值),由图可知,每周课外阅读时间不小于6小时的人数是( )
A.6人 B.8人 C.14人 D.36人
【解析】解:由频数分布直方图知,每周课外阅读时间不小于6小时的人数是8+6=14(人),
故选:C.
6.(2022春 正定县期中)某校为了了解学生在校午餐所需的时间,抽量了20名学生在校午餐所需时间,获得如下的数据(单位:分):10、12、15、10、16、18、19、18、20、18、18、20、28、22、30、20、15、16、21、16.若将这些数据以4分为组距进行分组,则组数是( )
A.4组 B.5组 C.6组 D.7组
【解析】解:根据组数=(最大值﹣最小值)÷组距(小数部分要进位),
则(30﹣10)÷4=5,
所以组数为5+1=6.
故选:C.
7.(2021春 荣县校级期中)在频数分布直方图中,用来表示各组频数的是每个矩形的( )
A.长 B.宽(高) C.周长 D.面积
【解析】解:在频数分布直方图中,用来表示各组频数的是每个矩形的面积.
故选:D.
8.(2021 孝义市三模)根据我国国民倾向的阅读形式的调查研究发现,36.7%的成年国民倾向于“拿一本纸质图书阅读”,有43.5%的国民倾向于“手机阅读”,有10.6%的国民更倾向于“网络在线阅读”,有7.8%的人倾向于“在电子阅读器上阅读”,有1.4%的国民“习惯从网上下载并打印下来阅读”.以上数据最适合用下列哪种统计图描述( )
A.条形统计图 B.折线图
C.频数分布直方图 D.扇形统计图
【解析】解:由题意,用扇形统计图,可以描述国民阅读形式的百分比.
故选:D.
9.(2021 河东区二模)如图,其中产品净重的范围是[96,106](即96≤净重≤106),样本数据分组为[96,98)(即96≤净重<98)以下类似,[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
A.90 B.75 C.60 D.45
【解析】解:∵样本中产品净重小于100克的个数是36,其对应频率之和为:0.05×2+0.1×2=0.3,
∴样本总数为:36÷0.3=120,
∴样本中净重大于或等于98克并且小于104克的产品的个数是:120×(0.1×2+0.15×2+0.125×2)=90.
故选:A.
10.(2021春 博兴县期末)某班对学生的一次数学测试成绩(得分取整数)进行整理后分成五组,并绘制出如图所示的频数分布直方图,则下列说法中错误的是( )
A.有6人的成绩为100分
B.这次共有48人参加测试
C.测试成绩高于70分且不高于80分的人数最多
D.若成绩在80分以上为优秀,则成绩优秀的有15人
【解析】解:A、由图可知90.5~100.5组的有6人,不一定都是100分,此选项错误;
B、这次活动共抽调了3+12+18+9+6=48人测试,此选项正确;
C、测试成绩在70﹣80分的人数为18人,最多,此选项正确;
D、测试成绩在80分以上的人数为15人,此选项正确;
故选:A.
二.填空题
11.(2021秋 凤翔县期末)已知一组数据都是整数,其中最大值是242,最小数据是198,若把这组数据分成9个小组,则组距是 5 .
【解析】解:这组数据的极差为242﹣198=44,
44÷9≈4.9,
所以组距为5,
故答案为:5.
12.(2021秋 伊川县期末)超市为了制定某个时间段收银台开放方案,统计了这个时间段顾客在收银台排队付款的等待时间,并绘制成如图的频数分布直方图(图中等待时间1﹣2分钟表示大于或等于1分钟而小于2分钟,其它类同),这个时间段内顾客等待时间不少于5分钟的人数为 16 .
【解析】解:由直方图可得,
这个时间段内顾客等待时间不少于5分钟的人数为:9+5+2=16,
故答案为:16.
13.(2021秋 禅城区期末)为了了解本校九年级学生的体能情况,随机抽查了其中30名学生,测试1分钟仰卧起坐的次数,并将其绘制成如图所示的频数分布直方图,那么仰卧起坐次数在25~30次的人数占抽查总人数的百分比是 40% .
【解析】解:×100%=40%,
即仰卧起坐次数在25~30次的人数占抽查总人数的百分比是40%,
故答案为:40%.
14.(2021春 海州区期中)将一批数据分成3组,列出分布表,其中第一组与第二组的频率之和是0.67,那么第三组的频率是 0.33 .
【解析】解:第三组的频率是:1﹣0.67=0.33;
故答案为:0.33.
15.(2021 西山区二模)为了庆祝中国共产党建党100周年,某中学举办了党史知识大赛,赛后随机抽取了部分试卷进行了相关统计,整理并绘制成如下频数分布直方图.本次调查属于 抽样调查 调查,抽取了 100 人.
【解析】解:为了庆祝中国共产党建党100周年,某中学举办了党史知识大赛,赛后随机抽取了部分试卷进行了相关统计,整理并绘制成如下频数分布直方图.
本次调查属于抽样调查,抽取了:10+15+20+40+15=100(人).
故答案为:抽样调查;100.
16.(2021 瑞安市模拟)某班级对40位学生的一分钟仰卧起坐测试成绩进行统计,得到频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩在35次及以上的学生有 16 人.
【解析】解:由直方图可得,
成绩为在35次及以上的学生有:10+6=16(人),
故答案为:16.
三.解答题
17.(2021秋 河源期末)某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图:
根据图中提供的信息,解答下列问题:
(1)m= 40 ,E组对应的圆心角度数为 14.4 °;
(2)补全频数分布直方图.
【解析】解:(1)本次调查的人数为:10÷10%=100,
m%=40÷100×100%=40%,
∴m=40,
E组对应的圆心角度数为:(1﹣21%﹣40%﹣25%﹣10%)×360°=14.4°,
故答案为:40,14.4;
(2)D组的频数为:100×25%=25,
补全的频数分布直方图如图所示;
.
18.(2022春 泾阳县月考)某校为了提高学生学习国学的积极性,举办了首届“国学知识大赛”,该校所有学生均参加初赛.初赛中,将国学相关知识设置为100分试卷,学生的分数均为50分以上,为了解学生对国学的掌握情况,学校抽取了一部分学生成绩,绘制出不完整的表格和频数分布直方图.
成绩x(分) 频数(人数) 百分比
50<x≤60 2 4%
60<x≤70 10 b
70<x≤80 14 28%
80<x≤90 a 32%
90<x≤100 8 16%
请根据表格提供的信息,解答以下问题:
(1)学校共抽取了 50 名学生;
(2)求出a、b的值,并补全频数分布直方图;
(3)若将调查结果绘制成扇形统计图,求成绩在“60<x≤70”所对应的扇形圆心角的度数.
【解析】解:(1)由表格可得,
本次决赛的学生数为:10÷0.2=50,
故答案为:50;
(2)a=50×0.32=16,b=10÷50=20%,
补全的频数分布直方图如右图所示,
(3)360°×20%=72°,
故成绩在“60<x≤70”所对应的扇形圆心角的度数为72°.
19.(2021秋 秦都区期末)某市七年级有3000名学生参加网上“爱我中华知识竞赛”活动,为了解本次知识竞赛成绩的分布情况,从中抽取了200名学生的得分进行统计.
成绩x(分) 频数 频率
50≤x<60 10 a
60≤x<70 16 8%
70≤x<80 b 20%
80≤x<90 62 c
90≤x<100 72 36%
请根据不完整的表格,解答下列问题:
(1)填空:a= 5% ,b= 40 ,c= 31% ;
(2)补全如图所示的频数分布直方图;
(3)若将得分转化为等级,规定50≤x<60评为“D”,60≤x<70评为“C”,70≤x<90评为“B”,90≤x<100评为“A”,并按等级“A”、“B”、“C”、“D”将这次调查的结果绘制成扇形统计图,求等级为“B”的扇形所对应的圆心角度数.
【解析】解:(1)调查总人数为16÷8%=200(人),
∴a=10÷200×100%=5%,b=200×20%=40(人),c=62÷200×100%=32%,
故答案为:5%,40,32%;
(2)补全频数分布直方图如下:
(3)360°×=183.6°,
答:等级为“B”的扇形所对应的圆心角度数为183.6°.
20.(2021秋 宁德期末)为了提升学生的交通安全意识,学校计划开展全员“交通法规”知识竞赛,七(3)班班主任赵老师给全班同学定下的目标是:合格率达90%,优秀率达25%(x<60为不合格;x≥60为合格;x≥90为优秀),为了解班上学生对“交通法规”知识的认知情况,赵老师组织了一次模拟测试,将全班同学的测试成绩整理后作出如下频数分布直方图.(图中的70~80表示70≤x<80,其余类推)
(1)七(3)班共有多少名学生?
(2)赵老师对本次模拟测试结果不满意,请通过计算给出一条她不满意的理由;
(3)模拟测试后,通过强化教育,班级在学校“交通法规”竞赛中成绩有了较大提高,结果优秀人数占合格人数的,比不合格人数多10人.本次竞赛结果是否完成了赵老师预设的目标?请说明理由.
【解析】解:(1)由直方图可得,
4+6+9+10+12+9=50(名),
即七(3)班共有50名学生;
(2)合格率为:×100%=80%,
优秀率为:×100%=18%,
故赵老师不满意的理由是:及格率小于赵老师给全班同学定下的目标(或优秀率小于赵老师给全班同学定下的目标);
(3)设优秀的学生有x人,则合格的学生有3x人,不及格的学生有(x﹣10)人,
3x+(x﹣10)=50,
解得x=15,
∴优秀的学生有15人,则合格的学生有45人,不及格的学生有5人,
∴及格率为:×100%=90%,优秀率为:×100%=30%,
故本次竞赛结果完成了赵老师预设的目标,因为及格率与赵老师给全班同学定下的目标一样,而优秀率高于赵老师给全班同学定下的目标.
21.(2021秋 中原区校级期末)4月23日是“世界读书日”,我校校团委发起了“让阅读成为习惯”的读书活动,鼓励学生利用周末积极阅读课外书籍.为了解学生周末两天的读书时间,校团委随机调查了部分学生的读书时间x(单位:分钟),把读书时间分为四组:A(30≤x<60),B(60≤x<90),C(90≤x<120),D(120≤x<150).部分数据信息如下:
a.B组和C组的所有数据:85 90 60 70 110 75 65 78 100 90 80 95 90
b.根据调查结果绘制了如下尚不完整的统计图:
请根据以上信息,回答下列问题:
(1)被调查的学生共有 20 人,并补全频数分布直方图;
(2)在扇形统计图中,C组所对应的扇形圆心角是 108° ;
(3)请结合统计图给全校学生发出一条合理化的倡议.
【解析】解:(1)4÷20%=20(人),B组人数为7人,D组人数为20﹣4﹣7﹣6=3(人),
故答案为:20,补全频数分布直方图如下:
(2)360°×=108°,
故答案为:108°;
(3)增强读书意识,增加读书时长和阅读量.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
浙教版七年级下 6.5频数直方图同步练习
一.选择题
1.(2021秋 金水区校级期末)某学校在植树节派出50名学生参与植树,统计每个人植树的棵数之后,绘制出如图所示的频数分布直方图(图中分组含最小值,不含最大值),则植树不足7棵的人数占总人数的( )
A.40% B.64% C.24% D.96%
2.(2021秋 兴庆区期末)某养羊场对200只羊质量进行统计,得到频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在77.5kg及以上的生羊的只数是( )
A.180 B.140 C.120 D.110
3.(2021秋 武侯区期末)2021年“世界水日”的主题为“珍惜水、爱护水”.小明家安装节水龙头后,他记录了50天的日用水量数据(单位:m3),得到频数分布表如表:
日用水量x 0≤x<0.1 0.1≤x<0.2 0.2≤x<0.3 0.3≤x<0.4 0.4≤x<0.5 0.5≤x<0.6
频数 2 3 5 20 15 5
在记录的这50天中,日用水量小于0.4m3的频率为( )
A.0.9 B.0.6 C.0.3 D.0.2
4.(2021秋 礼泉县期末)某校九年级随机抽查一部分学生进行了1分钟仰卧起坐次数的测试,并将其绘制成如图所示的频数分布直方图.那么仰卧起坐次数在25~30次的人数占抽查总人数的百分比是( )
A.40% B.30% C.20% D.10%
5.(2022 金华模拟)如图,是九(1)班45名同学每周课外阅读时间的频数分布直方图(每组含前一个边界值,不含后一个边界值),由图可知,每周课外阅读时间不小于6小时的人数是( )
A.6人 B.8人 C.14人 D.36人
6.(2022春 正定县期中)某校为了了解学生在校午餐所需的时间,抽量了20名学生在校午餐所需时间,获得如下的数据(单位:分):10、12、15、10、16、18、19、18、20、18、18、20、28、22、30、20、15、16、21、16.若将这些数据以4分为组距进行分组,则组数是( )
A.4组 B.5组 C.6组 D.7组
7.(2021春 荣县校级期中)在频数分布直方图中,用来表示各组频数的是每个矩形的( )
A.长 B.宽(高) C.周长 D.面积
8.(2021 孝义市三模)根据我国国民倾向的阅读形式的调查研究发现,36.7%的成年国民倾向于“拿一本纸质图书阅读”,有43.5%的国民倾向于“手机阅读”,有10.6%的国民更倾向于“网络在线阅读”,有7.8%的人倾向于“在电子阅读器上阅读”,有1.4%的国民“习惯从网上下载并打印下来阅读”.以上数据最适合用下列哪种统计图描述( )
A.条形统计图 B.折线图
C.频数分布直方图 D.扇形统计图
9.(2021 河东区二模)如图,其中产品净重的范围是[96,106](即96≤净重≤106),样本数据分组为[96,98)(即96≤净重<98)以下类似,[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
A.90 B.75 C.60 D.45
10.(2021春 博兴县期末)某班对学生的一次数学测试成绩(得分取整数)进行整理后分成五组,并绘制出如图所示的频数分布直方图,则下列说法中错误的是( )
A.有6人的成绩为100分
B.这次共有48人参加测试
C.测试成绩高于70分且不高于80分的人数最多
D.若成绩在80分以上为优秀,则成绩优秀的有15人
二.填空题
11.(2021秋 凤翔县期末)已知一组数据都是整数,其中最大值是242,最小数据是198,若把这组数据分成9个小组,则组距是 .
12.(2021秋 伊川县期末)超市为了制定某个时间段收银台开放方案,统计了这个时间段顾客在收银台排队付款的等待时间,并绘制成如图的频数分布直方图(图中等待时间1﹣2分钟表示大于或等于1分钟而小于2分钟,其它类同),这个时间段内顾客等待时间不少于5分钟的人数为 .
13.(2021秋 禅城区期末)为了了解本校九年级学生的体能情况,随机抽查了其中30名学生,测试1分钟仰卧起坐的次数,并将其绘制成如图所示的频数分布直方图,那么仰卧起坐次数在25~30次的人数占抽查总人数的百分比是 .
14.(2021春 海州区期中)将一批数据分成3组,列出分布表,其中第一组与第二组的频率之和是0.67,那么第三组的频率是 .
15.(2021 西山区二模)为了庆祝中国共产党建党100周年,某中学举办了党史知识大赛,赛后随机抽取了部分试卷进行了相关统计,整理并绘制成如下频数分布直方图.本次调查属于 调查,抽取了 人.
16.(2021 瑞安市模拟)某班级对40位学生的一分钟仰卧起坐测试成绩进行统计,得到频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩在35次及以上的学生有 人.
三.解答题
17.(2021秋 河源期末)某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图:
根据图中提供的信息,解答下列问题:
(1)m= ,E组对应的圆心角度数为 °;
(2)补全频数分布直方图.
18.(2022春 泾阳县月考)某校为了提高学生学习国学的积极性,举办了首届“国学知识大赛”,该校所有学生均参加初赛.初赛中,将国学相关知识设置为100分试卷,学生的分数均为50分以上,为了解学生对国学的掌握情况,学校抽取了一部分学生成绩,绘制出不完整的表格和频数分布直方图.
成绩x(分) 频数(人数) 百分比
50<x≤60 2 4%
60<x≤70 10 b
70<x≤80 14 28%
80<x≤90 a 32%
90<x≤100 8 16%
请根据表格提供的信息,解答以下问题:
(1)学校共抽取了 名学生;
(2)求出a、b的值,并补全频数分布直方图;
(3)若将调查结果绘制成扇形统计图,求成绩在“60<x≤70”所对应的扇形圆心角的度数.
19.(2021秋 秦都区期末)某市七年级有3000名学生参加网上“爱我中华知识竞赛”活动,为了解本次知识竞赛成绩的分布情况,从中抽取了200名学生的得分进行统计.
成绩x(分) 频数 频率
50≤x<60 10 a
60≤x<70 16 8%
70≤x<80 b 20%
80≤x<90 62 c
90≤x<100 72 36%
请根据不完整的表格,解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)补全如图所示的频数分布直方图;
(3)若将得分转化为等级,规定50≤x<60评为“D”,60≤x<70评为“C”,70≤x<90评为“B”,90≤x<100评为“A”,并按等级“A”、“B”、“C”、“D”将这次调查的结果绘制成扇形统计图,求等级为“B”的扇形所对应的圆心角度数.
20.(2021秋 宁德期末)为了提升学生的交通安全意识,学校计划开展全员“交通法规”知识竞赛,七(3)班班主任赵老师给全班同学定下的目标是:合格率达90%,优秀率达25%(x<60为不合格;x≥60为合格;x≥90为优秀),为了解班上学生对“交通法规”知识的认知情况,赵老师组织了一次模拟测试,将全班同学的测试成绩整理后作出如下频数分布直方图.(图中的70~80表示70≤x<80,其余类推)
(1)七(3)班共有多少名学生?
(2)赵老师对本次模拟测试结果不满意,请通过计算给出一条她不满意的理由;
(3)模拟测试后,通过强化教育,班级在学校“交通法规”竞赛中成绩有了较大提高,结果优秀人数占合格人数的,比不合格人数多10人.本次竞赛结果是否完成了赵老师预设的目标?请说明理由.
21.(2021秋 中原区校级期末)4月23日是“世界读书日”,我校校团委发起了“让阅读成为习惯”的读书活动,鼓励学生利用周末积极阅读课外书籍.为了解学生周末两天的读书时间,校团委随机调查了部分学生的读书时间x(单位:分钟),把读书时间分为四组:A(30≤x<60),B(60≤x<90),C(90≤x<120),D(120≤x<150).部分数据信息如下:
a.B组和C组的所有数据:85 90 60 70 110 75 65 78 100 90 80 95 90
b.根据调查结果绘制了如下尚不完整的统计图:
请根据以上信息,回答下列问题:
(1)被调查的学生共有 人,并补全频数分布直方图;
(2)在扇形统计图中,C组所对应的扇形圆心角是 ;
(3)请结合统计图给全校学生发出一条合理化的倡议.
答案与解析
一.选择题
1.(2021秋 金水区校级期末)某学校在植树节派出50名学生参与植树,统计每个人植树的棵数之后,绘制出如图所示的频数分布直方图(图中分组含最小值,不含最大值),则植树不足7棵的人数占总人数的( )
A.40% B.64% C.24% D.96%
【解析】解:由图形知,植树不足7棵的人数占总人数的百分比为×100%=24%,
故选:C.
2.(2021秋 兴庆区期末)某养羊场对200只羊质量进行统计,得到频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在77.5kg及以上的生羊的只数是( )
A.180 B.140 C.120 D.110
【解析】解:90+30+20=140(只),
故选:B.
3.(2021秋 武侯区期末)2021年“世界水日”的主题为“珍惜水、爱护水”.小明家安装节水龙头后,他记录了50天的日用水量数据(单位:m3),得到频数分布表如表:
日用水量x 0≤x<0.1 0.1≤x<0.2 0.2≤x<0.3 0.3≤x<0.4 0.4≤x<0.5 0.5≤x<0.6
频数 2 3 5 20 15 5
在记录的这50天中,日用水量小于0.4m3的频率为( )
A.0.9 B.0.6 C.0.3 D.0.2
【解析】解:由表可知,使用后,50天日用水量少于0.4的频数为2+3+5+20=30,
所以估计50天日用水量少于0.4的概率为=0.6.
故选:B.
4.(2021秋 礼泉县期末)某校九年级随机抽查一部分学生进行了1分钟仰卧起坐次数的测试,并将其绘制成如图所示的频数分布直方图.那么仰卧起坐次数在25~30次的人数占抽查总人数的百分比是( )
A.40% B.30% C.20% D.10%
【解析】解:仰卧起坐次数在25~30次的人数占抽查总人数的百分比是×100%=40%,
故选:A.
5.(2022 金华模拟)如图,是九(1)班45名同学每周课外阅读时间的频数分布直方图(每组含前一个边界值,不含后一个边界值),由图可知,每周课外阅读时间不小于6小时的人数是( )
A.6人 B.8人 C.14人 D.36人
【解析】解:由频数分布直方图知,每周课外阅读时间不小于6小时的人数是8+6=14(人),
故选:C.
6.(2022春 正定县期中)某校为了了解学生在校午餐所需的时间,抽量了20名学生在校午餐所需时间,获得如下的数据(单位:分):10、12、15、10、16、18、19、18、20、18、18、20、28、22、30、20、15、16、21、16.若将这些数据以4分为组距进行分组,则组数是( )
A.4组 B.5组 C.6组 D.7组
【解析】解:根据组数=(最大值﹣最小值)÷组距(小数部分要进位),
则(30﹣10)÷4=5,
所以组数为5+1=6.
故选:C.
7.(2021春 荣县校级期中)在频数分布直方图中,用来表示各组频数的是每个矩形的( )
A.长 B.宽(高) C.周长 D.面积
【解析】解:在频数分布直方图中,用来表示各组频数的是每个矩形的面积.
故选:D.
8.(2021 孝义市三模)根据我国国民倾向的阅读形式的调查研究发现,36.7%的成年国民倾向于“拿一本纸质图书阅读”,有43.5%的国民倾向于“手机阅读”,有10.6%的国民更倾向于“网络在线阅读”,有7.8%的人倾向于“在电子阅读器上阅读”,有1.4%的国民“习惯从网上下载并打印下来阅读”.以上数据最适合用下列哪种统计图描述( )
A.条形统计图 B.折线图
C.频数分布直方图 D.扇形统计图
【解析】解:由题意,用扇形统计图,可以描述国民阅读形式的百分比.
故选:D.
9.(2021 河东区二模)如图,其中产品净重的范围是[96,106](即96≤净重≤106),样本数据分组为[96,98)(即96≤净重<98)以下类似,[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
A.90 B.75 C.60 D.45
【解析】解:∵样本中产品净重小于100克的个数是36,其对应频率之和为:0.05×2+0.1×2=0.3,
∴样本总数为:36÷0.3=120,
∴样本中净重大于或等于98克并且小于104克的产品的个数是:120×(0.1×2+0.15×2+0.125×2)=90.
故选:A.
10.(2021春 博兴县期末)某班对学生的一次数学测试成绩(得分取整数)进行整理后分成五组,并绘制出如图所示的频数分布直方图,则下列说法中错误的是( )
A.有6人的成绩为100分
B.这次共有48人参加测试
C.测试成绩高于70分且不高于80分的人数最多
D.若成绩在80分以上为优秀,则成绩优秀的有15人
【解析】解:A、由图可知90.5~100.5组的有6人,不一定都是100分,此选项错误;
B、这次活动共抽调了3+12+18+9+6=48人测试,此选项正确;
C、测试成绩在70﹣80分的人数为18人,最多,此选项正确;
D、测试成绩在80分以上的人数为15人,此选项正确;
故选:A.
二.填空题
11.(2021秋 凤翔县期末)已知一组数据都是整数,其中最大值是242,最小数据是198,若把这组数据分成9个小组,则组距是 5 .
【解析】解:这组数据的极差为242﹣198=44,
44÷9≈4.9,
所以组距为5,
故答案为:5.
12.(2021秋 伊川县期末)超市为了制定某个时间段收银台开放方案,统计了这个时间段顾客在收银台排队付款的等待时间,并绘制成如图的频数分布直方图(图中等待时间1﹣2分钟表示大于或等于1分钟而小于2分钟,其它类同),这个时间段内顾客等待时间不少于5分钟的人数为 16 .
【解析】解:由直方图可得,
这个时间段内顾客等待时间不少于5分钟的人数为:9+5+2=16,
故答案为:16.
13.(2021秋 禅城区期末)为了了解本校九年级学生的体能情况,随机抽查了其中30名学生,测试1分钟仰卧起坐的次数,并将其绘制成如图所示的频数分布直方图,那么仰卧起坐次数在25~30次的人数占抽查总人数的百分比是 40% .
【解析】解:×100%=40%,
即仰卧起坐次数在25~30次的人数占抽查总人数的百分比是40%,
故答案为:40%.
14.(2021春 海州区期中)将一批数据分成3组,列出分布表,其中第一组与第二组的频率之和是0.67,那么第三组的频率是 0.33 .
【解析】解:第三组的频率是:1﹣0.67=0.33;
故答案为:0.33.
15.(2021 西山区二模)为了庆祝中国共产党建党100周年,某中学举办了党史知识大赛,赛后随机抽取了部分试卷进行了相关统计,整理并绘制成如下频数分布直方图.本次调查属于 抽样调查 调查,抽取了 100 人.
【解析】解:为了庆祝中国共产党建党100周年,某中学举办了党史知识大赛,赛后随机抽取了部分试卷进行了相关统计,整理并绘制成如下频数分布直方图.
本次调查属于抽样调查,抽取了:10+15+20+40+15=100(人).
故答案为:抽样调查;100.
16.(2021 瑞安市模拟)某班级对40位学生的一分钟仰卧起坐测试成绩进行统计,得到频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩在35次及以上的学生有 16 人.
【解析】解:由直方图可得,
成绩为在35次及以上的学生有:10+6=16(人),
故答案为:16.
三.解答题
17.(2021秋 河源期末)某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分布直方图和扇形统计图:
根据图中提供的信息,解答下列问题:
(1)m= 40 ,E组对应的圆心角度数为 14.4 °;
(2)补全频数分布直方图.
【解析】解:(1)本次调查的人数为:10÷10%=100,
m%=40÷100×100%=40%,
∴m=40,
E组对应的圆心角度数为:(1﹣21%﹣40%﹣25%﹣10%)×360°=14.4°,
故答案为:40,14.4;
(2)D组的频数为:100×25%=25,
补全的频数分布直方图如图所示;
.
18.(2022春 泾阳县月考)某校为了提高学生学习国学的积极性,举办了首届“国学知识大赛”,该校所有学生均参加初赛.初赛中,将国学相关知识设置为100分试卷,学生的分数均为50分以上,为了解学生对国学的掌握情况,学校抽取了一部分学生成绩,绘制出不完整的表格和频数分布直方图.
成绩x(分) 频数(人数) 百分比
50<x≤60 2 4%
60<x≤70 10 b
70<x≤80 14 28%
80<x≤90 a 32%
90<x≤100 8 16%
请根据表格提供的信息,解答以下问题:
(1)学校共抽取了 50 名学生;
(2)求出a、b的值,并补全频数分布直方图;
(3)若将调查结果绘制成扇形统计图,求成绩在“60<x≤70”所对应的扇形圆心角的度数.
【解析】解:(1)由表格可得,
本次决赛的学生数为:10÷0.2=50,
故答案为:50;
(2)a=50×0.32=16,b=10÷50=20%,
补全的频数分布直方图如右图所示,
(3)360°×20%=72°,
故成绩在“60<x≤70”所对应的扇形圆心角的度数为72°.
19.(2021秋 秦都区期末)某市七年级有3000名学生参加网上“爱我中华知识竞赛”活动,为了解本次知识竞赛成绩的分布情况,从中抽取了200名学生的得分进行统计.
成绩x(分) 频数 频率
50≤x<60 10 a
60≤x<70 16 8%
70≤x<80 b 20%
80≤x<90 62 c
90≤x<100 72 36%
请根据不完整的表格,解答下列问题:
(1)填空:a= 5% ,b= 40 ,c= 31% ;
(2)补全如图所示的频数分布直方图;
(3)若将得分转化为等级,规定50≤x<60评为“D”,60≤x<70评为“C”,70≤x<90评为“B”,90≤x<100评为“A”,并按等级“A”、“B”、“C”、“D”将这次调查的结果绘制成扇形统计图,求等级为“B”的扇形所对应的圆心角度数.
【解析】解:(1)调查总人数为16÷8%=200(人),
∴a=10÷200×100%=5%,b=200×20%=40(人),c=62÷200×100%=32%,
故答案为:5%,40,32%;
(2)补全频数分布直方图如下:
(3)360°×=183.6°,
答:等级为“B”的扇形所对应的圆心角度数为183.6°.
20.(2021秋 宁德期末)为了提升学生的交通安全意识,学校计划开展全员“交通法规”知识竞赛,七(3)班班主任赵老师给全班同学定下的目标是:合格率达90%,优秀率达25%(x<60为不合格;x≥60为合格;x≥90为优秀),为了解班上学生对“交通法规”知识的认知情况,赵老师组织了一次模拟测试,将全班同学的测试成绩整理后作出如下频数分布直方图.(图中的70~80表示70≤x<80,其余类推)
(1)七(3)班共有多少名学生?
(2)赵老师对本次模拟测试结果不满意,请通过计算给出一条她不满意的理由;
(3)模拟测试后,通过强化教育,班级在学校“交通法规”竞赛中成绩有了较大提高,结果优秀人数占合格人数的,比不合格人数多10人.本次竞赛结果是否完成了赵老师预设的目标?请说明理由.
【解析】解:(1)由直方图可得,
4+6+9+10+12+9=50(名),
即七(3)班共有50名学生;
(2)合格率为:×100%=80%,
优秀率为:×100%=18%,
故赵老师不满意的理由是:及格率小于赵老师给全班同学定下的目标(或优秀率小于赵老师给全班同学定下的目标);
(3)设优秀的学生有x人,则合格的学生有3x人,不及格的学生有(x﹣10)人,
3x+(x﹣10)=50,
解得x=15,
∴优秀的学生有15人,则合格的学生有45人,不及格的学生有5人,
∴及格率为:×100%=90%,优秀率为:×100%=30%,
故本次竞赛结果完成了赵老师预设的目标,因为及格率与赵老师给全班同学定下的目标一样,而优秀率高于赵老师给全班同学定下的目标.
21.(2021秋 中原区校级期末)4月23日是“世界读书日”,我校校团委发起了“让阅读成为习惯”的读书活动,鼓励学生利用周末积极阅读课外书籍.为了解学生周末两天的读书时间,校团委随机调查了部分学生的读书时间x(单位:分钟),把读书时间分为四组:A(30≤x<60),B(60≤x<90),C(90≤x<120),D(120≤x<150).部分数据信息如下:
a.B组和C组的所有数据:85 90 60 70 110 75 65 78 100 90 80 95 90
b.根据调查结果绘制了如下尚不完整的统计图:
请根据以上信息,回答下列问题:
(1)被调查的学生共有 20 人,并补全频数分布直方图;
(2)在扇形统计图中,C组所对应的扇形圆心角是 108° ;
(3)请结合统计图给全校学生发出一条合理化的倡议.
【解析】解:(1)4÷20%=20(人),B组人数为7人,D组人数为20﹣4﹣7﹣6=3(人),
故答案为:20,补全频数分布直方图如下:
(2)360°×=108°,
故答案为:108°;
(3)增强读书意识,增加读书时长和阅读量.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
