浙教版数学七年级下册 第3章 杨辉三角与两数和的乘方 课件(共23张PPT)
文档属性
| 名称 | 浙教版数学七年级下册 第3章 杨辉三角与两数和的乘方 课件(共23张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-30 16:55:52 | ||
图片预览

文档简介
(共23张PPT)
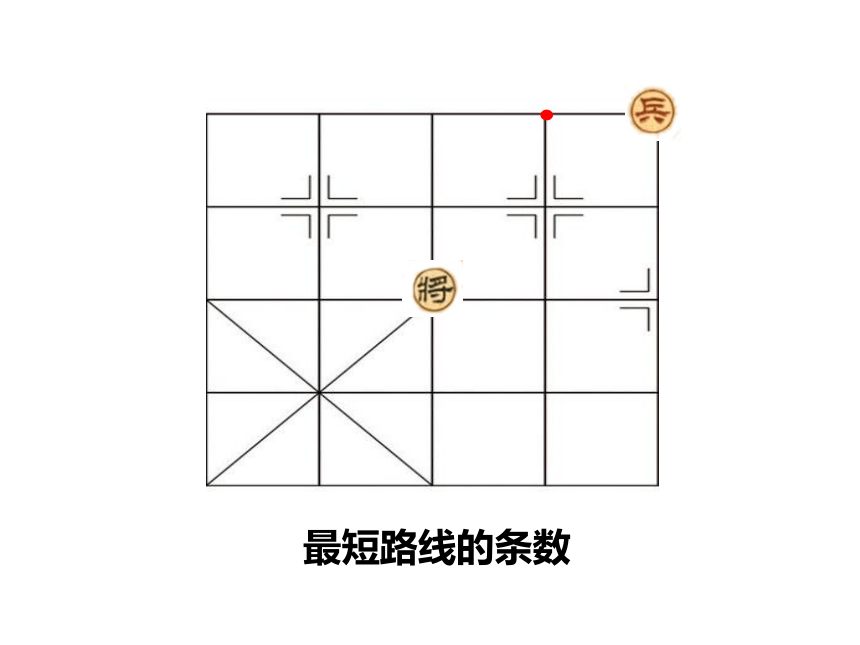
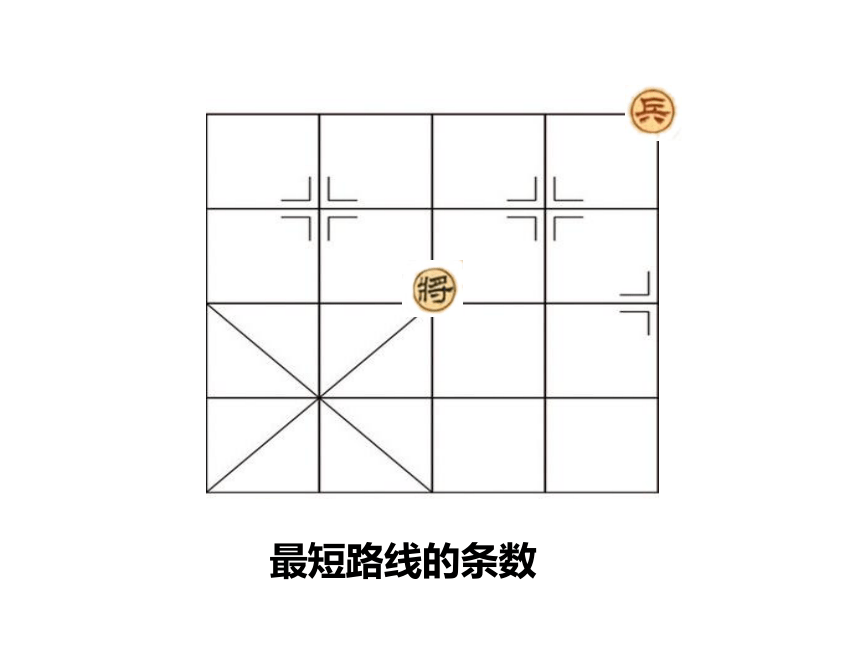
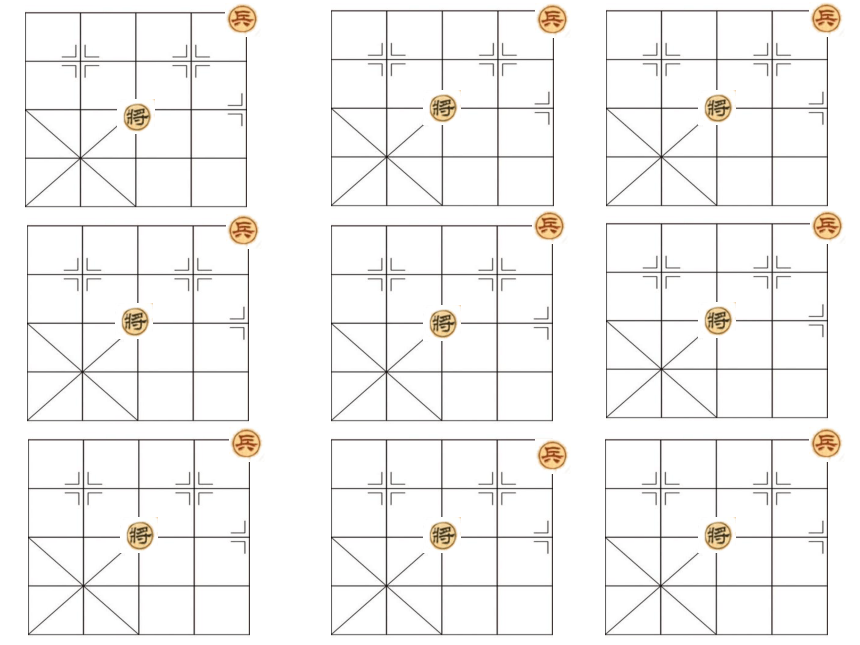
最短路线的条数
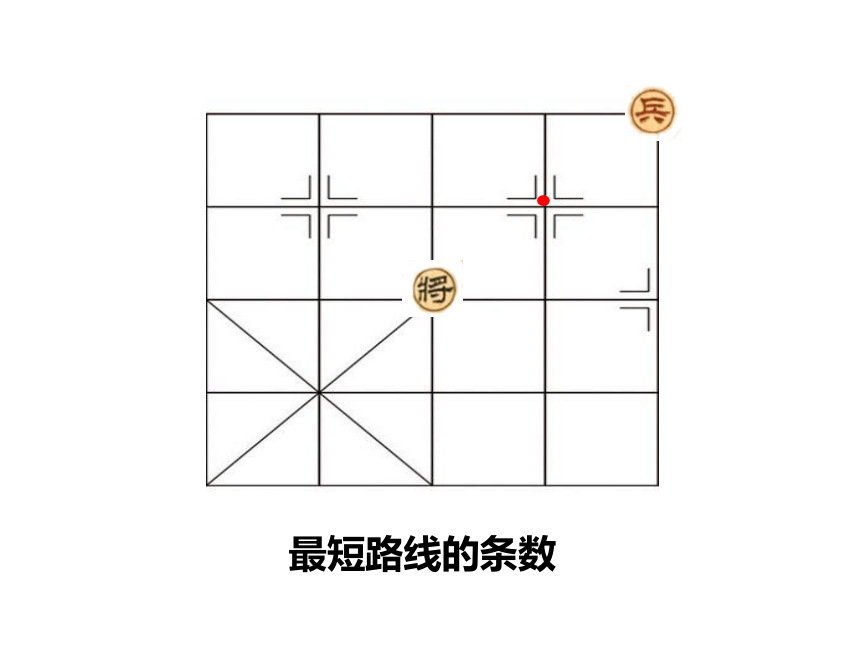
最短路线的条数
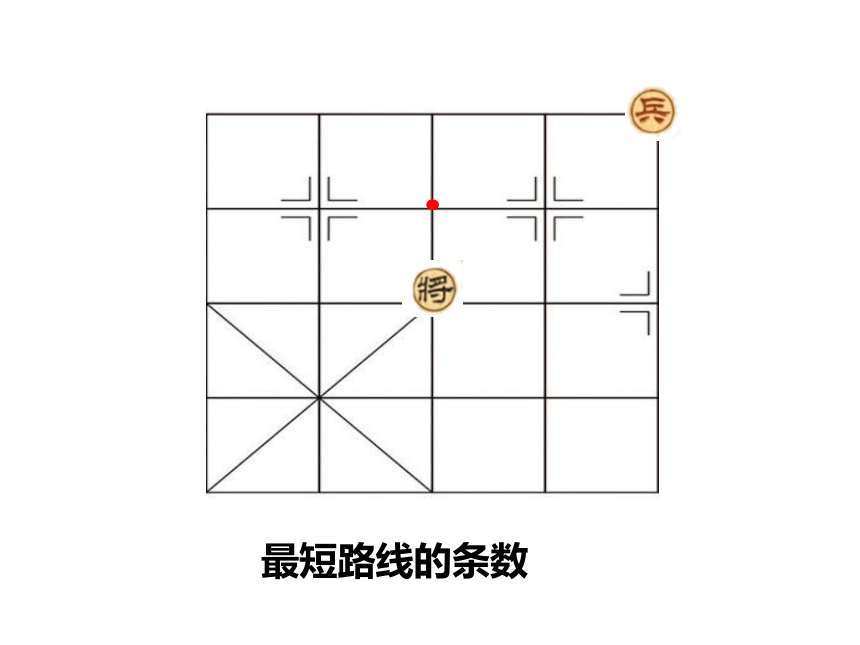
最短路线的条数
最短路线的条数
1
1
1
1
1
1
1
1
2
3
3
4
4
6
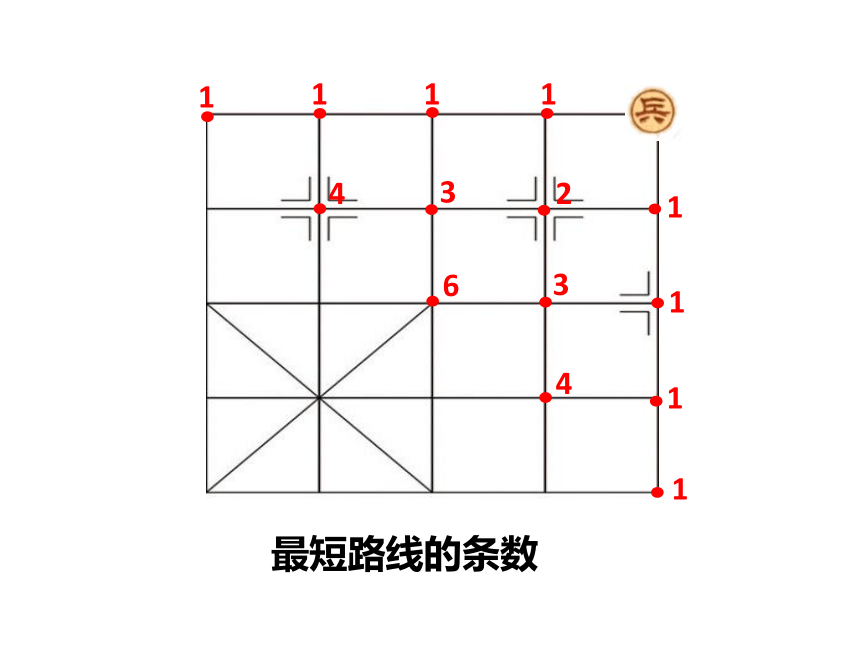
最短路线的条数
1
1
1
1
1
1
1
1
2
3
3
4
4
6
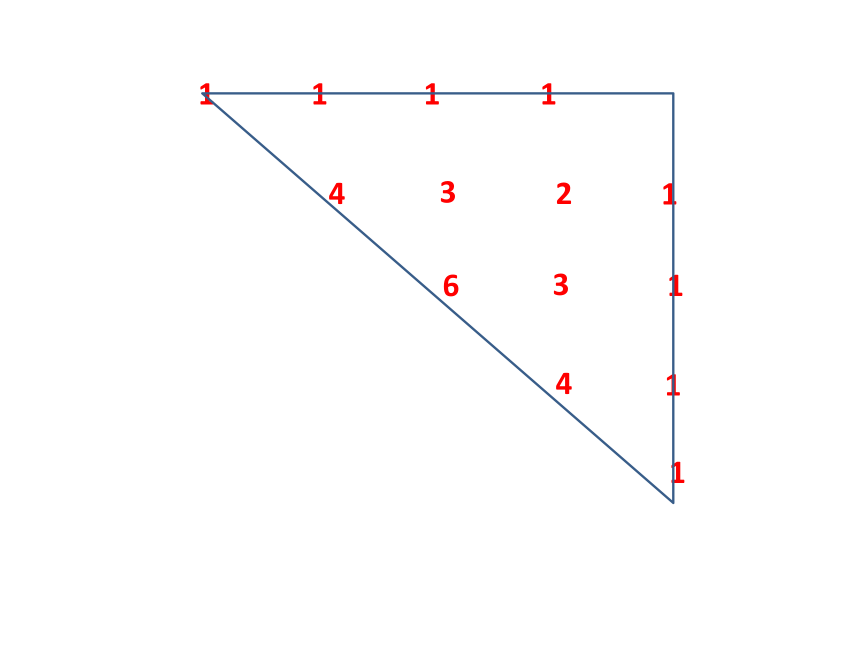
1
1
1
1
1
1
1
1
2
3
3
4
4
6
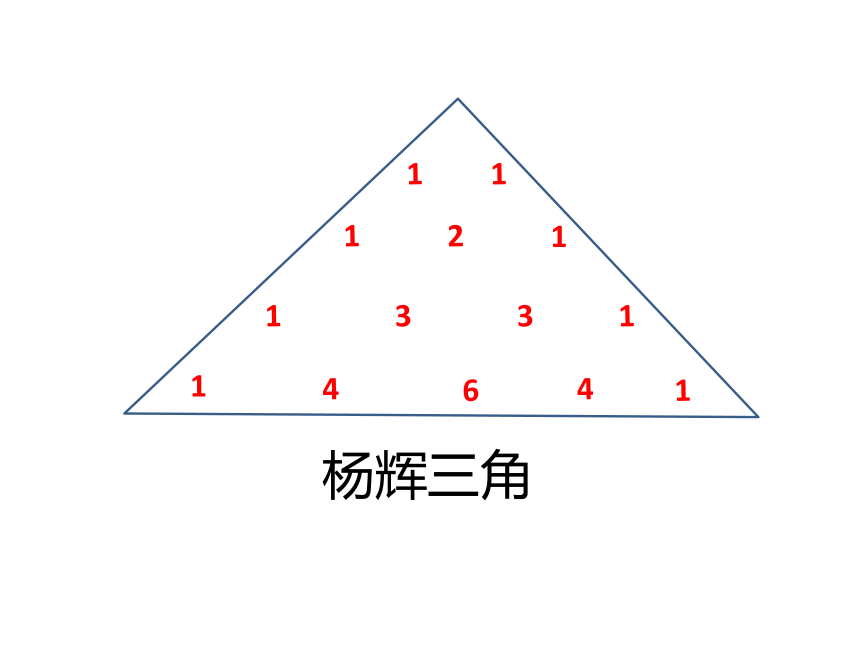
杨辉三角
这样的表,在我国南宋数学家杨辉1261 年所著的《详解九章算术》一书中已有记载。并说明此图源于北宋数学家贾宪(约公元11世纪)的
“开方作法本原图” .然而,在欧洲,这个表被认为是法国数学家物理学家帕斯卡首先发现的,他们把这个表叫做帕斯卡三角.其实,杨辉三角的发现要比欧洲早500年左右.
例1:计算
练习1:计算
变式1:求中项的系数
可以被2整除吗?
转化
赋值法
今天是星期四 ,再过后是星期几?
变式1:今天是星期四,再过后是星期几?
例2:今天是星期四 ,再过后是星期几?
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
………………………………
第1行
第2行
第3行
第4行
第5行
第6行
第7行
第8行
规律探究
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
………………………………
第1行
第2行
第3行
第4行
第5行
第6行
第7行
第8行
杨辉三角第行(n是正整数)的各
个数都是奇数
横行规律
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
………………………………
第1行
第2行
第3行
第4行
第5行
第6行
第7行
第8行
横行规律
杨辉三角第1行(n是正整数)除两端的1之外都是偶数
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
………………………………
第1行
第2行
第3行
第4行
第5行
第6行
第7行
第8行
横行规律
杨辉三角第n 行(n是正整数)的和是
+
+
+
+
+
+
+
+
+
+
4
8
16
1
2
=22
=23
=24
=20
=21
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
………………………………
第1行
第2行
第3行
第4行
第5行
第6行
第7行
第8行
斜行规律
杨辉三角第n行第2个数比第n-1行第2个数大1
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
………………………………
第1行
第2行
第3行
第4行
第5行
第6行
第7行
第8行
斜行规律
杨辉三角第n行第三个数比第n-1行第三个数大n-2
三角形数
1
1
1
1
1
1
1
1
2
3
3
4
4
6
5
5
10
10
15
15
20
35
35
70
通过这节课的学习
我学会了……知识
我的收获
我掌握了……方法
我运用了……数学思想方法
作业
1、阅读《从杨辉三角谈起》
2、查阅网上资料并结合本节课所学知识,写一篇关于杨辉三角规律探究和实际应用的小论文
再
见
最短路线的条数
最短路线的条数
最短路线的条数
最短路线的条数
1
1
1
1
1
1
1
1
2
3
3
4
4
6
最短路线的条数
1
1
1
1
1
1
1
1
2
3
3
4
4
6
1
1
1
1
1
1
1
1
2
3
3
4
4
6
杨辉三角
这样的表,在我国南宋数学家杨辉1261 年所著的《详解九章算术》一书中已有记载。并说明此图源于北宋数学家贾宪(约公元11世纪)的
“开方作法本原图” .然而,在欧洲,这个表被认为是法国数学家物理学家帕斯卡首先发现的,他们把这个表叫做帕斯卡三角.其实,杨辉三角的发现要比欧洲早500年左右.
例1:计算
练习1:计算
变式1:求中项的系数
可以被2整除吗?
转化
赋值法
今天是星期四 ,再过后是星期几?
变式1:今天是星期四,再过后是星期几?
例2:今天是星期四 ,再过后是星期几?
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
………………………………
第1行
第2行
第3行
第4行
第5行
第6行
第7行
第8行
规律探究
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
………………………………
第1行
第2行
第3行
第4行
第5行
第6行
第7行
第8行
杨辉三角第行(n是正整数)的各
个数都是奇数
横行规律
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
………………………………
第1行
第2行
第3行
第4行
第5行
第6行
第7行
第8行
横行规律
杨辉三角第1行(n是正整数)除两端的1之外都是偶数
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
………………………………
第1行
第2行
第3行
第4行
第5行
第6行
第7行
第8行
横行规律
杨辉三角第n 行(n是正整数)的和是
+
+
+
+
+
+
+
+
+
+
4
8
16
1
2
=22
=23
=24
=20
=21
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
………………………………
第1行
第2行
第3行
第4行
第5行
第6行
第7行
第8行
斜行规律
杨辉三角第n行第2个数比第n-1行第2个数大1
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
………………………………
第1行
第2行
第3行
第4行
第5行
第6行
第7行
第8行
斜行规律
杨辉三角第n行第三个数比第n-1行第三个数大n-2
三角形数
1
1
1
1
1
1
1
1
2
3
3
4
4
6
5
5
10
10
15
15
20
35
35
70
通过这节课的学习
我学会了……知识
我的收获
我掌握了……方法
我运用了……数学思想方法
作业
1、阅读《从杨辉三角谈起》
2、查阅网上资料并结合本节课所学知识,写一篇关于杨辉三角规律探究和实际应用的小论文
再
见
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
