浙江省2021—2022学年浙教版数学七年级下册 第1章 平行线 期末考试专题练 (word版、含解析)
文档属性
| 名称 | 浙江省2021—2022学年浙教版数学七年级下册 第1章 平行线 期末考试专题练 (word版、含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 315.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 16:37:39 | ||
图片预览


文档简介
2022年浙江省七年级下册数学期末考试专题练-第1章《平行线》(2)
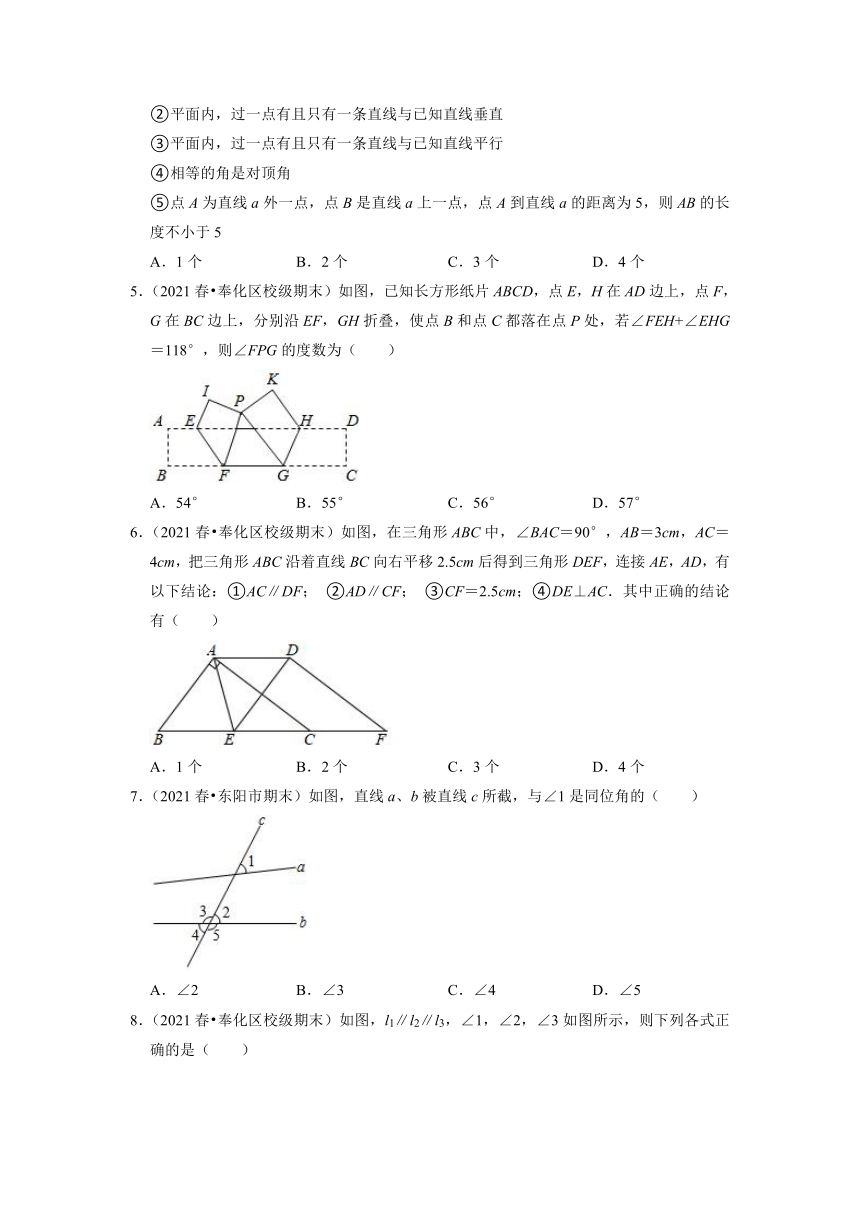
一.选择题(共13小题)
1.(2021春 西湖区期末)如图,AB∥DE,BC⊥CD,则以下说法中正确的是( )
A.α,β的角度数之和为定值
B.α随β增大而增大
C.α,β的角度数之积为定值
D.α随β增大而减小
2.(2021 宁波模拟)如图,所有角均为直角,所有线段均不相等,若要知道该图形周长,至少需要知道几条线段的长( )
A.3条 B.4条 C.5条 D.6条
3.(2021春 奉化区校级期末)如图所示,直线a∥b,直线c与直线a,b分别交于点D,E,射线DF⊥直线c,若∠1=32°,则∠2的度数是( )
A.67° B.48° C.32° D.58°
4.(2021春 奉化区校级期末)下列说法正确的有( )
①两条直线被第三条直线所截,内错角相等
②平面内,过一点有且只有一条直线与已知直线垂直
③平面内,过一点有且只有一条直线与已知直线平行
④相等的角是对顶角
⑤点A为直线a外一点,点B是直线a上一点,点A到直线a的距离为5,则AB的长度不小于5
A.1个 B.2个 C.3个 D.4个
5.(2021春 奉化区校级期末)如图,已知长方形纸片ABCD,点E,H在AD边上,点F,G在BC边上,分别沿EF,GH折叠,使点B和点C都落在点P处,若∠FEH+∠EHG=118°,则∠FPG的度数为( )
A.54° B.55° C.56° D.57°
6.(2021春 奉化区校级期末)如图,在三角形ABC中,∠BAC=90°,AB=3cm,AC=4cm,把三角形ABC沿着直线BC向右平移2.5cm后得到三角形DEF,连接AE,AD,有以下结论:①AC∥DF; ②AD∥CF; ③CF=2.5cm;④DE⊥AC.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
7.(2021春 东阳市期末)如图,直线a、b被直线c所截,与∠1是同位角的( )
A.∠2 B.∠3 C.∠4 D.∠5
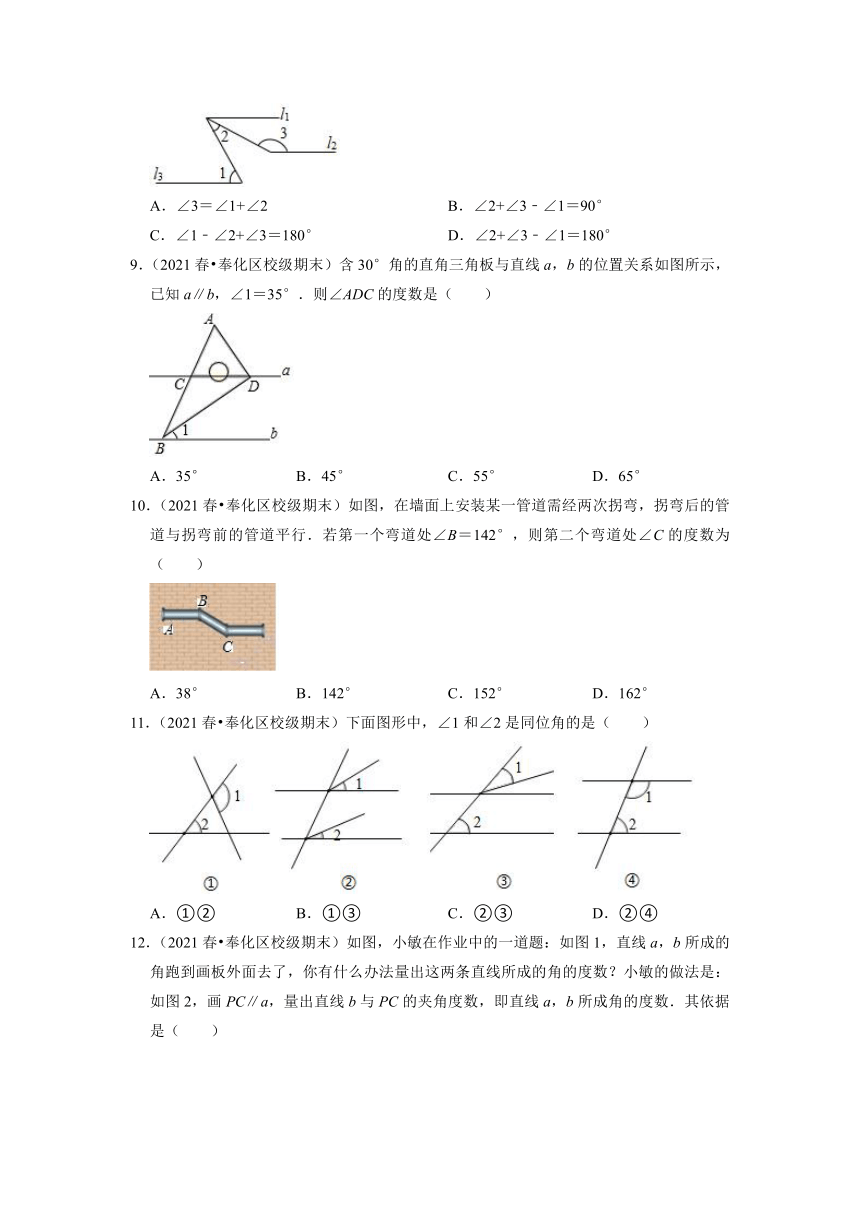
8.(2021春 奉化区校级期末)如图,l1∥l2∥l3,∠1,∠2,∠3如图所示,则下列各式正确的是( )
A.∠3=∠1+∠2 B.∠2+∠3﹣∠1=90°
C.∠1﹣∠2+∠3=180° D.∠2+∠3﹣∠1=180°
9.(2021春 奉化区校级期末)含30°角的直角三角板与直线a,b的位置关系如图所示,已知a∥b,∠1=35°.则∠ADC的度数是( )
A.35° B.45° C.55° D.65°
10.(2021春 奉化区校级期末)如图,在墙面上安装某一管道需经两次拐弯,拐弯后的管道与拐弯前的管道平行.若第一个弯道处∠B=142°,则第二个弯道处∠C的度数为( )
A.38° B.142° C.152° D.162°
11.(2021春 奉化区校级期末)下面图形中,∠1和∠2是同位角的是( )
A.①② B.①③ C.②③ D.②④
12.(2021春 奉化区校级期末)如图,小敏在作业中的一道题:如图1,直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小敏的做法是:如图2,画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数.其依据是( )
A.两直线平行,同位角相等
B.同旁内角互补,两直线平行
C.内错角相等,两直线平行
D.同位角相等,两直线平行
13.(2021春 奉化区校级期末)如图,E在线段BA的延长线上,∠EAD=∠D,∠B=∠D,EF∥HC,连FH交AD于G,∠FGA的余角比∠DGH大16°,K为线段BC上一点,连CG,使∠CKG=∠CGK,在∠AGK内部有射线GM,GM平分∠FGC,则下列结论:①AD∥BC;②GK平分∠AGC;③∠E+∠EAG+∠HCK=180°;④∠MGK的角度为定值且定值为16°,其中正确结论的个数有( )
A.4个 B.3个 C.2个 D.1个
二.填空题(共9小题)
14.(2021春 慈溪市期末)如图,在三角形ABC中,BC=6,把三角形ABC沿射线AB方向平移3个单位至三角形EFG处,EG与BC交于点M.若CM=2,则图中阴影部分的面积为 .
15.(2021春 萧山区期末)如图,将长为acm(a>2),宽为bcm(b>1)的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形A′B′C′D′,则阴影部分的面积为 cm2.(用含a、b的代数式表示,结果要求化成最简)
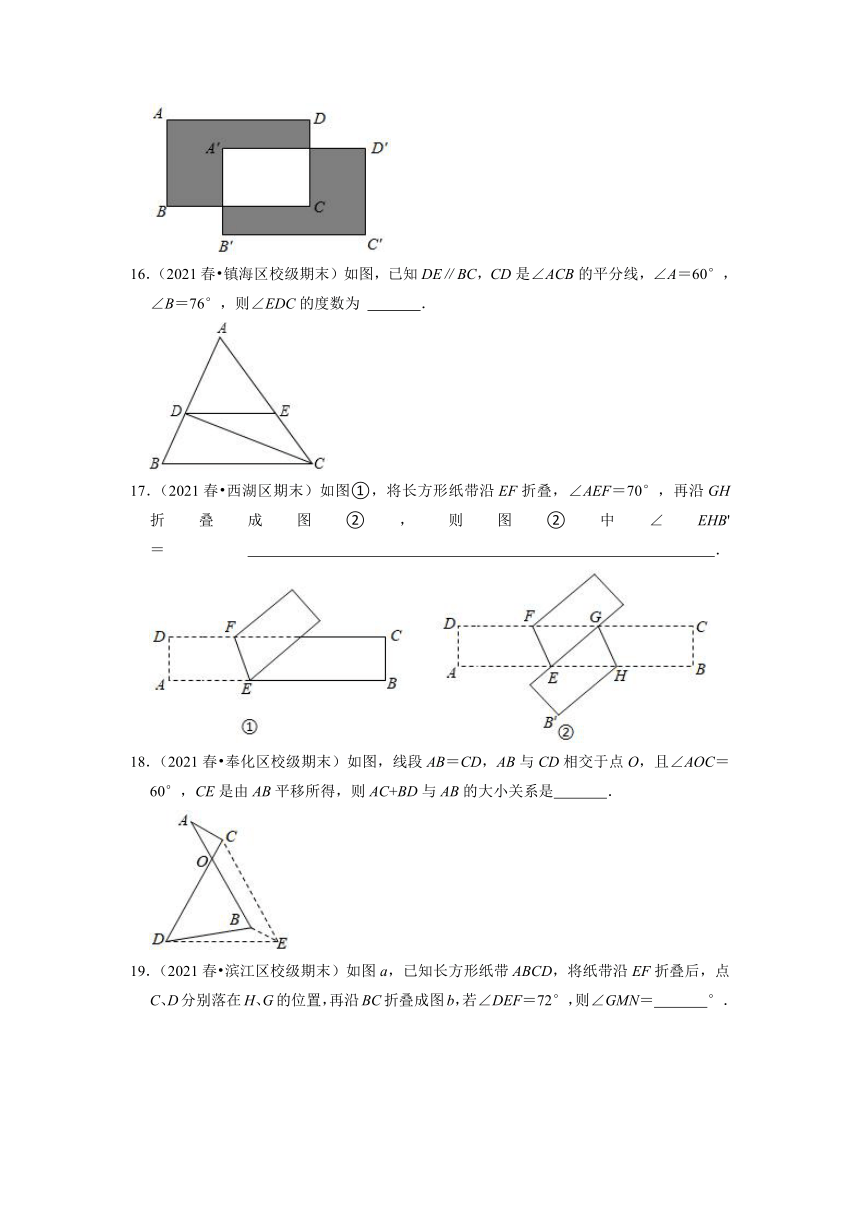
16.(2021春 镇海区校级期末)如图,已知DE∥BC,CD是∠ACB的平分线,∠A=60°,∠B=76°,则∠EDC的度数为 .
17.(2021春 西湖区期末)如图①,将长方形纸带沿EF折叠,∠AEF=70°,再沿GH折叠成图②,则图②中∠EHB'= .
18.(2021春 奉化区校级期末)如图,线段AB=CD,AB与CD相交于点O,且∠AOC=60°,CE是由AB平移所得,则AC+BD与AB的大小关系是 .
19.(2021春 滨江区校级期末)如图a,已知长方形纸带ABCD,将纸带沿EF折叠后,点C、D分别落在H、G的位置,再沿BC折叠成图b,若∠DEF=72°,则∠GMN= °.
20.(2021春 奉化区校级期末)图1是一盏可折叠台灯.图2为其平面示意图,底座AO⊥OE于点O,支架AB,BC为固定支撑杆,∠A是∠B的两倍,灯体CD可绕点C旋转调节.现把灯体CD从水平位置旋转到CD′位置(如图2中虚线所示),此时,灯体CD′所在的直线恰好垂直支架AB,且∠BCD﹣∠DCD′=126°,则∠DCD′= .
21.(2021春 奉化区校级期末)如图,已知AM∥CN,点B为平面内一点,AB⊥BC于B,过点B作BD⊥AM于点D,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,则∠EBC的度数为 .
22.(2021春 奉化区校级期末)如图,C为∠AOB的边OA上一点,过点C作CD∥OB交∠AOB的平分线OE于点F,作CH⊥OB交BO的延长线于点H,若∠EFD=α,现有以下结论:①∠COF=α;②∠AOH=180°﹣2α;③CH⊥CD;④∠OCH=2α﹣90°.其中正确的是 (填序号).
三.解答题(共10小题)
23.(2021春 上城区期末)如图,政府规划由西向东修一条公路.从A修至B后为了绕开村庄,改为沿南偏东25°方向修建BC段,在C处又改变方向修建CD段,测得∠BCD=70°,在D处继续改变方向,朝与出发时相同的方向修至E.
(1)补全施工路线示意图,求∠CDE的度数;
(2)原计划在AB的延长线上依次修建两个公交站M,N(均在CD右侧),连结DM和MN,求∠CDM与∠DMN的数量关系.
24.(2021春 乐清市期末)如图,BF交DE于点C,DE∥AB,∠ABC=∠ADC.
(1)AD与BF平行吗?请说明理由.
(2)若BD平分∠ABC,且∠1+∠2=110°,求∠DCF的度数.
25.(2021春 浦江县期末)如图,已知AB∥CD,AD∥BE,点C在线段BE上,∠BAE=87°,∠E=20°,AE与CD交于点F.
(1)求∠ADC的度数;
(2)连结BF,若∠AFB:∠BFC=1:2,求∠FBC的度数.
26.(2021春 北仑区期末)如图,点O在直线AB上,OC⊥OD,∠D与∠1互余,F是DE上一点,连接OF.
(1)ED是否平行于AB,请说明理由;
(2)若OD平分∠BOF,∠OFD=70°,求∠1的度数.
27.(2021春 椒江区期末)如图:BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H.∠GFH+∠BHC=180°,求证:∠1=∠2.
证明:∵∠BHC=∠FHD,∠GFH+∠BHC=180°,
∴∠GFH+∠FHD=180°
∴FG平行BD
∴
∵BD平分∠ABC,
∴
∴∠1=∠2
28.(2021春 慈溪市期末)如图,直线CD∥EF,点A,B分别在直线CD,EF上(自左至右分别为C,A,D和E,B,F),∠ABF=60°.射线AM自射线AB的位置开始,绕点A以每秒1°的速度沿逆时针方向旋转,同时,射线BN自射线BE开始以每秒5°的速度绕点B沿顺时针方向旋转,当射线BN旋转到BF的位置时,两者停止运动.设旋转时间为x秒.
(1)如图1,直接写出下列答案:
①∠BAD的度数;
②射线BN过点A时的x的值.
(2)如图2,求当AM∥BN时的x的值.
(3)若两条射线AM和BN所在的直线交于点P.
①如图3,若P在CD与EF之间,且∠APB=126°,求x的值.
②若x<24,求∠APB的度数(直接写出用含x的代数式表示的结果).
29.(2021春 江干区期末)已知AM∥BN,BD平分∠ABN交AM于点D,E为射线BA上的点,连接ED交BN于C,设∠ABD=α.
(1)如图1,求∠ADB的度数(用α表示);
(2)如图2,若F为AD上的点,∠EFD的平分线所在直线分别交BD、ED于点G、H,当HG∥BE时,求∠BEF的度数(用α表示).
30.(2021春 拱墅区期末)如图,已知AB∥CD,EG平分∠BEF,FG平分∠EFD.
(1)若∠1=50°,求∠2的度数;
(2)若EH平分∠AEF,判断EH,FG是否平行,并说明理由.
31.(2021春 拱墅区期末)如图,BD是∠ABC的角平分线,∠ABE+∠BCF=180°.
(1)若∠ABC=80°,求∠BCF的值;
(2)求证:DE∥CF;
(3)若CB是∠ACF的角平分线,∠ADB=k∠ABD,求k的值.
32.(2021春 西湖区期末)已知点C在射线OA上.
(1)如图①,CD∥OE,若∠AOB=90°,∠OCD=120°,求∠BOE的度数;
(2)在①中,将射线OE沿射线OB平移得O′E'(如图②),若∠AOB=α,探究∠OCD与∠BO′E′的关系(用含α的代数式表示);
(3)在②中,过点O′作OB的垂线,与∠OCD的平分线交于点P(如图③),若∠CPO′=90°,探究∠AOB与∠BO′E′的关系.
2022年浙江省七年级下册数学期末考试专题练-第1章《平行线》(2)
参考答案与试题解析
一.选择题(共13小题)
1.【解答】解:过C点作MF∥AB,
∵AB∥DE,
∴MF∥DE,
∴∠α=∠BCM,∠β+∠DCM=180°,
∵BC⊥CD,
∴∠BCD=90°,
∴∠BCM+∠DCM=360°﹣∠BCD=270°,
∴∠α+(180°﹣∠β)=270°,
∴∠α﹣∠β=90°,
∴α随β增大而增大,
故选:B.
2.【解答】解:如图:
若要知道该图形周长,至少需要知道4条线段的长:BC、AB,IJ,EF,
∵BC=AL+KJ+IH+GF+DE,AB=LK+KK′=LK+CC′,IJ=HG+GG′=HG+C′D′,EF=DD′,
∴只要知道BC、AB,IJ,EF4条线段的长,就能知道该图形周长.
故选:B.
3.【解答】解:
∵a∥b,
∴∠2=∠3,
∵DF⊥直线c,
∴∠FDE=∠1+∠3=90°,
∵∠1=32°,
∴∠3=90°﹣32°=58°,
∴∠2=58°.
故选:D.
4.【解答】解:①两直线不一定平行,故错误;
②平行公理,故正确;
③必须是过直线外一点,故错误;
④相等的角不一定是对顶角,故错误;
⑤垂线段最短,故正确.
故选:B.
5.【解答】解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠FEH=∠BFE,∠EHG=∠CGH,
∴∠BFE+∠CGH=∠FEH+∠EHG=118°,
由折叠可知:
EF,GH分别是∠BFP和∠CGP的角平分线,
∴∠PFE=∠BFE,∠PGH=∠CGH,
∴∠PFE+∠PGH=∠BFE+∠CGH=118°,
∴∠BFP+∠CGP=2(∠BFE+∠CGH)=236°,
∴∠PFG+∠PGF=360°﹣(∠BFP+∠CGP)=360°﹣236°=124°,
∴∠FPG=180°﹣(∠PFG+∠PGF)=180°﹣124°=56°.
故选:C.
6.【解答】解:∵△ABC沿着直线BC的方向平移2.5cm后得到△DEF,
∴AC∥DF,故①正确;
AD∥CF,故②正确;
CF=AD=2.5cm,故③正确;
AB∥DE,
又∵∠BAC=90°,
∴BA⊥AC,
∴DE⊥AC,故④正确;
故选:D.
7.【解答】解:A、∠2与∠1是同位角,故本选项符合题意;
B、∠3与∠1不是同位角,故本选项不符合题意;
C、∠4与∠1是同位角,故本选项不符合题意;
D、∠5与∠1不是同位角,故本选项不符合题意;
故选:A.
8.【解答】解:∵l1∥l2∥l3,
∴∠1=∠2+∠4,∠4+∠3=180°,
∴∠1﹣∠2+∠3=180°,
故选:C.
9.【解答】解:∵a∥b,
∴∠BDC=∠1=35°.
又∵∠ADB=90°,
∴∠ADC=90°﹣35°=55°.
故选:C.
10.【解答】解:如图所示:
∵拐弯后的管道与拐弯前的管道平行,
∴AB∥CD,
∴∠B=∠C,
又∵∠B=142°,
∴∠C=142°,
故选:B.
11.【解答】解:根据同位角的定义,可得图①中,∠1与∠2在两直线的同侧,并且在第三条直线(截线)的同旁,故是同位角,
而图③中,∠1与∠2是两条直线被第三条直线所截形成的同位角.
故选:B.
12.【解答】解:根据两直线平行,同位角相等得到直线a和直线b的夹角与直线b和直线PC的夹角相等.
故选:A.
13.【解答】解:∵∠EAD=∠D,∠B=∠D,
∴∠EAD=∠B,
∴AD∥BC,故①正确;
∴∠AGK=∠CKG,
∵∠CKG=∠CGK,
∴∠AGK=∠CGK,
∴GK平分∠AGC;故②正确;
延长EF交AD于P,延长CH交AD于Q,
∵EF∥CH,
∴∠EPQ=∠CQP,
∵∠EPQ=∠E+∠EAG,
∴∠CQG=∠E+∠EAG,
∵AD∥BC,
∴∠HCK+∠CQG=180°,
∴∠E+∠EAG+∠HCK=180°;故③正确;
∵∠FGA的余角比∠DGH大16°,
∴90°﹣∠FGA﹣∠DGH=16°,
∵∠FGA=∠DGH,
∴90°﹣2∠FGA=16°,
∴∠FGA=∠DGH=37°,
设∠AGM=α,∠MGK=β,
∴∠AGK=α+β,
∵GK平分∠AGC,
∴∠CGK=∠AGK=α+β,
∵GM平分∠FGC,
∴∠FGM=∠CGM,
∴∠FGA+∠AGM=∠MGK+∠CGK,
∴37°+α=β+α+β,
∴β=18.5°,
∴∠MGK=18.5°,故④错误,
故选:B.
二.填空题(共9小题)
14.【解答】解:∵三角形ABC沿射线AB方向平移3个单位至三角形EFG,
∴FG=BC=6,BF=3,△ABC≌△EFG,
∴S△ABC=S△EFG,
即S四边形AEMC+S△EBM=S△EBM+S梯形BFGM,
∴S四边形AEMC=S梯形BFGM(6﹣2+6)×3=15.
故答案为15.
15.【解答】解:由题意,空白部分是矩形,长为(a﹣2)cm,宽为(b﹣1)cm,
∴阴影部分的面积=ab×2﹣2(a﹣2)(b﹣1)=(4b+2a﹣4)cm2,
故答案为:(4b+2a﹣4).
16.【解答】解:∵△ABC中,∠A=60°,∠B=76°,
∴∠ACB=180°﹣60°﹣76°=44°.
∵CD是∠ACB的平分线,
∴∠BCD∠ACB=22°.
∵DE∥BC,
∴∠EDC=∠BCD=22°.
故答案为:22°.
17.【解答】解:由折叠性质得到,∠AEF=∠GEF=70°,
∴∠AEG=∠AEF+∠GEF=140°,
∴∠GEH=180°﹣140°=40°,
∵EG∥B′H,
∴∠EHB′=∠GEH=40°,
故答案为:40°.
18.【解答】解:由平移的性质知,AB与CE平行且相等,
∴四边形ACEB是平行四边形,BE=AC,
当B、D、E不共线时,
∵AB∥CE,∠DCE=∠AOC=60°,
∴AB=CE,AB=CD,
∴CE=CD,
∴△CED是等边三角形,
∴DE=AB,
根据三角形的三边关系知:BE+BD=AC+BD>DE=AB,
即AC+BD>AB.
当D、B、E共线时,AC+BD=AB.
故答案为:AC+BD≥AB.
19.【解答】解:∵AD∥CB,
∴∠EFC+∠DEF=180°,∠EFB=∠DEF,
即∠EFC=180°﹣72°=108°,∠EFB=72°,
∴∠BFH=108°﹣72°=36°.
∵∠H=∠D=90°,
∴∠HMF=180°﹣90°﹣36°=54°.
由折叠可得:∠NMF=∠HMF=54°,
∴∠GMN=72°.
故答案为:72.
20.【解答】解:延长OA交CD于点F,延长D'C交AB于点G,
∵CD∥OE,
∴OA⊥CD,
∵AO⊥OE,D'C⊥AB,
∴∠AGC=∠AFC=90°,
∴∠GCF+∠GAF=180°,
∵∠DCD'+∠GCF=180°,
∴∠DCD'=∠GAF,
∴∠BAO=180°﹣∠DCD',
∴∠B(180°﹣∠DCD'),
∵∠BCD﹣∠DCD'=126°,
∴∠BCD=∠DCD'+126°,
在四边形ABCF中,有∠GAF+∠B+∠BCD+∠AFC=360°,
∴∠DCD'(180°﹣∠DCD')+∠DCD'+126°+90°=360°,
解得:∠DCD'=36°,
故答案为:36°.
21.【解答】解:过点B作BG∥AM,如图:
∵BD⊥AM,
∴∠ABD+∠BAD=90°,DB⊥BG,即∠ABD+∠ABG=90°,
又∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,则
∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=3∠DBE=3α,
∴∠AFC=3α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=3α+β,
△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得
(2α+β)+3α+(3α+β)=180°,①
由AB⊥BC,可得
β+β+2α=90°,②
由①②联立方程组,解得α=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°.
故答案为:105°.
22.【解答】解:∵CD∥OB,∠EFD=α,
∴∠EOB=∠EFD=α,
∵OE平分∠AOB,
∴∠COF=∠EOB=α,故①正确;
∠AOB=2α,
∵∠AOB+∠AOH=180°,
∴∠AOH=180°﹣2α,故②正确;
∵CD∥OB,CH⊥OB,
∴CH⊥CD,故③正确;
∴∠HCO+∠HOC=90°,∠AOB+∠HOC=180°,
∴∠OCH=2α﹣90°,故④正确.
故答案为①②③④.
三.解答题(共10小题)
23.【解答】解:(1)补全施工路线如图1所示.过C作l⊥AB的延长线于G,过D作直线m⊥AB的延长线于H,
则l∥m,
根据平行线的性质可得:∠BCG=25°,∠CDH=∠GCD=70°﹣∠BCG=70°﹣25°=45°,
又∠HDE=90°,
∴∠CDE=∠CDH+∠HDE=45°+90°=135°.
(2)如图1所示,
设∠DMN=x,∠CDM=y,
由于DE∥FN,
∴∠EDM=180°﹣∠DMN=180°﹣x,
又∠CDM=y=∠CDE﹣∠EDM=135°﹣(180°﹣x)=x﹣45°,
则x﹣y=45°,
即∠DMN﹣∠CDM=45°.
24.【解答】解:(1)AD∥BF,理由如下:
∵DE∥AB,
∴∠ABC=∠BCE,
∵∠ABC=∠ADC,
∴∠BCE=∠ADC,
∴AD∥BF.
(2)∵BD平分∠ABC,
∴∠ABD=∠1∠ABC,
∵DE∥AB,
∴∠DCF=∠ABC=2∠1,
∵∠1+∠2=110°,∠DCF+∠2=180°,
∴∠1=70°,
∴∠DCF=140°.
25.【解答】解:(1)∵AD∥BE,∠E=20°,
∴∠DAE=∠E=20°,
∵∠BAE=87°,
∴∠BAD=107°,
∵AB∥CD,
∴∠ADC=73°;
(2)∵∠AFC=∠DAE+∠D=93°,
又∵∠AFB:∠BFC=1:2,
∴∠AFB=31°,
∴∠FBC=∠AFB﹣∠E=11°.
26.【解答】解:(1)ED∥AB,理由如下:
∵∠D与∠1互余,
∴∠D+∠1=90°,
∵OC⊥OD,
∴∠COD=90°,
∴∠D+∠1+∠COD=180°,
∴∠D+∠AOD=180°,
∴ED∥AB;
(2)解:∵ED∥AB,
∴∠BOF+∠OFD=180°,
∵∠OFD=70°,
∴∠BOF=110°,
∵OD平分∠BOF,
∴∠BOD∠BOF=55°,
∴∠1=180°﹣∠COD﹣∠BOD=180°﹣90°﹣55°=35°.
27.【解答】证明:∵∠BHC=∠FHD,∠GFH+∠BHC=180°,
∴∠GFH+∠FHD=180°.
∴FG∥BD.
∴∠1=∠ABD.
∵BD平分∠ABC,
∴∠2=∠ABD
∴∠1=∠2.
故答案为:∠1=∠ABD;∠2=∠ABD.
28.【解答】解:(1)①∵CD∥EF,∠ABF=60°,
∴∠ABF+∠BAD=180°.
∴∠BAD=180°﹣∠ABF=180°﹣60°=120°.
②∵当射线BN旋转到BF的位置时,两者停止运动,
∴当x=180°÷5°=36时,两者停止运动.
此时,射线AM在∠BAD的内部.
由题意知:0≤x≤36.
∵∠ABE+∠ABF=180°,
∴∠ABE=180°﹣∠ABF=180°﹣60°=120°.
当射线BN旋转到BA所在直线时,则射线BN过点A.
∴射线BN旋转的角度为120.
∴(5x)°=120°.
∴x=24(符合题意).
(2)当AM∥BN时,∠NBA=∠MAB.
∴∠EBA﹣∠EBN=∠MAB.
∴120°﹣5° x=1° x.
∴x=20(符合题意).
(3)①若P在CD与EF之间,则x>24.
由题意可得:∠EBP=(5x)°,∠BAP=(1x)°=x°,∠APB=126°.
∴∠ABP=∠EBP﹣∠EBA=(5x)°﹣120°.
又∵∠ABP+∠BAP+∠APB=180°,
∴(5x)°﹣120°+x°+126°=180°.
∴x=29(符合题意).
②如图4,当0<x<20时,∠APB=120°﹣6°x,
如图5,当20<x<24时,∠APB=6°x﹣120°.
29.【解答】解:(1)∵BD平分∠ABN,∠ABD=α,
∴∠ABD=∠DBC=α,
又∵AM∥BN,
∴∠ADB=∠DBC=α;
(2)∵BD平分∠ABN,∠ABD=α,
∴∠ABC=2∠ABD=2α,
∵AM∥BN,
∴∠ABC=∠EAF=2α,
∵GH∥BE,
∴∠BEF=∠HFE,
∵FH平分∠EFD,
∴∠EFD=2∠EFH,
又∵∠EFD=∠EAF+∠BEF,
∴2∠BEF=2α+∠BEF,
∴∠BEF=2α.
30.【解答】解:(1)∵AB∥CD,
∴∠BEF+∠EFD=180°,
∵EG平分∠BEF,FG平分∠EFD,
∴∠1∠BEF,∠2∠EFD,
∴∠1+∠2(∠BEF+∠EFD)=90°,
∵∠1=50°,
∴∠2=40°;
(2)EH∥FG,理由如下:
∵AB∥CD,
∴∠AEF=∠EFD,
∵FG平分∠EFD,EH平分∠AEF,
∴∠EFG∠EFD,∠HEF∠AEF,
∴∠EFG=∠HEF,
∴EH∥FG.
31.【解答】(1)解:∵∠ABE+∠ABD=180°,∠ABE+∠BCF=180°,
∴∠ABD=∠BCF,
∵BD是∠ABC的角平分线,∠ABC=80°,
∴∠ABD∠ABC=40°,
∴∠BCF=40°.
(2)证明:∵∠ABE+∠ABD=180°,∠ABE+∠BCF=180°,
∴∠ABD=∠BCF,
∵BD是∠ABC的角平分线,
∴∠ABD=∠DBC,
∴∠DBC=∠BCF,
∴DE∥CF.
(3)解:由(2)知,DE∥CF,
∴∠ADB=∠ACF,
∵CB是∠ACF的角平分线,
∴∠ACF=2∠BCF,
∴∠ADB=2∠BCF,
由(1)知∠ABD=∠BCF,
∴∠ADB=2∠ABD,
∵∠ADB=k∠ABD,
∴k=2.
32.【解答】解:(1)∵CD∥OE,
∴∠AOE=∠OCD=120°,
∴∠BOE=360°﹣∠AOE﹣∠AOB=360°﹣90°﹣120°=150°;
(2)∠OCD+∠BO′E′=360°﹣α.
证明:如图②,过O点作OF∥CD,
∵CD∥O′E′,
∴OF∥O′E′,
∴∠AOF=180°﹣∠OCD,∠BOF=∠E′O′O=180°﹣∠BO′E′,
∴∠AOB=∠AOF+∠BOF=180°﹣∠OCD+180°﹣∠BO′E′=360°﹣(∠OCD+∠BO′E′)=α,
∴∠OCD+∠BO′E′=360°﹣α;
(3)∠AOB=∠BO′E′.
证明:∵∠CPO′=90°,
∴PO′⊥CP,
∵PO′⊥OB,
∴CP∥OB,
∴∠PCO+∠AOB=180°,
∴2∠PCO=360°﹣2∠AOB,
∵CP是∠OCD的平分线,
∴∠OCD=2∠PCO=360°﹣2∠AOB,
∵由(2)知,∠OCD+∠BO′E′=360°﹣α=360°﹣∠AOB,
∴360°﹣2∠AOB+∠BO′E′=360°﹣∠AOB,
∴∠AOB=∠BO′E′.
一.选择题(共13小题)
1.(2021春 西湖区期末)如图,AB∥DE,BC⊥CD,则以下说法中正确的是( )
A.α,β的角度数之和为定值
B.α随β增大而增大
C.α,β的角度数之积为定值
D.α随β增大而减小
2.(2021 宁波模拟)如图,所有角均为直角,所有线段均不相等,若要知道该图形周长,至少需要知道几条线段的长( )
A.3条 B.4条 C.5条 D.6条
3.(2021春 奉化区校级期末)如图所示,直线a∥b,直线c与直线a,b分别交于点D,E,射线DF⊥直线c,若∠1=32°,则∠2的度数是( )
A.67° B.48° C.32° D.58°
4.(2021春 奉化区校级期末)下列说法正确的有( )
①两条直线被第三条直线所截,内错角相等
②平面内,过一点有且只有一条直线与已知直线垂直
③平面内,过一点有且只有一条直线与已知直线平行
④相等的角是对顶角
⑤点A为直线a外一点,点B是直线a上一点,点A到直线a的距离为5,则AB的长度不小于5
A.1个 B.2个 C.3个 D.4个
5.(2021春 奉化区校级期末)如图,已知长方形纸片ABCD,点E,H在AD边上,点F,G在BC边上,分别沿EF,GH折叠,使点B和点C都落在点P处,若∠FEH+∠EHG=118°,则∠FPG的度数为( )
A.54° B.55° C.56° D.57°
6.(2021春 奉化区校级期末)如图,在三角形ABC中,∠BAC=90°,AB=3cm,AC=4cm,把三角形ABC沿着直线BC向右平移2.5cm后得到三角形DEF,连接AE,AD,有以下结论:①AC∥DF; ②AD∥CF; ③CF=2.5cm;④DE⊥AC.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
7.(2021春 东阳市期末)如图,直线a、b被直线c所截,与∠1是同位角的( )
A.∠2 B.∠3 C.∠4 D.∠5
8.(2021春 奉化区校级期末)如图,l1∥l2∥l3,∠1,∠2,∠3如图所示,则下列各式正确的是( )
A.∠3=∠1+∠2 B.∠2+∠3﹣∠1=90°
C.∠1﹣∠2+∠3=180° D.∠2+∠3﹣∠1=180°
9.(2021春 奉化区校级期末)含30°角的直角三角板与直线a,b的位置关系如图所示,已知a∥b,∠1=35°.则∠ADC的度数是( )
A.35° B.45° C.55° D.65°
10.(2021春 奉化区校级期末)如图,在墙面上安装某一管道需经两次拐弯,拐弯后的管道与拐弯前的管道平行.若第一个弯道处∠B=142°,则第二个弯道处∠C的度数为( )
A.38° B.142° C.152° D.162°
11.(2021春 奉化区校级期末)下面图形中,∠1和∠2是同位角的是( )
A.①② B.①③ C.②③ D.②④
12.(2021春 奉化区校级期末)如图,小敏在作业中的一道题:如图1,直线a,b所成的角跑到画板外面去了,你有什么办法量出这两条直线所成的角的度数?小敏的做法是:如图2,画PC∥a,量出直线b与PC的夹角度数,即直线a,b所成角的度数.其依据是( )
A.两直线平行,同位角相等
B.同旁内角互补,两直线平行
C.内错角相等,两直线平行
D.同位角相等,两直线平行
13.(2021春 奉化区校级期末)如图,E在线段BA的延长线上,∠EAD=∠D,∠B=∠D,EF∥HC,连FH交AD于G,∠FGA的余角比∠DGH大16°,K为线段BC上一点,连CG,使∠CKG=∠CGK,在∠AGK内部有射线GM,GM平分∠FGC,则下列结论:①AD∥BC;②GK平分∠AGC;③∠E+∠EAG+∠HCK=180°;④∠MGK的角度为定值且定值为16°,其中正确结论的个数有( )
A.4个 B.3个 C.2个 D.1个
二.填空题(共9小题)
14.(2021春 慈溪市期末)如图,在三角形ABC中,BC=6,把三角形ABC沿射线AB方向平移3个单位至三角形EFG处,EG与BC交于点M.若CM=2,则图中阴影部分的面积为 .
15.(2021春 萧山区期末)如图,将长为acm(a>2),宽为bcm(b>1)的长方形ABCD先向右平移2cm,再向下平移1cm,得到长方形A′B′C′D′,则阴影部分的面积为 cm2.(用含a、b的代数式表示,结果要求化成最简)
16.(2021春 镇海区校级期末)如图,已知DE∥BC,CD是∠ACB的平分线,∠A=60°,∠B=76°,则∠EDC的度数为 .
17.(2021春 西湖区期末)如图①,将长方形纸带沿EF折叠,∠AEF=70°,再沿GH折叠成图②,则图②中∠EHB'= .
18.(2021春 奉化区校级期末)如图,线段AB=CD,AB与CD相交于点O,且∠AOC=60°,CE是由AB平移所得,则AC+BD与AB的大小关系是 .
19.(2021春 滨江区校级期末)如图a,已知长方形纸带ABCD,将纸带沿EF折叠后,点C、D分别落在H、G的位置,再沿BC折叠成图b,若∠DEF=72°,则∠GMN= °.
20.(2021春 奉化区校级期末)图1是一盏可折叠台灯.图2为其平面示意图,底座AO⊥OE于点O,支架AB,BC为固定支撑杆,∠A是∠B的两倍,灯体CD可绕点C旋转调节.现把灯体CD从水平位置旋转到CD′位置(如图2中虚线所示),此时,灯体CD′所在的直线恰好垂直支架AB,且∠BCD﹣∠DCD′=126°,则∠DCD′= .
21.(2021春 奉化区校级期末)如图,已知AM∥CN,点B为平面内一点,AB⊥BC于B,过点B作BD⊥AM于点D,点E、F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,则∠EBC的度数为 .
22.(2021春 奉化区校级期末)如图,C为∠AOB的边OA上一点,过点C作CD∥OB交∠AOB的平分线OE于点F,作CH⊥OB交BO的延长线于点H,若∠EFD=α,现有以下结论:①∠COF=α;②∠AOH=180°﹣2α;③CH⊥CD;④∠OCH=2α﹣90°.其中正确的是 (填序号).
三.解答题(共10小题)
23.(2021春 上城区期末)如图,政府规划由西向东修一条公路.从A修至B后为了绕开村庄,改为沿南偏东25°方向修建BC段,在C处又改变方向修建CD段,测得∠BCD=70°,在D处继续改变方向,朝与出发时相同的方向修至E.
(1)补全施工路线示意图,求∠CDE的度数;
(2)原计划在AB的延长线上依次修建两个公交站M,N(均在CD右侧),连结DM和MN,求∠CDM与∠DMN的数量关系.
24.(2021春 乐清市期末)如图,BF交DE于点C,DE∥AB,∠ABC=∠ADC.
(1)AD与BF平行吗?请说明理由.
(2)若BD平分∠ABC,且∠1+∠2=110°,求∠DCF的度数.
25.(2021春 浦江县期末)如图,已知AB∥CD,AD∥BE,点C在线段BE上,∠BAE=87°,∠E=20°,AE与CD交于点F.
(1)求∠ADC的度数;
(2)连结BF,若∠AFB:∠BFC=1:2,求∠FBC的度数.
26.(2021春 北仑区期末)如图,点O在直线AB上,OC⊥OD,∠D与∠1互余,F是DE上一点,连接OF.
(1)ED是否平行于AB,请说明理由;
(2)若OD平分∠BOF,∠OFD=70°,求∠1的度数.
27.(2021春 椒江区期末)如图:BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H.∠GFH+∠BHC=180°,求证:∠1=∠2.
证明:∵∠BHC=∠FHD,∠GFH+∠BHC=180°,
∴∠GFH+∠FHD=180°
∴FG平行BD
∴
∵BD平分∠ABC,
∴
∴∠1=∠2
28.(2021春 慈溪市期末)如图,直线CD∥EF,点A,B分别在直线CD,EF上(自左至右分别为C,A,D和E,B,F),∠ABF=60°.射线AM自射线AB的位置开始,绕点A以每秒1°的速度沿逆时针方向旋转,同时,射线BN自射线BE开始以每秒5°的速度绕点B沿顺时针方向旋转,当射线BN旋转到BF的位置时,两者停止运动.设旋转时间为x秒.
(1)如图1,直接写出下列答案:
①∠BAD的度数;
②射线BN过点A时的x的值.
(2)如图2,求当AM∥BN时的x的值.
(3)若两条射线AM和BN所在的直线交于点P.
①如图3,若P在CD与EF之间,且∠APB=126°,求x的值.
②若x<24,求∠APB的度数(直接写出用含x的代数式表示的结果).
29.(2021春 江干区期末)已知AM∥BN,BD平分∠ABN交AM于点D,E为射线BA上的点,连接ED交BN于C,设∠ABD=α.
(1)如图1,求∠ADB的度数(用α表示);
(2)如图2,若F为AD上的点,∠EFD的平分线所在直线分别交BD、ED于点G、H,当HG∥BE时,求∠BEF的度数(用α表示).
30.(2021春 拱墅区期末)如图,已知AB∥CD,EG平分∠BEF,FG平分∠EFD.
(1)若∠1=50°,求∠2的度数;
(2)若EH平分∠AEF,判断EH,FG是否平行,并说明理由.
31.(2021春 拱墅区期末)如图,BD是∠ABC的角平分线,∠ABE+∠BCF=180°.
(1)若∠ABC=80°,求∠BCF的值;
(2)求证:DE∥CF;
(3)若CB是∠ACF的角平分线,∠ADB=k∠ABD,求k的值.
32.(2021春 西湖区期末)已知点C在射线OA上.
(1)如图①,CD∥OE,若∠AOB=90°,∠OCD=120°,求∠BOE的度数;
(2)在①中,将射线OE沿射线OB平移得O′E'(如图②),若∠AOB=α,探究∠OCD与∠BO′E′的关系(用含α的代数式表示);
(3)在②中,过点O′作OB的垂线,与∠OCD的平分线交于点P(如图③),若∠CPO′=90°,探究∠AOB与∠BO′E′的关系.
2022年浙江省七年级下册数学期末考试专题练-第1章《平行线》(2)
参考答案与试题解析
一.选择题(共13小题)
1.【解答】解:过C点作MF∥AB,
∵AB∥DE,
∴MF∥DE,
∴∠α=∠BCM,∠β+∠DCM=180°,
∵BC⊥CD,
∴∠BCD=90°,
∴∠BCM+∠DCM=360°﹣∠BCD=270°,
∴∠α+(180°﹣∠β)=270°,
∴∠α﹣∠β=90°,
∴α随β增大而增大,
故选:B.
2.【解答】解:如图:
若要知道该图形周长,至少需要知道4条线段的长:BC、AB,IJ,EF,
∵BC=AL+KJ+IH+GF+DE,AB=LK+KK′=LK+CC′,IJ=HG+GG′=HG+C′D′,EF=DD′,
∴只要知道BC、AB,IJ,EF4条线段的长,就能知道该图形周长.
故选:B.
3.【解答】解:
∵a∥b,
∴∠2=∠3,
∵DF⊥直线c,
∴∠FDE=∠1+∠3=90°,
∵∠1=32°,
∴∠3=90°﹣32°=58°,
∴∠2=58°.
故选:D.
4.【解答】解:①两直线不一定平行,故错误;
②平行公理,故正确;
③必须是过直线外一点,故错误;
④相等的角不一定是对顶角,故错误;
⑤垂线段最短,故正确.
故选:B.
5.【解答】解:∵四边形ABCD是长方形,
∴AD∥BC,
∴∠FEH=∠BFE,∠EHG=∠CGH,
∴∠BFE+∠CGH=∠FEH+∠EHG=118°,
由折叠可知:
EF,GH分别是∠BFP和∠CGP的角平分线,
∴∠PFE=∠BFE,∠PGH=∠CGH,
∴∠PFE+∠PGH=∠BFE+∠CGH=118°,
∴∠BFP+∠CGP=2(∠BFE+∠CGH)=236°,
∴∠PFG+∠PGF=360°﹣(∠BFP+∠CGP)=360°﹣236°=124°,
∴∠FPG=180°﹣(∠PFG+∠PGF)=180°﹣124°=56°.
故选:C.
6.【解答】解:∵△ABC沿着直线BC的方向平移2.5cm后得到△DEF,
∴AC∥DF,故①正确;
AD∥CF,故②正确;
CF=AD=2.5cm,故③正确;
AB∥DE,
又∵∠BAC=90°,
∴BA⊥AC,
∴DE⊥AC,故④正确;
故选:D.
7.【解答】解:A、∠2与∠1是同位角,故本选项符合题意;
B、∠3与∠1不是同位角,故本选项不符合题意;
C、∠4与∠1是同位角,故本选项不符合题意;
D、∠5与∠1不是同位角,故本选项不符合题意;
故选:A.
8.【解答】解:∵l1∥l2∥l3,
∴∠1=∠2+∠4,∠4+∠3=180°,
∴∠1﹣∠2+∠3=180°,
故选:C.
9.【解答】解:∵a∥b,
∴∠BDC=∠1=35°.
又∵∠ADB=90°,
∴∠ADC=90°﹣35°=55°.
故选:C.
10.【解答】解:如图所示:
∵拐弯后的管道与拐弯前的管道平行,
∴AB∥CD,
∴∠B=∠C,
又∵∠B=142°,
∴∠C=142°,
故选:B.
11.【解答】解:根据同位角的定义,可得图①中,∠1与∠2在两直线的同侧,并且在第三条直线(截线)的同旁,故是同位角,
而图③中,∠1与∠2是两条直线被第三条直线所截形成的同位角.
故选:B.
12.【解答】解:根据两直线平行,同位角相等得到直线a和直线b的夹角与直线b和直线PC的夹角相等.
故选:A.
13.【解答】解:∵∠EAD=∠D,∠B=∠D,
∴∠EAD=∠B,
∴AD∥BC,故①正确;
∴∠AGK=∠CKG,
∵∠CKG=∠CGK,
∴∠AGK=∠CGK,
∴GK平分∠AGC;故②正确;
延长EF交AD于P,延长CH交AD于Q,
∵EF∥CH,
∴∠EPQ=∠CQP,
∵∠EPQ=∠E+∠EAG,
∴∠CQG=∠E+∠EAG,
∵AD∥BC,
∴∠HCK+∠CQG=180°,
∴∠E+∠EAG+∠HCK=180°;故③正确;
∵∠FGA的余角比∠DGH大16°,
∴90°﹣∠FGA﹣∠DGH=16°,
∵∠FGA=∠DGH,
∴90°﹣2∠FGA=16°,
∴∠FGA=∠DGH=37°,
设∠AGM=α,∠MGK=β,
∴∠AGK=α+β,
∵GK平分∠AGC,
∴∠CGK=∠AGK=α+β,
∵GM平分∠FGC,
∴∠FGM=∠CGM,
∴∠FGA+∠AGM=∠MGK+∠CGK,
∴37°+α=β+α+β,
∴β=18.5°,
∴∠MGK=18.5°,故④错误,
故选:B.
二.填空题(共9小题)
14.【解答】解:∵三角形ABC沿射线AB方向平移3个单位至三角形EFG,
∴FG=BC=6,BF=3,△ABC≌△EFG,
∴S△ABC=S△EFG,
即S四边形AEMC+S△EBM=S△EBM+S梯形BFGM,
∴S四边形AEMC=S梯形BFGM(6﹣2+6)×3=15.
故答案为15.
15.【解答】解:由题意,空白部分是矩形,长为(a﹣2)cm,宽为(b﹣1)cm,
∴阴影部分的面积=ab×2﹣2(a﹣2)(b﹣1)=(4b+2a﹣4)cm2,
故答案为:(4b+2a﹣4).
16.【解答】解:∵△ABC中,∠A=60°,∠B=76°,
∴∠ACB=180°﹣60°﹣76°=44°.
∵CD是∠ACB的平分线,
∴∠BCD∠ACB=22°.
∵DE∥BC,
∴∠EDC=∠BCD=22°.
故答案为:22°.
17.【解答】解:由折叠性质得到,∠AEF=∠GEF=70°,
∴∠AEG=∠AEF+∠GEF=140°,
∴∠GEH=180°﹣140°=40°,
∵EG∥B′H,
∴∠EHB′=∠GEH=40°,
故答案为:40°.
18.【解答】解:由平移的性质知,AB与CE平行且相等,
∴四边形ACEB是平行四边形,BE=AC,
当B、D、E不共线时,
∵AB∥CE,∠DCE=∠AOC=60°,
∴AB=CE,AB=CD,
∴CE=CD,
∴△CED是等边三角形,
∴DE=AB,
根据三角形的三边关系知:BE+BD=AC+BD>DE=AB,
即AC+BD>AB.
当D、B、E共线时,AC+BD=AB.
故答案为:AC+BD≥AB.
19.【解答】解:∵AD∥CB,
∴∠EFC+∠DEF=180°,∠EFB=∠DEF,
即∠EFC=180°﹣72°=108°,∠EFB=72°,
∴∠BFH=108°﹣72°=36°.
∵∠H=∠D=90°,
∴∠HMF=180°﹣90°﹣36°=54°.
由折叠可得:∠NMF=∠HMF=54°,
∴∠GMN=72°.
故答案为:72.
20.【解答】解:延长OA交CD于点F,延长D'C交AB于点G,
∵CD∥OE,
∴OA⊥CD,
∵AO⊥OE,D'C⊥AB,
∴∠AGC=∠AFC=90°,
∴∠GCF+∠GAF=180°,
∵∠DCD'+∠GCF=180°,
∴∠DCD'=∠GAF,
∴∠BAO=180°﹣∠DCD',
∴∠B(180°﹣∠DCD'),
∵∠BCD﹣∠DCD'=126°,
∴∠BCD=∠DCD'+126°,
在四边形ABCF中,有∠GAF+∠B+∠BCD+∠AFC=360°,
∴∠DCD'(180°﹣∠DCD')+∠DCD'+126°+90°=360°,
解得:∠DCD'=36°,
故答案为:36°.
21.【解答】解:过点B作BG∥AM,如图:
∵BD⊥AM,
∴∠ABD+∠BAD=90°,DB⊥BG,即∠ABD+∠ABG=90°,
又∵AB⊥BC,
∴∠CBG+∠ABG=90°,
∴∠ABD=∠CBG,
∵BF平分∠DBC,BE平分∠ABD,
∴∠DBF=∠CBF,∠DBE=∠ABE,
∴∠ABF=∠GBF,
设∠DBE=α,∠ABF=β,则
∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC=3∠DBE=3α,
∴∠AFC=3α+β,
∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,
∴∠FCB=∠AFC=3α+β,
△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得
(2α+β)+3α+(3α+β)=180°,①
由AB⊥BC,可得
β+β+2α=90°,②
由①②联立方程组,解得α=15°,
∴∠ABE=15°,
∴∠EBC=∠ABE+∠ABC=15°+90°=105°.
故答案为:105°.
22.【解答】解:∵CD∥OB,∠EFD=α,
∴∠EOB=∠EFD=α,
∵OE平分∠AOB,
∴∠COF=∠EOB=α,故①正确;
∠AOB=2α,
∵∠AOB+∠AOH=180°,
∴∠AOH=180°﹣2α,故②正确;
∵CD∥OB,CH⊥OB,
∴CH⊥CD,故③正确;
∴∠HCO+∠HOC=90°,∠AOB+∠HOC=180°,
∴∠OCH=2α﹣90°,故④正确.
故答案为①②③④.
三.解答题(共10小题)
23.【解答】解:(1)补全施工路线如图1所示.过C作l⊥AB的延长线于G,过D作直线m⊥AB的延长线于H,
则l∥m,
根据平行线的性质可得:∠BCG=25°,∠CDH=∠GCD=70°﹣∠BCG=70°﹣25°=45°,
又∠HDE=90°,
∴∠CDE=∠CDH+∠HDE=45°+90°=135°.
(2)如图1所示,
设∠DMN=x,∠CDM=y,
由于DE∥FN,
∴∠EDM=180°﹣∠DMN=180°﹣x,
又∠CDM=y=∠CDE﹣∠EDM=135°﹣(180°﹣x)=x﹣45°,
则x﹣y=45°,
即∠DMN﹣∠CDM=45°.
24.【解答】解:(1)AD∥BF,理由如下:
∵DE∥AB,
∴∠ABC=∠BCE,
∵∠ABC=∠ADC,
∴∠BCE=∠ADC,
∴AD∥BF.
(2)∵BD平分∠ABC,
∴∠ABD=∠1∠ABC,
∵DE∥AB,
∴∠DCF=∠ABC=2∠1,
∵∠1+∠2=110°,∠DCF+∠2=180°,
∴∠1=70°,
∴∠DCF=140°.
25.【解答】解:(1)∵AD∥BE,∠E=20°,
∴∠DAE=∠E=20°,
∵∠BAE=87°,
∴∠BAD=107°,
∵AB∥CD,
∴∠ADC=73°;
(2)∵∠AFC=∠DAE+∠D=93°,
又∵∠AFB:∠BFC=1:2,
∴∠AFB=31°,
∴∠FBC=∠AFB﹣∠E=11°.
26.【解答】解:(1)ED∥AB,理由如下:
∵∠D与∠1互余,
∴∠D+∠1=90°,
∵OC⊥OD,
∴∠COD=90°,
∴∠D+∠1+∠COD=180°,
∴∠D+∠AOD=180°,
∴ED∥AB;
(2)解:∵ED∥AB,
∴∠BOF+∠OFD=180°,
∵∠OFD=70°,
∴∠BOF=110°,
∵OD平分∠BOF,
∴∠BOD∠BOF=55°,
∴∠1=180°﹣∠COD﹣∠BOD=180°﹣90°﹣55°=35°.
27.【解答】证明:∵∠BHC=∠FHD,∠GFH+∠BHC=180°,
∴∠GFH+∠FHD=180°.
∴FG∥BD.
∴∠1=∠ABD.
∵BD平分∠ABC,
∴∠2=∠ABD
∴∠1=∠2.
故答案为:∠1=∠ABD;∠2=∠ABD.
28.【解答】解:(1)①∵CD∥EF,∠ABF=60°,
∴∠ABF+∠BAD=180°.
∴∠BAD=180°﹣∠ABF=180°﹣60°=120°.
②∵当射线BN旋转到BF的位置时,两者停止运动,
∴当x=180°÷5°=36时,两者停止运动.
此时,射线AM在∠BAD的内部.
由题意知:0≤x≤36.
∵∠ABE+∠ABF=180°,
∴∠ABE=180°﹣∠ABF=180°﹣60°=120°.
当射线BN旋转到BA所在直线时,则射线BN过点A.
∴射线BN旋转的角度为120.
∴(5x)°=120°.
∴x=24(符合题意).
(2)当AM∥BN时,∠NBA=∠MAB.
∴∠EBA﹣∠EBN=∠MAB.
∴120°﹣5° x=1° x.
∴x=20(符合题意).
(3)①若P在CD与EF之间,则x>24.
由题意可得:∠EBP=(5x)°,∠BAP=(1x)°=x°,∠APB=126°.
∴∠ABP=∠EBP﹣∠EBA=(5x)°﹣120°.
又∵∠ABP+∠BAP+∠APB=180°,
∴(5x)°﹣120°+x°+126°=180°.
∴x=29(符合题意).
②如图4,当0<x<20时,∠APB=120°﹣6°x,
如图5,当20<x<24时,∠APB=6°x﹣120°.
29.【解答】解:(1)∵BD平分∠ABN,∠ABD=α,
∴∠ABD=∠DBC=α,
又∵AM∥BN,
∴∠ADB=∠DBC=α;
(2)∵BD平分∠ABN,∠ABD=α,
∴∠ABC=2∠ABD=2α,
∵AM∥BN,
∴∠ABC=∠EAF=2α,
∵GH∥BE,
∴∠BEF=∠HFE,
∵FH平分∠EFD,
∴∠EFD=2∠EFH,
又∵∠EFD=∠EAF+∠BEF,
∴2∠BEF=2α+∠BEF,
∴∠BEF=2α.
30.【解答】解:(1)∵AB∥CD,
∴∠BEF+∠EFD=180°,
∵EG平分∠BEF,FG平分∠EFD,
∴∠1∠BEF,∠2∠EFD,
∴∠1+∠2(∠BEF+∠EFD)=90°,
∵∠1=50°,
∴∠2=40°;
(2)EH∥FG,理由如下:
∵AB∥CD,
∴∠AEF=∠EFD,
∵FG平分∠EFD,EH平分∠AEF,
∴∠EFG∠EFD,∠HEF∠AEF,
∴∠EFG=∠HEF,
∴EH∥FG.
31.【解答】(1)解:∵∠ABE+∠ABD=180°,∠ABE+∠BCF=180°,
∴∠ABD=∠BCF,
∵BD是∠ABC的角平分线,∠ABC=80°,
∴∠ABD∠ABC=40°,
∴∠BCF=40°.
(2)证明:∵∠ABE+∠ABD=180°,∠ABE+∠BCF=180°,
∴∠ABD=∠BCF,
∵BD是∠ABC的角平分线,
∴∠ABD=∠DBC,
∴∠DBC=∠BCF,
∴DE∥CF.
(3)解:由(2)知,DE∥CF,
∴∠ADB=∠ACF,
∵CB是∠ACF的角平分线,
∴∠ACF=2∠BCF,
∴∠ADB=2∠BCF,
由(1)知∠ABD=∠BCF,
∴∠ADB=2∠ABD,
∵∠ADB=k∠ABD,
∴k=2.
32.【解答】解:(1)∵CD∥OE,
∴∠AOE=∠OCD=120°,
∴∠BOE=360°﹣∠AOE﹣∠AOB=360°﹣90°﹣120°=150°;
(2)∠OCD+∠BO′E′=360°﹣α.
证明:如图②,过O点作OF∥CD,
∵CD∥O′E′,
∴OF∥O′E′,
∴∠AOF=180°﹣∠OCD,∠BOF=∠E′O′O=180°﹣∠BO′E′,
∴∠AOB=∠AOF+∠BOF=180°﹣∠OCD+180°﹣∠BO′E′=360°﹣(∠OCD+∠BO′E′)=α,
∴∠OCD+∠BO′E′=360°﹣α;
(3)∠AOB=∠BO′E′.
证明:∵∠CPO′=90°,
∴PO′⊥CP,
∵PO′⊥OB,
∴CP∥OB,
∴∠PCO+∠AOB=180°,
∴2∠PCO=360°﹣2∠AOB,
∵CP是∠OCD的平分线,
∴∠OCD=2∠PCO=360°﹣2∠AOB,
∵由(2)知,∠OCD+∠BO′E′=360°﹣α=360°﹣∠AOB,
∴360°﹣2∠AOB+∠BO′E′=360°﹣∠AOB,
∴∠AOB=∠BO′E′.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
