浙教版数学七年级下册 1.3 平行线的判定 课件(共14张PPT)
文档属性
| 名称 | 浙教版数学七年级下册 1.3 平行线的判定 课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 862.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-31 11:02:21 | ||
图片预览


文档简介
(共14张PPT)
如图是木工师傅的角尺,用角尺可以很容易地画平行线,你知道这是为什么吗?
旧知再现
一
1.3 平行线的判定(2)
第 1 章
平行线
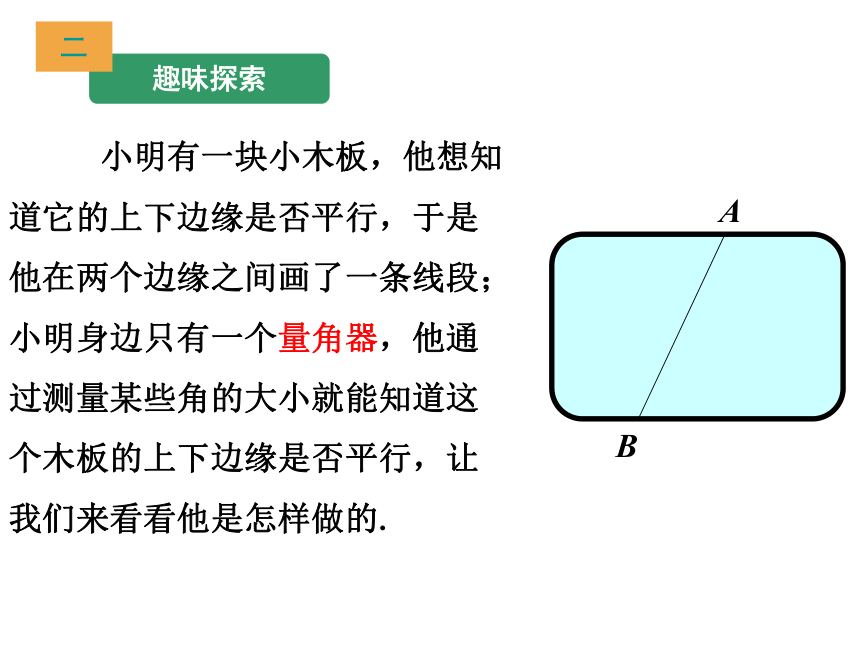
小明有一块小木板,他想知道它的上下边缘是否平行,于是他在两个边缘之间画了一条线段;小明身边只有一个量角器,他通过测量某些角的大小就能知道这个木板的上下边缘是否平行,让我们来看看他是怎样做的.
A
B
趣味探索
二
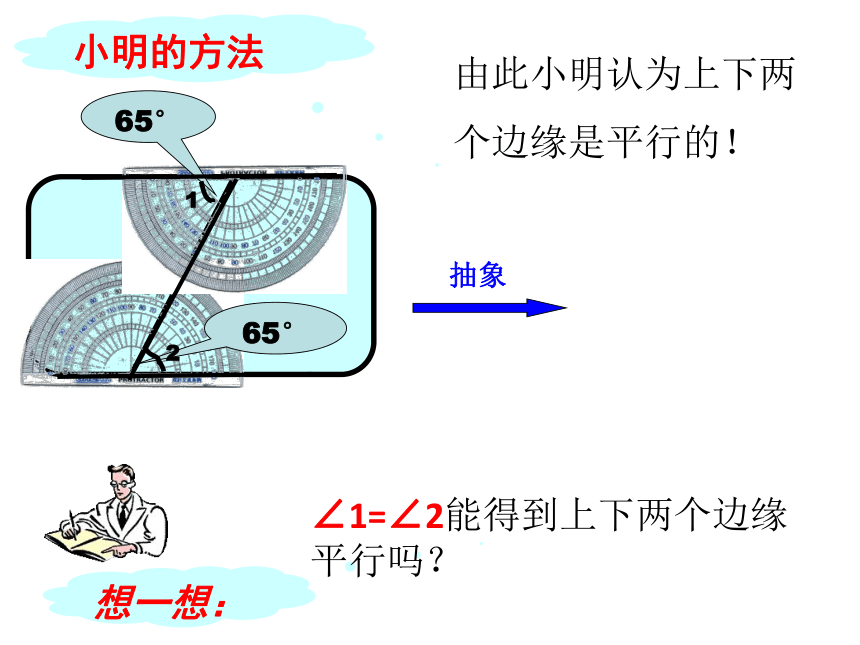
由此小明认为上下两个边缘是平行的!
65°
1
65°
2
想一想:
∠1=∠2能得到上下两个边缘平行吗?
小明的方法
抽象
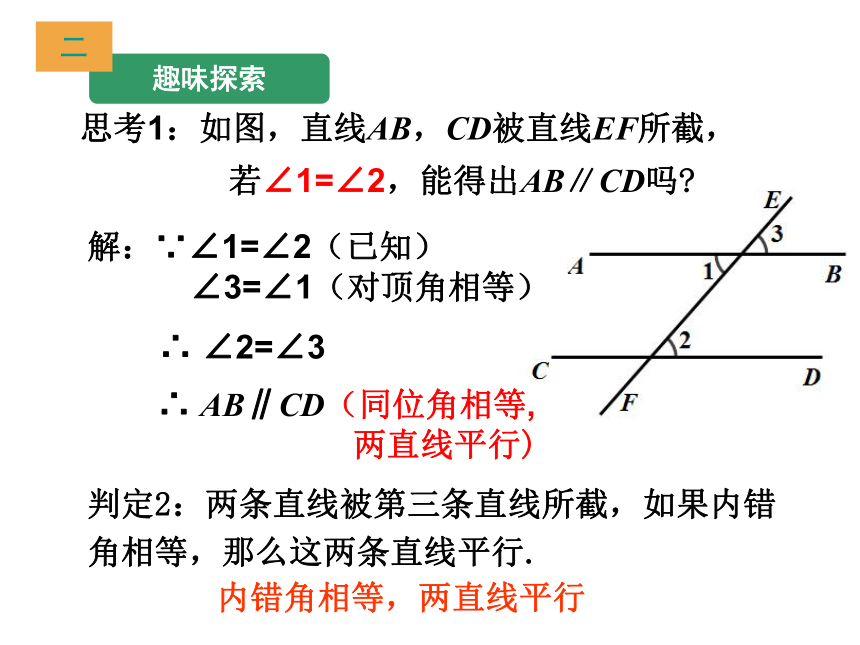
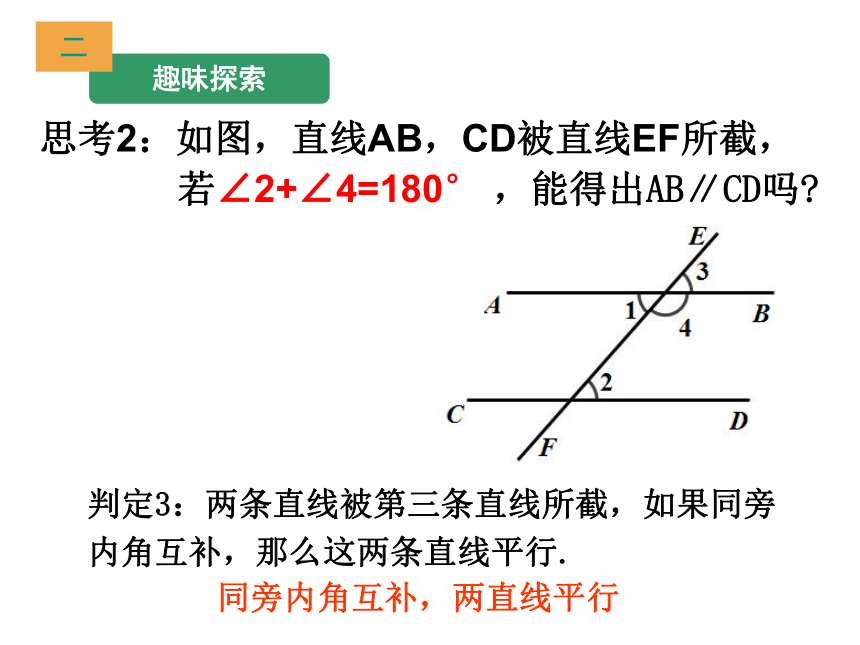
思考1:如图,直线AB,CD被直线EF所截,
若∠1=∠2,能得出AB∥CD吗
解:∵∠1=∠2(已知)
∠3=∠1(对顶角相等)
∴ ∠2=∠3
∴ AB∥CD(同位角相等,
两直线平行)
判定2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
内错角相等,两直线平行
趣味探索
二
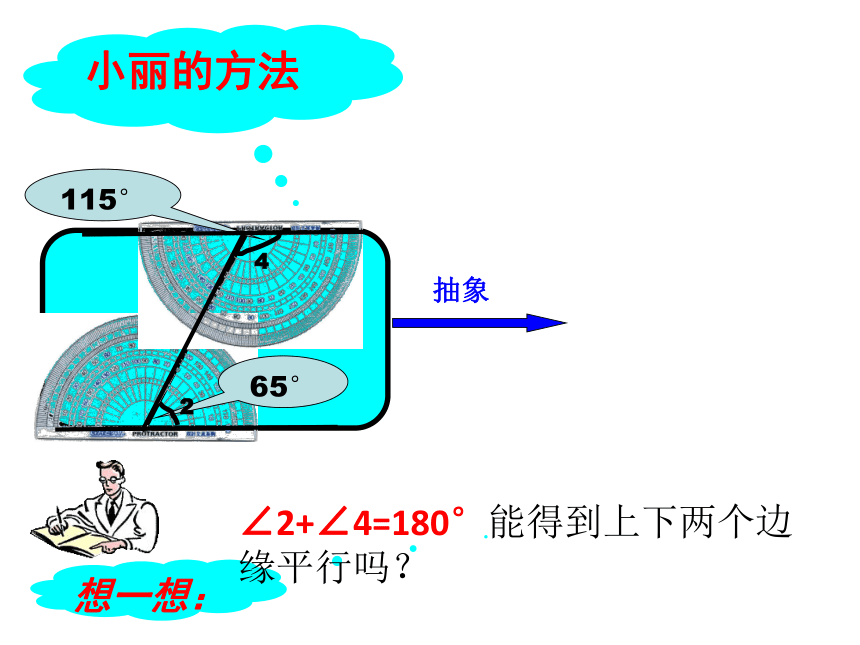
65°
2
115°
4
小丽的方法
想一想:
抽象
∠2+∠4=180°能得到上下两个边缘平行吗?
思考2:如图,直线AB,CD被直线EF所截,
若∠2+∠4=180° ,能得出AB∥CD吗
趣味探索
二
判定3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
同旁内角互补,两直线平行
判定2:内错角相等,两直线平行;
判定3:同旁内角互补,两直线平行.
判定2 ∵∠1=∠2,
∴AB∥CD.
判定3∵∠2+∠4=180°,
∴AB∥CD.
几何语言
整理归纳
三
练习1.如图,
(1)从∠1=∠2,可以推出 ∥ ,
理由是
(2)从∠2=∠ ,可以推出c∥d ,
理由是
(3)如果∠4=75°,∠3=75°,
可以推出 ∥
(4) 从∠4=75°,∠5= °,
可以推出a∥b.
b
a
内错角相等,两直线平行
同位角相等,两直线平行.
3
c
d
105
新知巩固
四
A
B
C
D
E
练习2 把相同的三角尺拼成如下的图形,
找出图中的平行的直线,并说明理由.
新知巩固
四
例1 如图,AC⊥CD于点C, ∠1与∠2互余.判断AB,CD是否平行,并说明理由.
解 AB // CD . 理由如下:
∵ AB⊥CD ,
∴ ∠2+∠3=90°.
∴ AB // CD.
C
D
A
1
B
2
∵ ∠1与∠2互余,
∴ ∠1+∠2=90°.
∴ ∠1 =∠3.
3
例题解析
五
例2 如图,AP平分∠BAC,CP平分∠ACD,
∠1+∠2=90°.判断AB,CD是否平行,并
说明理由.
P
A
C
B
D
1
2
例题解析
五
如图,如果要判定AB∥CD,只需要一个什么条件?(尽可能地把答案都写出来)
学以致用
六
感悟提升
七
平行线的判定
条件:角的关系
结论:两直线平行
思
想
方
法
建模思想
转化思想
分类思想
解
题
策
略
由因导果
执果索因
双
管
齐
下
平行线的判定
平行线的性质
如图是木工师傅的角尺,用角尺可以很容易地画平行线,你知道这是为什么吗?
旧知再现
一
1.3 平行线的判定(2)
第 1 章
平行线
小明有一块小木板,他想知道它的上下边缘是否平行,于是他在两个边缘之间画了一条线段;小明身边只有一个量角器,他通过测量某些角的大小就能知道这个木板的上下边缘是否平行,让我们来看看他是怎样做的.
A
B
趣味探索
二
由此小明认为上下两个边缘是平行的!
65°
1
65°
2
想一想:
∠1=∠2能得到上下两个边缘平行吗?
小明的方法
抽象
思考1:如图,直线AB,CD被直线EF所截,
若∠1=∠2,能得出AB∥CD吗
解:∵∠1=∠2(已知)
∠3=∠1(对顶角相等)
∴ ∠2=∠3
∴ AB∥CD(同位角相等,
两直线平行)
判定2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
内错角相等,两直线平行
趣味探索
二
65°
2
115°
4
小丽的方法
想一想:
抽象
∠2+∠4=180°能得到上下两个边缘平行吗?
思考2:如图,直线AB,CD被直线EF所截,
若∠2+∠4=180° ,能得出AB∥CD吗
趣味探索
二
判定3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
同旁内角互补,两直线平行
判定2:内错角相等,两直线平行;
判定3:同旁内角互补,两直线平行.
判定2 ∵∠1=∠2,
∴AB∥CD.
判定3∵∠2+∠4=180°,
∴AB∥CD.
几何语言
整理归纳
三
练习1.如图,
(1)从∠1=∠2,可以推出 ∥ ,
理由是
(2)从∠2=∠ ,可以推出c∥d ,
理由是
(3)如果∠4=75°,∠3=75°,
可以推出 ∥
(4) 从∠4=75°,∠5= °,
可以推出a∥b.
b
a
内错角相等,两直线平行
同位角相等,两直线平行.
3
c
d
105
新知巩固
四
A
B
C
D
E
练习2 把相同的三角尺拼成如下的图形,
找出图中的平行的直线,并说明理由.
新知巩固
四
例1 如图,AC⊥CD于点C, ∠1与∠2互余.判断AB,CD是否平行,并说明理由.
解 AB // CD . 理由如下:
∵ AB⊥CD ,
∴ ∠2+∠3=90°.
∴ AB // CD.
C
D
A
1
B
2
∵ ∠1与∠2互余,
∴ ∠1+∠2=90°.
∴ ∠1 =∠3.
3
例题解析
五
例2 如图,AP平分∠BAC,CP平分∠ACD,
∠1+∠2=90°.判断AB,CD是否平行,并
说明理由.
P
A
C
B
D
1
2
例题解析
五
如图,如果要判定AB∥CD,只需要一个什么条件?(尽可能地把答案都写出来)
学以致用
六
感悟提升
七
平行线的判定
条件:角的关系
结论:两直线平行
思
想
方
法
建模思想
转化思想
分类思想
解
题
策
略
由因导果
执果索因
双
管
齐
下
平行线的判定
平行线的性质
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
