浙教版数学七年级下册 1.4 平行线的性质(1) 教案
文档属性
| 名称 | 浙教版数学七年级下册 1.4 平行线的性质(1) 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 113.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 08:29:30 | ||
图片预览

文档简介
小翻折,大智慧
——平行线的性质与判定的复习
一、教材分析
《平行线的性质与判定的复习》,是浙教版七年级下册第一章《平行线》学习后续的复习部分。复习的主要内容是平行线的性质和判定. 本节课以翻折问题为载体,是平行线性质和判定的回顾和延伸. 本节课的学习对学生简单几何问题的推理能力和图形迁移能力的培养起着重要作用.
教学目标
知识技能:掌握平行线的判定和性质;
过程方法:经历动手折叠发现角的数量关系过程,渗透化归思想和方程思想,并逐步掌握几何说理的基本方法;
问题解决:经历添加不同条件判定平行线的过程,培养和发展逻辑思维能力和推理论证的表达能力,培养发现问题、分析问题、提出问题、解决问题的能力;
情感态度:经历性质定理、判定定理选择的过程,感受数学思考过程中的合理性、数学证明的严谨性. 认识到事物间的相互关系、相互转化,学会用辩证的观点分析事物.
三、教学重难点
项目 教学重点 教学难点
内容 平行线的性质与判定 在翻折问题中判定平行线与求角
依据 教材编排以及本课的教学目标 学生的认知特点
四、教法学法
教法:
这节课主要将“启发式”与“探究式”相结合进行教学.围绕本节课知识,引导学生经历从动手折叠直观感知,到逻辑推理证明的过程,学生积极参与,培养提出问题、分析问题、解决问题的能力.
学法:
让每一个学生积极参与课堂的知识构建,通过“自主探究”、“合作交流”等方式,由“学会”变成“会学”和“乐学”,主动经历数学知识形成的过程.
五、教学过程
环节一 激活旧知,引入课题
引 入:刚才,同学们拿到了一张长方形纸条,你能说一说它的图形特征吗?
预 设:①两组对边分别平行;
②四个角都是直角.
引 入:今天,我们就要借助这张长方形纸条,来复习平行线的相关知识.
环节二 动手操作,复习定理
【活动一】回忆平行线的性质与判定定理.
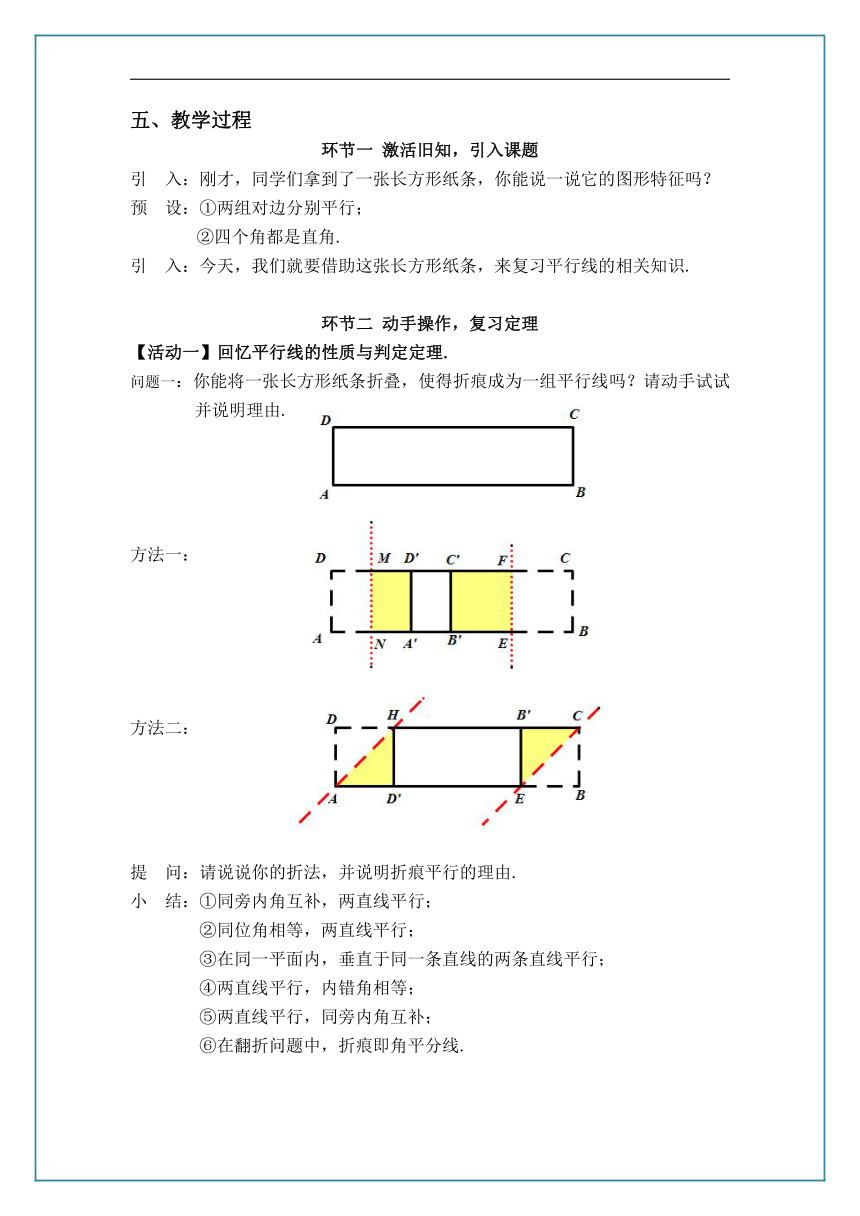
问题一:你能将一张长方形纸条折叠,使得折痕成为一组平行线吗?请动手试试并说明理由.
方法一:
方法二:
提 问:请说说你的折法,并说明折痕平行的理由.
小 结:①同旁内角互补,两直线平行;
②同位角相等,两直线平行;
③在同一平面内,垂直于同一条直线的两条直线平行;
④两直线平行,内错角相等;
⑤两直线平行,同旁内角互补;
⑥在翻折问题中,折痕即角平分线.
方法三:
提 问: 前两种折法折出了45°,90°这些特殊的角。方法三更具有一般性。是如何折出的?请你用几何语言说明折痕平行的理由.
【活动二】利用平行线的性质和判定定理进行几何说理
如图所示,将长方形纸带沿EF、GH折叠,使得DH与BE重合. 折痕GH与EF平行吗?请说明理由.
小 结:①解决翻折问题时,要先还原图形。再分清折痕平分的是哪些角。
②内错角相等,两直线平行;
③两直线平行,同位角相等。
(设计意图:在这个具有开放性的问题中,不同层次的学生可以想出不同难度的折法. 在翻折的过程中,学生从具体的动手操作中抽象出平行线的基本图形,最后进行严密的逻辑推理. )
环节三 独立思考,灵活运用
【活动一】平行的性质的运用
如图所示,将长方形纸条沿EF、GH折叠,使得DH与BE重合.
(1)若∠ =150°,求∠ 的度数.
提 问:由翻折得到哪些隐含条件?
预 设:利用平行的性质求角,会根据已知条件选择合适的方法.
(2)沿HF折叠,点B,C分别落在 , 处.∠HEF试探究α与β
的数量关系.(α大于0°且小于45°)
提 问:经过三次翻折,图形更复杂了。新增了哪条角平分线?它平分哪个角?
预 设:利用三角形内角和为180°或一个平角为180°建立等量关系。
(设计意图:从(1)中求特殊度数的角到(2)中求两个角的数量关系,体现问题设置的层层递进。)
【活动二】平行的判定的运用
如图所示,将长方形纸条沿EF、GH折叠,使得DH与BE重合.
(3)沿HF折叠后,当∠α为多少度时,可以产生新的平行线?
预 设:①当∠α=22.5°时,AG∥DB∥FC∥B2C2,AD∥HB2∥FC2∥BC;
②当∠α=30°时,B2C2∥EF∥GH;
③当∠α=45°时,B2C2∥AD;
……
(设计意图:本题具有充分的开放性。既是平行线判定定理运用能力的提升,又渗透了方程思想.三线八角是判定平行的重要基本图形,本题对培养学生从复杂图形中分离基本图形的能力有重要作用. )
环节四 总结反思,布置作业
【总结】
问题一:今天我们复行线的哪些定理?翻折带来了哪些特殊条件?
问题二:学习过程中涉及了哪些思想方法?
【作业】
必做题:作业本第一章复习题.
选做题:思考——当α大于45°,有可能出现新的平行线吗?
(设计意图:本环节要给予学生充分时间进行反思总结,梳理本节知识体系.作业布置采取分层布置,体现不同的人在数学上得到不同的发展.)
——平行线的性质与判定的复习
一、教材分析
《平行线的性质与判定的复习》,是浙教版七年级下册第一章《平行线》学习后续的复习部分。复习的主要内容是平行线的性质和判定. 本节课以翻折问题为载体,是平行线性质和判定的回顾和延伸. 本节课的学习对学生简单几何问题的推理能力和图形迁移能力的培养起着重要作用.
教学目标
知识技能:掌握平行线的判定和性质;
过程方法:经历动手折叠发现角的数量关系过程,渗透化归思想和方程思想,并逐步掌握几何说理的基本方法;
问题解决:经历添加不同条件判定平行线的过程,培养和发展逻辑思维能力和推理论证的表达能力,培养发现问题、分析问题、提出问题、解决问题的能力;
情感态度:经历性质定理、判定定理选择的过程,感受数学思考过程中的合理性、数学证明的严谨性. 认识到事物间的相互关系、相互转化,学会用辩证的观点分析事物.
三、教学重难点
项目 教学重点 教学难点
内容 平行线的性质与判定 在翻折问题中判定平行线与求角
依据 教材编排以及本课的教学目标 学生的认知特点
四、教法学法
教法:
这节课主要将“启发式”与“探究式”相结合进行教学.围绕本节课知识,引导学生经历从动手折叠直观感知,到逻辑推理证明的过程,学生积极参与,培养提出问题、分析问题、解决问题的能力.
学法:
让每一个学生积极参与课堂的知识构建,通过“自主探究”、“合作交流”等方式,由“学会”变成“会学”和“乐学”,主动经历数学知识形成的过程.
五、教学过程
环节一 激活旧知,引入课题
引 入:刚才,同学们拿到了一张长方形纸条,你能说一说它的图形特征吗?
预 设:①两组对边分别平行;
②四个角都是直角.
引 入:今天,我们就要借助这张长方形纸条,来复习平行线的相关知识.
环节二 动手操作,复习定理
【活动一】回忆平行线的性质与判定定理.
问题一:你能将一张长方形纸条折叠,使得折痕成为一组平行线吗?请动手试试并说明理由.
方法一:
方法二:
提 问:请说说你的折法,并说明折痕平行的理由.
小 结:①同旁内角互补,两直线平行;
②同位角相等,两直线平行;
③在同一平面内,垂直于同一条直线的两条直线平行;
④两直线平行,内错角相等;
⑤两直线平行,同旁内角互补;
⑥在翻折问题中,折痕即角平分线.
方法三:
提 问: 前两种折法折出了45°,90°这些特殊的角。方法三更具有一般性。是如何折出的?请你用几何语言说明折痕平行的理由.
【活动二】利用平行线的性质和判定定理进行几何说理
如图所示,将长方形纸带沿EF、GH折叠,使得DH与BE重合. 折痕GH与EF平行吗?请说明理由.
小 结:①解决翻折问题时,要先还原图形。再分清折痕平分的是哪些角。
②内错角相等,两直线平行;
③两直线平行,同位角相等。
(设计意图:在这个具有开放性的问题中,不同层次的学生可以想出不同难度的折法. 在翻折的过程中,学生从具体的动手操作中抽象出平行线的基本图形,最后进行严密的逻辑推理. )
环节三 独立思考,灵活运用
【活动一】平行的性质的运用
如图所示,将长方形纸条沿EF、GH折叠,使得DH与BE重合.
(1)若∠ =150°,求∠ 的度数.
提 问:由翻折得到哪些隐含条件?
预 设:利用平行的性质求角,会根据已知条件选择合适的方法.
(2)沿HF折叠,点B,C分别落在 , 处.∠HEF试探究α与β
的数量关系.(α大于0°且小于45°)
提 问:经过三次翻折,图形更复杂了。新增了哪条角平分线?它平分哪个角?
预 设:利用三角形内角和为180°或一个平角为180°建立等量关系。
(设计意图:从(1)中求特殊度数的角到(2)中求两个角的数量关系,体现问题设置的层层递进。)
【活动二】平行的判定的运用
如图所示,将长方形纸条沿EF、GH折叠,使得DH与BE重合.
(3)沿HF折叠后,当∠α为多少度时,可以产生新的平行线?
预 设:①当∠α=22.5°时,AG∥DB∥FC∥B2C2,AD∥HB2∥FC2∥BC;
②当∠α=30°时,B2C2∥EF∥GH;
③当∠α=45°时,B2C2∥AD;
……
(设计意图:本题具有充分的开放性。既是平行线判定定理运用能力的提升,又渗透了方程思想.三线八角是判定平行的重要基本图形,本题对培养学生从复杂图形中分离基本图形的能力有重要作用. )
环节四 总结反思,布置作业
【总结】
问题一:今天我们复行线的哪些定理?翻折带来了哪些特殊条件?
问题二:学习过程中涉及了哪些思想方法?
【作业】
必做题:作业本第一章复习题.
选做题:思考——当α大于45°,有可能出现新的平行线吗?
(设计意图:本环节要给予学生充分时间进行反思总结,梳理本节知识体系.作业布置采取分层布置,体现不同的人在数学上得到不同的发展.)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
