4.3用乘法公式分解因式(1)
图片预览




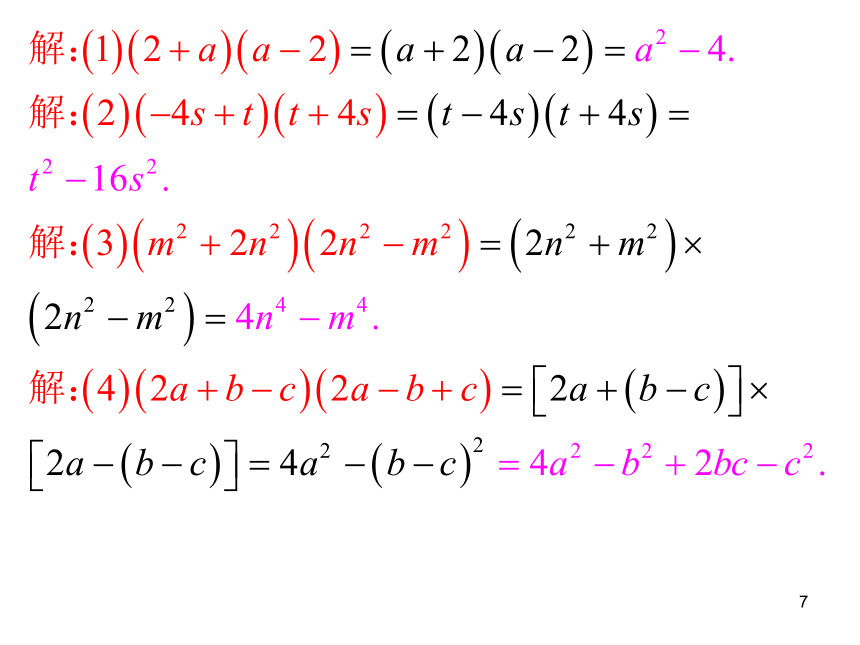




文档简介
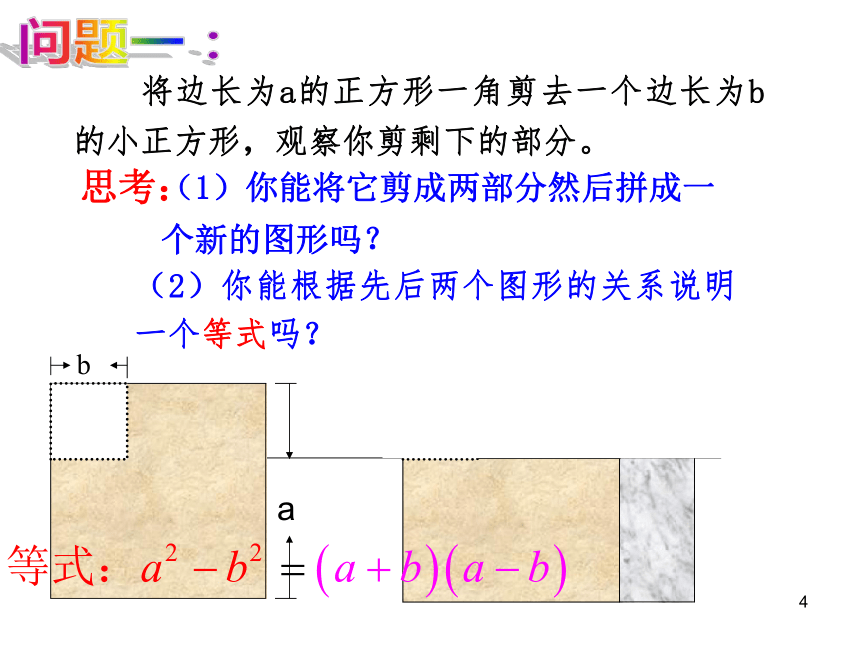
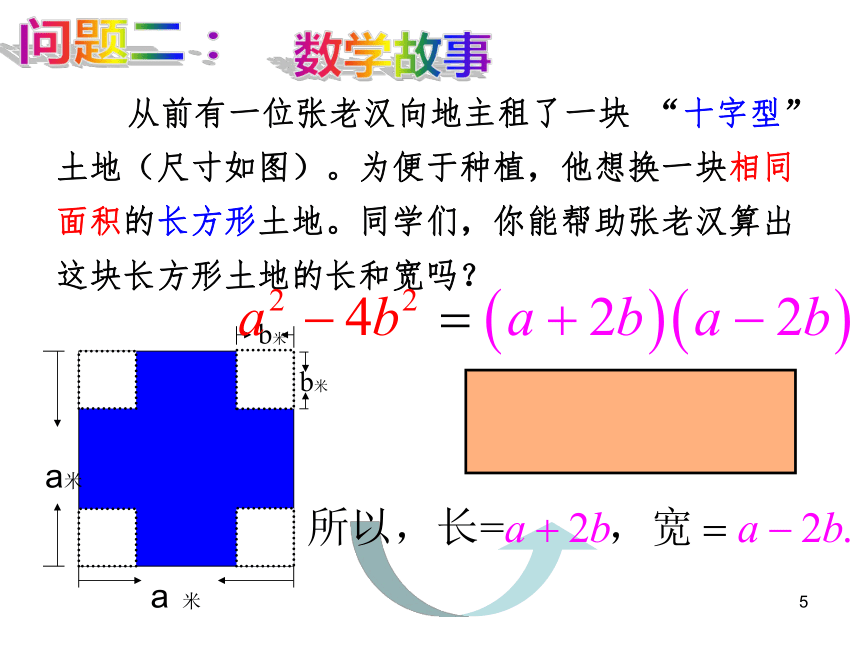
课件43张PPT。15.把下列多项式分解因式2T6解:3瑞安市东山中学4.3 用乘法公式分解因式(1)平方差公式4 将边长为a的正方形一角剪去一个边长为b的小正方形,观察你剪剩下的部分。(2)你能根据先后两个图形的关系说明一个等式吗?问题一:(1)你能将它剪成两部分然后拼成一 个新的图形吗?思考:5 从前有一位张老汉向地主租了一块 “十字型”土地(尺寸如图)。为便于种植,他想换一块相同面积的长方形土地。同学们,你能帮助张老汉算出这块长方形土地的长和宽吗? 数学故事问题二:6
.(2+a)(a-2);
2).(-4s+t)(t+4s)
.(m2+2n2)(2n2- m2) 看谁做得最快最正确!4). (2a +b-c)(2a-b+c ) 以上式子都可以用什么乘法公式简便计算?计算结果的多项式有什么共同点?问题三:计算下列各题:78学生自学探究自学课文P1031.平方差公式;2能用平方差公式分解因式的多项式的特征:(1)、由两部分组成;(2)、两部分符号相反;(3)、每部分都能写成整式(或数) 的平方的形式。9议一议观察多项式① ② ③回答下列问题:(1)这三个多项式它们有公因式吗?(2)能用提取公因式分解因式吗?
(3)这3个多项式各有什么特点?你联想到什么?没有不能①是“a”与“2”的平方差,②是“t”与“4s”的平方差, ③是“2n”
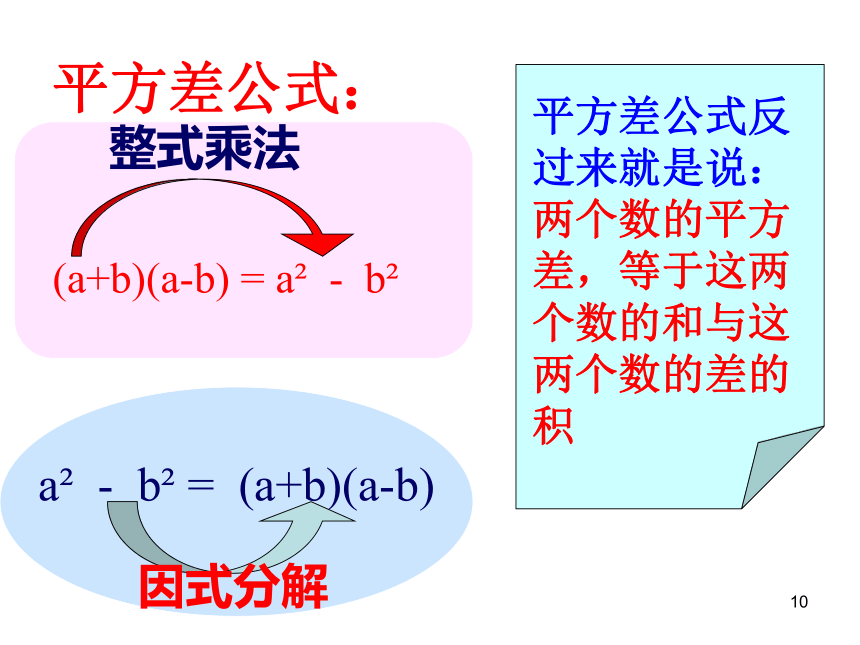
与“3m”的平方差;联想到乘法公式中的平方差公式。探一探对多项式① ② ③10平方差公式反过来就是说:两个数的平方差,等于这两个数的和与这两个数的差的积a2 - b2 = (a+b)(a-b)
因式分解整式乘法平方差公式:
(a+b)(a-b) = a2 - b211a2-b2=(a + b)(a - b)16a2-1=(4a)2-12=(4a+1)(4a-1)下列多项式能否用平方差公式分解因式?(1)4x2+y2 (2) 4x2-(-y)2
(3) -4x2-y2 (4) -4x2+y2
(5) a2-4 (6) a2+3能用平方差公式分解因式的多项式的特征:1、由两部分组成;2、两部分符号相反;3、每部分都能写成整式(或数) 的平方的形式。√√√学一学:12
(1)16a2- 1
平方差公式:a2-b2 =(a+b)(a-b)(5)x2y4-9讲解例题例1.把下列各式分解因式13 (1) x2-1 (2)m2-9
(3)x2-4y2 (4) 25x2-4
(5) 0.01s2-t2 (6) 121-4a2b2
(7) a6-81 (8)–x2+25
(9) 16a2-9b2 (10) - 4a2b2+c2 =(x+1)(x-1)=(m+3)(m-3)=(x+2y)(x-2y)=(5x+2)(5x-2)=(0.1s+t)(0.1s-t)=(11+2ab)(11-2ab)=(a3+9)(a3-9)=(5+x)(5-x)=(4a+3b)(4a-3b)=(c+2ab)(c-2ab)试一试:学生练习:14例2.把下列各式因式分解
( x + z )2- ( y + z )2
4( a + b)2 - 25(a - c)2
4a3 - 4a
(x + y + z)2 - (x – y – z )2
5) 0.5a2- 215注
意 当公式中的a、b表示多项式时,要把这两个多项式看成两个整体,分解成的两个因式要进行去括号化简,若有同类项,要进行合并。161.下列多项式可以用平方差公式分解因式吗?说说你的理由。学生练习:不可以,多项式不能看做两数的平方差。不可以,多项式不能看做两数的平方差。不可以,多项式不能看做两数的平方差。可以,多项式看做2x与y的平方差。可以,多项式看做y与2x两数的平方差。可以,多项式看做a与2两数的平方差。17平方差公式:a2-b2 =(a+b)(a-b)例3.把下列各式分解因式
① x4 - 81y4
② 2a3 - 8a 1.解:原式= (x2+ 9y2) (x2- 9y2)
= (x2+ 9y2) (x+ 3y) (x- 3y)2.解:原式=2a(a2- 4)
=2a(a+2)(a-2)181)下列各式能用平方差公式分解因式的是( )
4X2+y2 B.4 x- (-y)2 C.-4 X2-y3 D.- X2+ y2
-4a2 +1分解因式的结果应是( )
-(4a+1)(4a-1) B. -( 2a –1)(2a –1)
-(2a +1)(2a+1) D. -(2a+1) (2a-1)DD1.选一选:学生练习:193).x2-64因式分解为( ).
(x-16)(x+4); (B) (x-32)(x+32);
(C) (x+16)(x-4); (D) (x-8)(x+8).4). 64a8-b2因式分解为( ).
(A) (64a4-b)(a4+b); (B) (16a2-b)(4a2+b);
(C) (8a4-b)(8a4+b); (D) (8a2-b)(8a4+b).DC202.分解因式:(4)
(5)a4 -81
(6)- +4x2
做一做211、分解因式:
(1) 25x2-4 =(5x+2)(5x-2)(2) 4x3 -x=x(4x2-1)=x(2x+1)(2x-1)(3) a4 -81= (a2+9)(a2-9)= (a2+9)(a+3) (a-3)(4) 4x3y - 9xy3 = xy(4x2-9y2)=xy(2x+3y)(2x-3y)(5) 4( a + b )2- 25( a -c )2=(7a+2b-5c)(2b -3a+5c)=[2(a+b)]2-[5(a-c)]2=[2(a+b)+ 5(a-c)][2(a+b) - 5(a-c)](6) 4a2 - 16b2=4 (a2- 4b2)= 4 (a+ 2b) (a- 2b)学生练习:222、把下列多项式分解因式:
(1) 4x3y-9xy3
(2) 27a3bc-3ab3c
(3) x4-16学生练习:23例4、用平方差公式进行简便计算:
(1)81.52-78.52 (2)9992-9982
(3)2292-1712 (4)91×89(6)把9991分解成两个整数的积。241.把下列多项式分解因式:学生练习:25一座公园建筑的示意图如图所示,环形绿化带的外圆半径为7.5米,内圆半径为5.5米,这个环形绿化带的面积是多少?
怎样计算比较简便?解:26知识聚焦1.先提取公因式2.再应用平方差公式分解3.每个因式要化简,并且分解彻底对于分解复杂的多项式,我们应该怎么做?271、利用平方差公式法分解因式的步骤:§4.3用乘法公式分解因式(1)---平方差公式一、知识收获:平方差公式:(1).公式:
(2)文字表达式:两数的平方差等于两数的和与两数的差的积。
(3)注意:①公式中字母a、b可以表示任何数或单项式和多项式;
②若给出的多项式不具备明显平方差关系需要化成a -b 的形式。22二、能力收获:(1)优先考虑提取公因式法
(2)其次看是否能用公式法 (如平方差公式)
(3)务必检查是否分解彻底了2.能用平方差公式分解因式的多项式的特征:(1)、由两部分组成;(2)、两部分符号相反;(3)、每部分都能写成整式(或数) 的平方的形式。28【1】、复习、整理、巩固今天所学知识。一、必做题:1、作业本(2)第31--32页T1—T7;
2、参书第104页A组题T1—T3;
3.课时特训第64、65页T1—T16
二、选做题:1、参书第105页B、C组题T4--T7;
2.拓展探究题:参看幻灯片第28--40号。
三、抄写第26张幻灯片的内容。【2】、书面作业布置作业:292、计算:25 × 2652-1352 × 25拓展提高:1、分解因式:3、求(2+1)(22+1)(24+1)……(232+1)+1的个位数字;4、若248-1能被60与70之间的两个整数整除,这两个整数分别是 与 ;5、已知,x+ y =7,x-y =5,求代数式 x 2- y2-2y+2x的值.6、若n是整数,证明(2n+1) -(2n-1) 是8的倍数.2230今年,我的年龄和我表妹年龄的平方差是87。那你和你表妹今年分别几岁了?聪明的同学,你们能算出来吗?数学乐园等一下,
我能算出来!31321、分解因式:2、计算:3334354、若2 -1能被60与70之间的两个整
数整除,这两个整数分别是 与 ;486365365、已知,x+ y =7,x-y =5,求代数式
x - y -2y+2x的值.22376、若n是整数,证明(2n+1) -(2n-1)
是8的倍数.2238拓展提高: 1、英国数学家狄摩根在青年时代,曾有人问他:“今年多大年龄?”狄摩根想了想说:“今年,我的年龄和我弟弟年龄的平方差是141,你能算出我的年龄和我弟弟的年龄吗?”假设狄摩根的年龄为x岁,他弟弟的年龄为 y岁,你能算出他们的年龄吗?3940 2、把一块纸板形状如图,请剪一个面积和这块纸板相等的长方形纸板,求出这个长方形纸板的长和宽,并画出图形。bab a2-b2=(a+b)(a-b)拓展提高:413、观察下表,你还能继续往下写吗?你发现了什么规律?能用因式分解来说明你发现的规律吗?42做一做 如图,在一块边长为 acm 的正方形的四角,各剪去一个边长为bcm的正方形,求剩余部分的面积。如果a=3.6,b=0.8呢?43再见你发现了什么规律?
用因式分解来说明规律吗?
.(2+a)(a-2);
2).(-4s+t)(t+4s)
.(m2+2n2)(2n2- m2) 看谁做得最快最正确!4). (2a +b-c)(2a-b+c ) 以上式子都可以用什么乘法公式简便计算?计算结果的多项式有什么共同点?问题三:计算下列各题:78学生自学探究自学课文P1031.平方差公式;2能用平方差公式分解因式的多项式的特征:(1)、由两部分组成;(2)、两部分符号相反;(3)、每部分都能写成整式(或数) 的平方的形式。9议一议观察多项式① ② ③回答下列问题:(1)这三个多项式它们有公因式吗?(2)能用提取公因式分解因式吗?
(3)这3个多项式各有什么特点?你联想到什么?没有不能①是“a”与“2”的平方差,②是“t”与“4s”的平方差, ③是“2n”
与“3m”的平方差;联想到乘法公式中的平方差公式。探一探对多项式① ② ③10平方差公式反过来就是说:两个数的平方差,等于这两个数的和与这两个数的差的积a2 - b2 = (a+b)(a-b)
因式分解整式乘法平方差公式:
(a+b)(a-b) = a2 - b211a2-b2=(a + b)(a - b)16a2-1=(4a)2-12=(4a+1)(4a-1)下列多项式能否用平方差公式分解因式?(1)4x2+y2 (2) 4x2-(-y)2
(3) -4x2-y2 (4) -4x2+y2
(5) a2-4 (6) a2+3能用平方差公式分解因式的多项式的特征:1、由两部分组成;2、两部分符号相反;3、每部分都能写成整式(或数) 的平方的形式。√√√学一学:12
(1)16a2- 1
平方差公式:a2-b2 =(a+b)(a-b)(5)x2y4-9讲解例题例1.把下列各式分解因式13 (1) x2-1 (2)m2-9
(3)x2-4y2 (4) 25x2-4
(5) 0.01s2-t2 (6) 121-4a2b2
(7) a6-81 (8)–x2+25
(9) 16a2-9b2 (10) - 4a2b2+c2 =(x+1)(x-1)=(m+3)(m-3)=(x+2y)(x-2y)=(5x+2)(5x-2)=(0.1s+t)(0.1s-t)=(11+2ab)(11-2ab)=(a3+9)(a3-9)=(5+x)(5-x)=(4a+3b)(4a-3b)=(c+2ab)(c-2ab)试一试:学生练习:14例2.把下列各式因式分解
( x + z )2- ( y + z )2
4( a + b)2 - 25(a - c)2
4a3 - 4a
(x + y + z)2 - (x – y – z )2
5) 0.5a2- 215注
意 当公式中的a、b表示多项式时,要把这两个多项式看成两个整体,分解成的两个因式要进行去括号化简,若有同类项,要进行合并。161.下列多项式可以用平方差公式分解因式吗?说说你的理由。学生练习:不可以,多项式不能看做两数的平方差。不可以,多项式不能看做两数的平方差。不可以,多项式不能看做两数的平方差。可以,多项式看做2x与y的平方差。可以,多项式看做y与2x两数的平方差。可以,多项式看做a与2两数的平方差。17平方差公式:a2-b2 =(a+b)(a-b)例3.把下列各式分解因式
① x4 - 81y4
② 2a3 - 8a 1.解:原式= (x2+ 9y2) (x2- 9y2)
= (x2+ 9y2) (x+ 3y) (x- 3y)2.解:原式=2a(a2- 4)
=2a(a+2)(a-2)181)下列各式能用平方差公式分解因式的是( )
4X2+y2 B.4 x- (-y)2 C.-4 X2-y3 D.- X2+ y2
-4a2 +1分解因式的结果应是( )
-(4a+1)(4a-1) B. -( 2a –1)(2a –1)
-(2a +1)(2a+1) D. -(2a+1) (2a-1)DD1.选一选:学生练习:193).x2-64因式分解为( ).
(x-16)(x+4); (B) (x-32)(x+32);
(C) (x+16)(x-4); (D) (x-8)(x+8).4). 64a8-b2因式分解为( ).
(A) (64a4-b)(a4+b); (B) (16a2-b)(4a2+b);
(C) (8a4-b)(8a4+b); (D) (8a2-b)(8a4+b).DC202.分解因式:(4)
(5)a4 -81
(6)- +4x2
做一做211、分解因式:
(1) 25x2-4 =(5x+2)(5x-2)(2) 4x3 -x=x(4x2-1)=x(2x+1)(2x-1)(3) a4 -81= (a2+9)(a2-9)= (a2+9)(a+3) (a-3)(4) 4x3y - 9xy3 = xy(4x2-9y2)=xy(2x+3y)(2x-3y)(5) 4( a + b )2- 25( a -c )2=(7a+2b-5c)(2b -3a+5c)=[2(a+b)]2-[5(a-c)]2=[2(a+b)+ 5(a-c)][2(a+b) - 5(a-c)](6) 4a2 - 16b2=4 (a2- 4b2)= 4 (a+ 2b) (a- 2b)学生练习:222、把下列多项式分解因式:
(1) 4x3y-9xy3
(2) 27a3bc-3ab3c
(3) x4-16学生练习:23例4、用平方差公式进行简便计算:
(1)81.52-78.52 (2)9992-9982
(3)2292-1712 (4)91×89(6)把9991分解成两个整数的积。241.把下列多项式分解因式:学生练习:25一座公园建筑的示意图如图所示,环形绿化带的外圆半径为7.5米,内圆半径为5.5米,这个环形绿化带的面积是多少?
怎样计算比较简便?解:26知识聚焦1.先提取公因式2.再应用平方差公式分解3.每个因式要化简,并且分解彻底对于分解复杂的多项式,我们应该怎么做?271、利用平方差公式法分解因式的步骤:§4.3用乘法公式分解因式(1)---平方差公式一、知识收获:平方差公式:(1).公式:
(2)文字表达式:两数的平方差等于两数的和与两数的差的积。
(3)注意:①公式中字母a、b可以表示任何数或单项式和多项式;
②若给出的多项式不具备明显平方差关系需要化成a -b 的形式。22二、能力收获:(1)优先考虑提取公因式法
(2)其次看是否能用公式法 (如平方差公式)
(3)务必检查是否分解彻底了2.能用平方差公式分解因式的多项式的特征:(1)、由两部分组成;(2)、两部分符号相反;(3)、每部分都能写成整式(或数) 的平方的形式。28【1】、复习、整理、巩固今天所学知识。一、必做题:1、作业本(2)第31--32页T1—T7;
2、参书第104页A组题T1—T3;
3.课时特训第64、65页T1—T16
二、选做题:1、参书第105页B、C组题T4--T7;
2.拓展探究题:参看幻灯片第28--40号。
三、抄写第26张幻灯片的内容。【2】、书面作业布置作业:292、计算:25 × 2652-1352 × 25拓展提高:1、分解因式:3、求(2+1)(22+1)(24+1)……(232+1)+1的个位数字;4、若248-1能被60与70之间的两个整数整除,这两个整数分别是 与 ;5、已知,x+ y =7,x-y =5,求代数式 x 2- y2-2y+2x的值.6、若n是整数,证明(2n+1) -(2n-1) 是8的倍数.2230今年,我的年龄和我表妹年龄的平方差是87。那你和你表妹今年分别几岁了?聪明的同学,你们能算出来吗?数学乐园等一下,
我能算出来!31321、分解因式:2、计算:3334354、若2 -1能被60与70之间的两个整
数整除,这两个整数分别是 与 ;486365365、已知,x+ y =7,x-y =5,求代数式
x - y -2y+2x的值.22376、若n是整数,证明(2n+1) -(2n-1)
是8的倍数.2238拓展提高: 1、英国数学家狄摩根在青年时代,曾有人问他:“今年多大年龄?”狄摩根想了想说:“今年,我的年龄和我弟弟年龄的平方差是141,你能算出我的年龄和我弟弟的年龄吗?”假设狄摩根的年龄为x岁,他弟弟的年龄为 y岁,你能算出他们的年龄吗?3940 2、把一块纸板形状如图,请剪一个面积和这块纸板相等的长方形纸板,求出这个长方形纸板的长和宽,并画出图形。bab a2-b2=(a+b)(a-b)拓展提高:413、观察下表,你还能继续往下写吗?你发现了什么规律?能用因式分解来说明你发现的规律吗?42做一做 如图,在一块边长为 acm 的正方形的四角,各剪去一个边长为bcm的正方形,求剩余部分的面积。如果a=3.6,b=0.8呢?43再见你发现了什么规律?
用因式分解来说明规律吗?
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
