平行线的判定(一)

课件23张PPT。义务教育课程标准实验教科书　
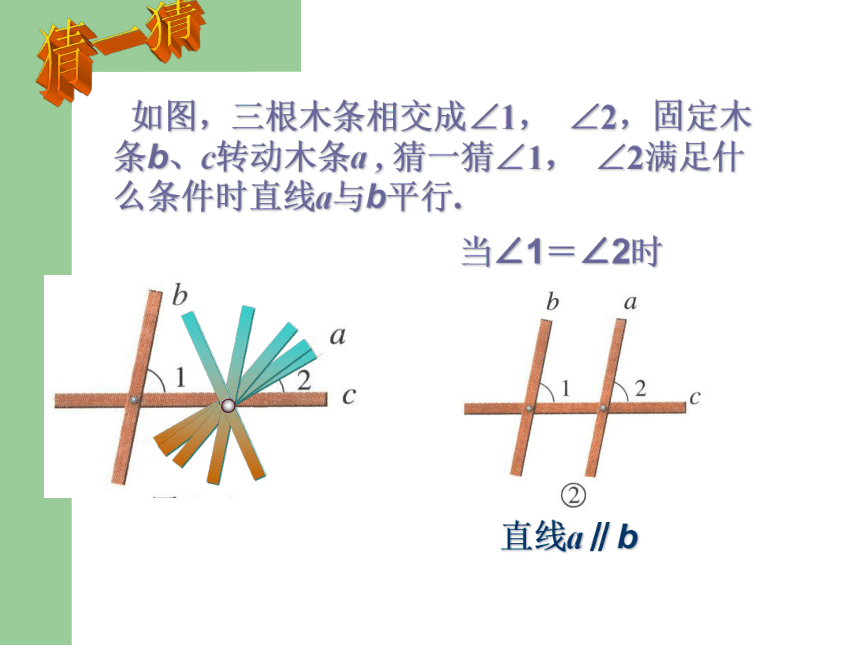
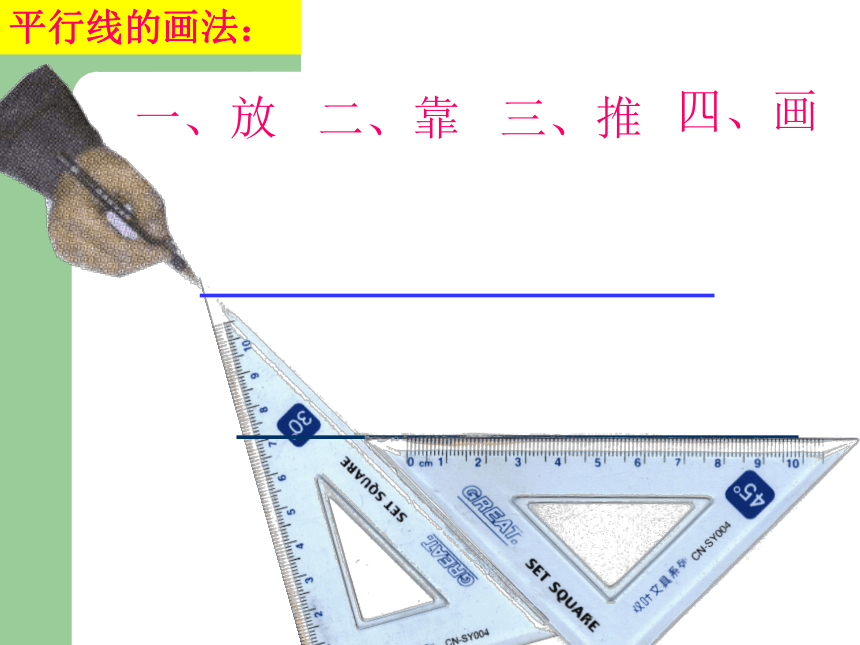
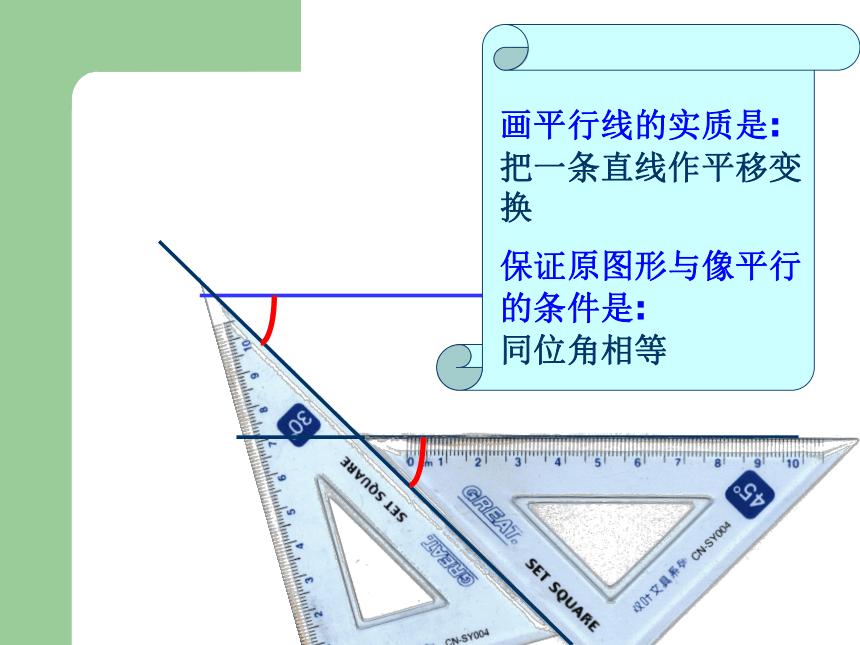
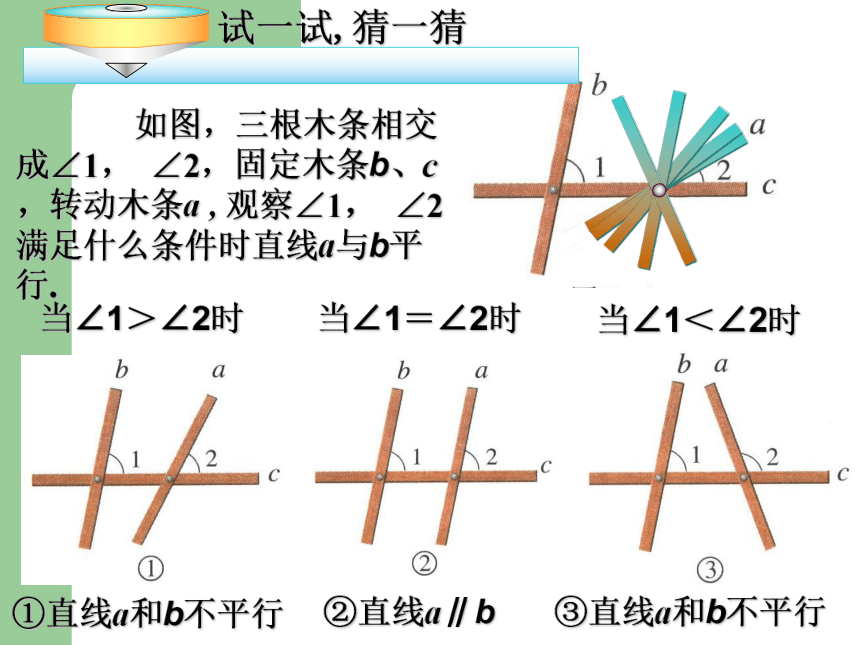
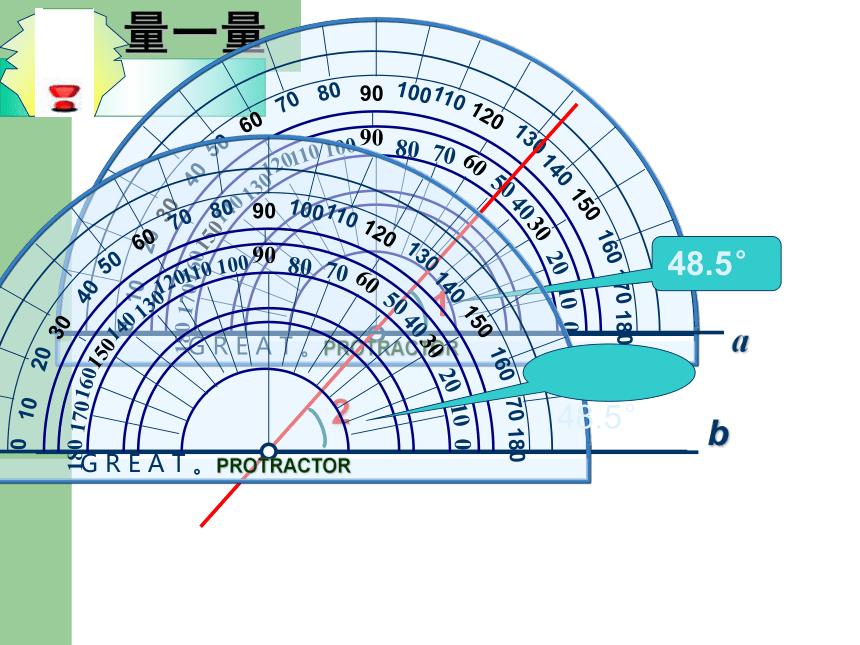
浙江版《数学》八年级上册 1.3 平行线的判定(一) 如图，三根木条相交成∠1， ∠2，固定木条b、c转动木条a , 猜一猜∠1， ∠2满足什么条件时直线a与b平行.当∠1＝∠2时直线a∥b猜一猜一、放二、靠三、推四、画平行线的画法： 如图，三根木条相交成∠1， ∠2，固定木条b、c，转动木条a , 观察∠1， ∠2满足什么条件时直线a与b平行.当∠1＝∠2时①直线a和b不平行②直线a∥b③直线a和b不平行48.5°21 48.5°即：同位角相等，两直线平行平行线的判定方法：２∵∠１＝ ∠２ ∴a∥b（同位角相等，两直线平行）推理格式(几何叙述)：两条直线被第三条直线所截，如果同位角相等，
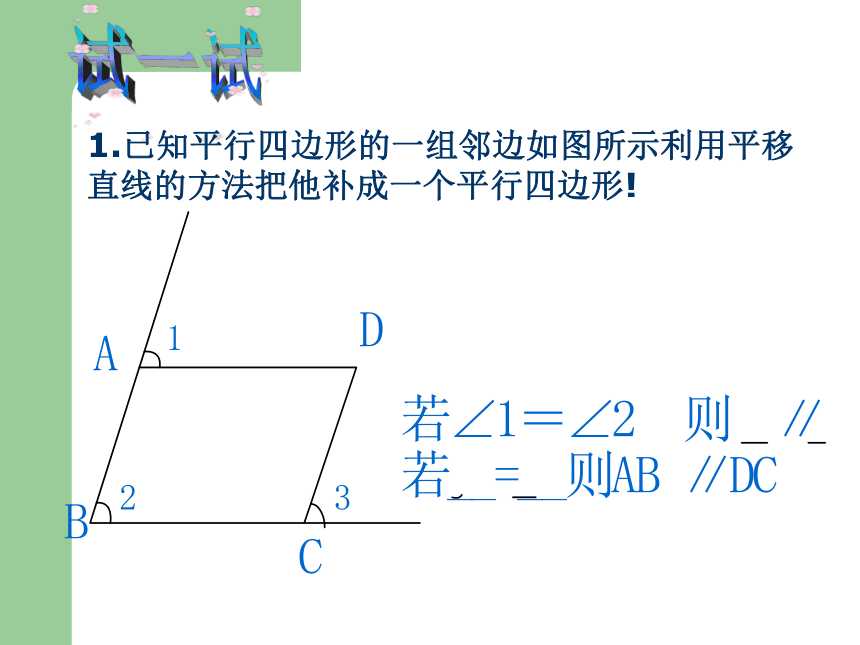
那么这两条直线平行．试一试1.已知平行四边形的一组邻边如图所示利用平移直线的方法把他补成一个平行四边形!课堂练习：火眼金睛，找出图中的平行线如果∠ADE=∠ABC,则＿＿∥ ＿＿如果∠ACD=∠F, 则＿＿∥ ＿＿如果∠DEC=∠BCF,则＿＿∥ ＿＿DE BCCD BFDE BC例 1已知直线l1 ，l2被l3所截,如图，
∠1＝45°,∠2＝135°,试
判断l1与l2是否平行.并说明理由.解： l1 ∥ l2理由如下：∵ ∠2＋∠3＝180°，∠2＝135° ∴∠3＝180°－∠2＝180°－135°＝45°∵∠1＝45° ∴∠1＝∠3 ∴ l1 ∥ l2（同位角相等，两直线平行）要判断两直线是否
平行,首先应该看
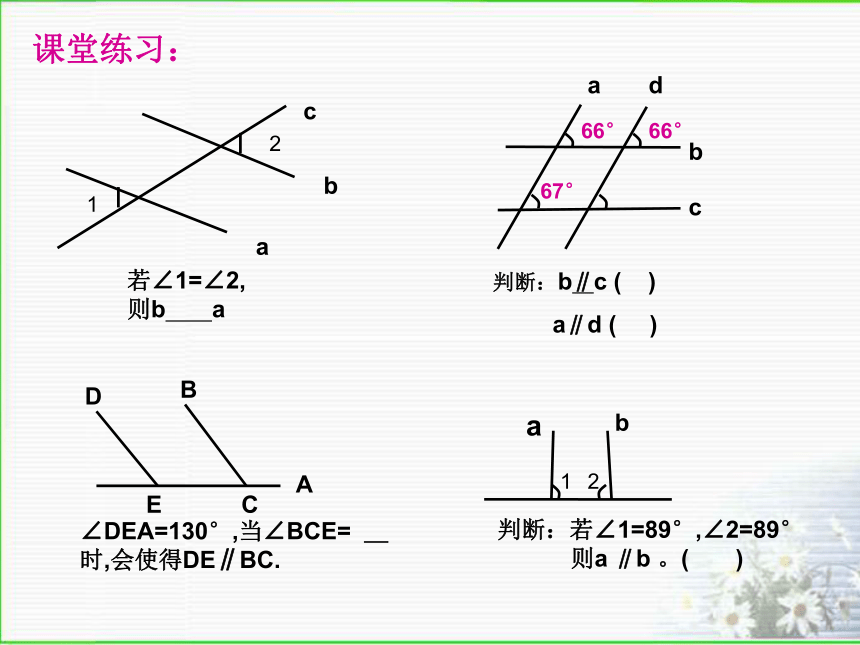
同位角是否相等.想一想 “在同一平面内,垂直于同一直线的两条直线互相平行”是否可以看成平行线判定方法的特殊情形?若a⊥b,c⊥b, 那么∠1=∠2=90°则a　　c学以自用：街道两侧路灯的柱子是否互相平行？为什么？⊥练一练1、如图：已知直线l1，l2被直线AB所截，AC⊥l2于点C。若∠1=50°，∠2=40°，则l1与l2平行吗？请说明理由。以下是小明同学的解题过程。你认同吗？有何不妥？解：
　 ∵ AC⊥l2于点C ，
∴∠ACB＝90°，
又 ∵∠2＝40°，
∴∠ABC＝50°，
　∵∠１＝ 50°
　∴∠１＝∠ＡＢＣ
∴l1∥l2（同位角相等，两直线平行）
如图，已知直线l1，l2被直线l３所截，判断l1，l2是否平行１２ 某人骑自行车从Ａ地出发，沿正东方向前进至Ｂ处后，右转１５°，沿直线向前行驶到Ｃ处。（如图）这时他想仍按正东方向行驶，那么他应怎样调整行驶方向？请画出他应继续行驶的路线，并说明理由。Ｃ想一想试一试如图，哪些直线平行，哪些直线不平行?请说明理由.理一理 你学到了什么？
你认为还有什么不懂的？
你有什么经验与收获让同学们共享呢？例2如图,已知∠ABD=∠ACE，BF、CG分别是∠ABD、∠ACE的平分线，请判断BF与CG是否平行，并说明理由。解： BF∥CG∴ ∠1＝∠2同位角相等，两直线平行 （1）如图1，∠C＝57°，
当∠ABE＝ °时，就能使BE∥CD. （2）如图2 ， ∠1＝120°,∠2＝60°．
问a与b的关系？ 图1图2a∥b ABECD12ab 573c想一想1.如图，AB⊥BC于B，
∠1=125°，∠2=35°，
请说明l1∥l2的理由。2.如图，∠B=∠D+∠C，
试判断AB与DE是否平行，
并说明理由。小结通过今天的学习,
能说说你的收获和体会吗?
你有什么经验与收获让同学们共享呢？ 1、判定两直线平行的方法：
同位角相等，两直线平行。2、用“同位角相等，两直线平行”判定两直线平行。能进行简单的推理和表述。动一动你能用一张不规则的纸折出两条平行的直线吗？说说你的折法。Bye-Bye