4.3用乘法公式分解因式（1）

课件23张PPT。§4.3用乘法公式分解因式（1）
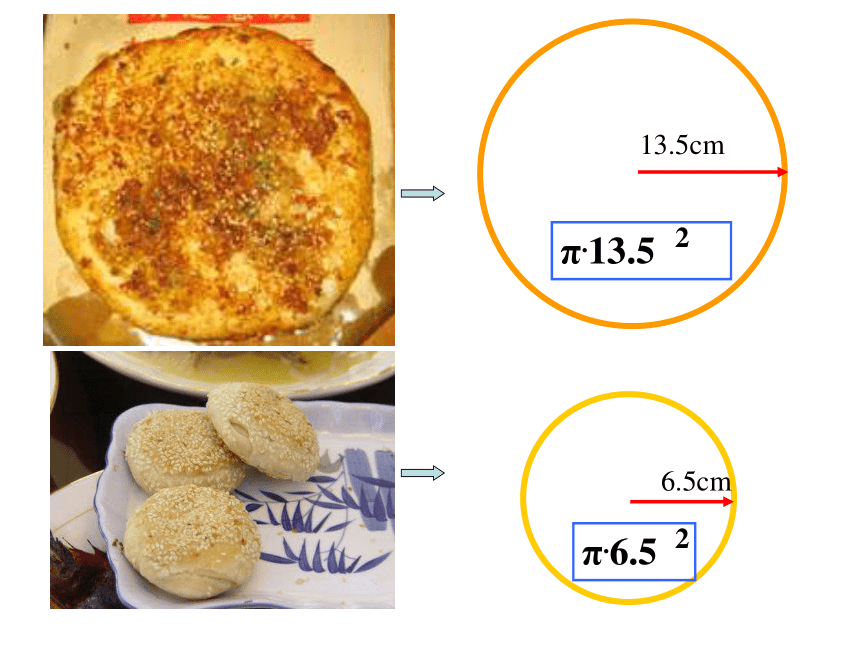
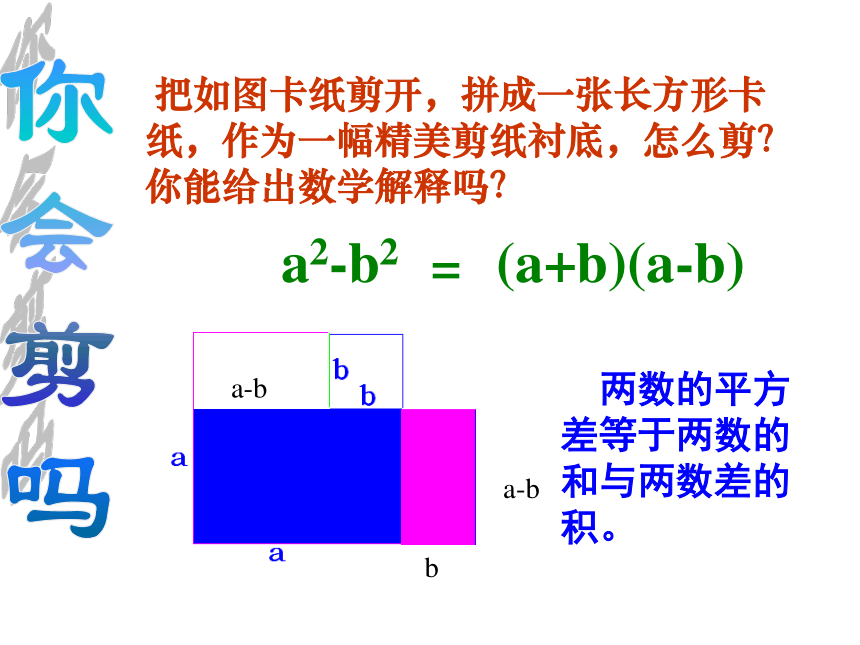
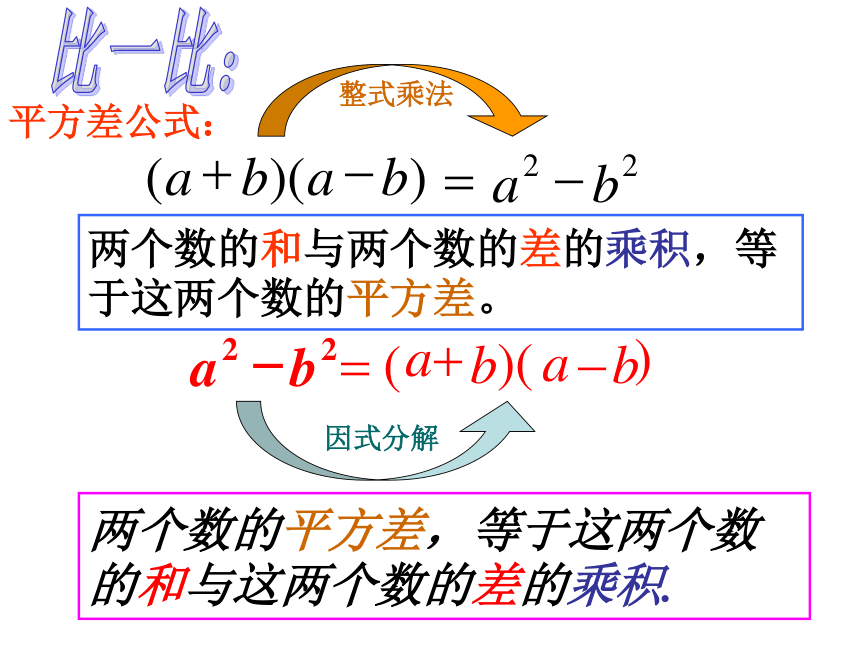
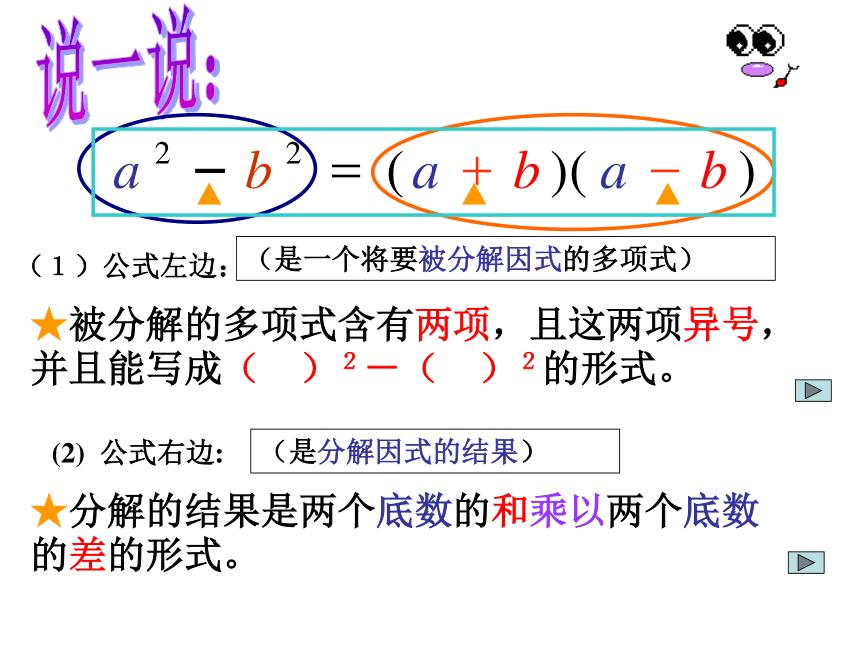
运用平方差公式因式分解(若π取3）=420！两者面积之差为（列出算式）：=3×（13.52 － 6.52 ）=3 ×20 ×7?把如图卡纸剪开，拼成一张长方形卡纸，作为一幅精美剪纸衬底，怎么剪？你能给出数学解释吗？ a-b a-b b a-b a2-b2(a+b)(a-b)=你会剪吗 两数的平方差等于两数的和与两数差的积。 比一比：两个数的和与两个数的差的乘积，等于这两个数的平方差。两个数的平方差，等于这两个数的和与这两个数的差的乘积.平方差公式：说一说：（１）公式左边：（是一个将要被分解因式的多项式）★被分解的多项式含有两项，且这两项异号，并且能写成（　）２－（　）２的形式。(2) 公式右边:（是分解因式的结果）★分解的结果是两个底数的和乘以两个底数的差的形式。a2-b2=(a + b)(a - b)
=(4a)2-12=(4a+1)(4a-1)下列多项式能否用平方差公式分解因式？说说你的理由。（1）4x2+y2 (2) 4x2-(-y)2
(3) -4x2-y2 (4) -4x2+y2
(5) a2-4 (6) a2+3能用平方差公式分解因式的多项式的特征：
1、由两部分组成；2、两部分符号相反；3、每部分都能写成某个式子的平方。
能能能不能不能不能运用a2-b2=(a+ b)(a- b)
例1:把下列各式分解因式：解:（1）原式=（2p)2-(mn)2= (2p+mn)(2p-mn)说明:公式中的a、b可以是单项式(数字、字母)、还可以是多项式.分解因式最后结果中如果有同类项，一定要合并同类项。小试牛刀（3）原式 =[(x+z)+(y+z)][(x+z)- (y+z)] =(x+y+2z)(x-y) =(x+z+y+z)(x+z- y-z) 1.判断下列利用平方差公式分解因式是否正确,不对,请改正(3) -9+4x2=(2x-3)(2x+3)(2) -a4+b2=(a2+b)(a2-b) (5) a2-(b+c)2=(a+b+c)(a-b+c)(6) s2-t2=(-s+t)(-s-t)××(b+a2)(b-a2)(a+b+c)(a-b-c)√√(s-t)(s+t)a2-b2=(a+b)(a-b)==[-(s-t)][-(s+t)](4) -1-x2=(1-x)(1+x)(1) x2-4y2=(x+4y)(x-4y)××(x+2y)(x-2y) 不能分解因式判断抢答题：=(4x+y) (4x －y)=(2k+5mn) (2k －5mn)2.把下列各式分解因式：a2 － b2= (a ＋ b) (a － b) 看谁快又对= (a+8) (a －8)当场编题，考考你！参照对象：结论：
公式中的a、b无论表示数、单项式、还是多项式，只要被分解的多项式能转化成平方差的形式，就能用平方差公式因式分解。ma+mb=m(a+b) m是各项的公因式
a2-b2=(a+b)(a-b)知识加油站合作学习例2. 分解因式4x3y-9xy3(2)提取公因式后,多项式还能继续分解因式吗?4x3y-9xy3=xy(4x2-9y2)4x3y-9xy3=xy (4x2-9y2)=xy(2x+3y)(2x-3y)(1)能分解因式吗?用什么方法?[注意]: 1.一般地,因式分解时有公因式先提公因式
2.因式分解时要分解彻底。正确率+速度=效率(2) 0.01s2-t2(1) 16-a2(4) -1+9x2(5) (a-b)2-(c-b)2(6) -(x+y)2+(x-2y)2解:原式=(4+a)(4-a)解:原式=(0.1s+t)(0.1s-t)解:原式=(3x-1)(3x+1)解:原式=(a-c)(a+c+2b)解:原式=-3y(2x-y)a2-b2=(a+b)(a-b)做一做平方差公式:a2-b2 =(a+b)(a-b) 把下列各式分解因式
① x4 - 81y4 ② 2a3 - 8a
1.解:原式= (x2+ 9y2) (x2- 9y2)
= (x2+ 9y2) (x+ 3y) (x- 3y)2.解:原式=2a(a2- 4)
=2a(a+2)(a-2)挑战极限合作探究 (1)能提取公因式。
993-99 =99(992-1) （2）还能继续分解
993-99=99(99+1)(99-1)
=99x100x98解： 4x3y-9xy3
=xy(4x2-9y2)
=xy[(2x)2-(3y)2]
=xy(2x+3y)(2x-3y)
结论：
993-99能被100整除。 记得要提取公因式！数学医院诊断分析：
公式理解不准确，不能很好的把握公式中的项， 4x2–y2中4x2 相当于a2 ,则2x相当于“a”.诊断分析：
综合运用提取公因式，公式法公解因式时，提公因式后，另一个因式还可以继续分解，同学们千万要注意分解完毕后对结果进行检查，看是否分解彻底了。正确分解：4x2–y2=(2x+y)(2x-y )= (x2+y2) (x+y)(x-y )问题在哪里？=4 (3a+2b)(a+3b)补充分解：（1）形如___________形式的多项式可以用平方差公式分解因式。（3）因式分解要_________（2）因式分解通常先考虑______________方法。课堂.小结提取公因式法彻底大显身手1.分解因式：
（1）4x3-x
( 2 ) a4-81
（3）(3x－4y）2－（4x+3y）2
（4）16（3m－2n）2－25（m－n）2
?
2、计算
（1）9992－9982
（2）25 × 2652－1352 × 25拓展提高3、若n为整数，则（2n＋1)2－(2n－1)2能被
8整除吗?请说明理由.4. 运用本节所学的知识，把9991分解成两个
整数的积.5、计算 (1－ 1/22 ) ·(1 －1/32 ) ·(1 －1/42) …
(1 －1/20052 ) ·(1 －1/20062 )的值,
从中你可以发现什么规律? 在日常生活中如上网等都需要密码.
有一种因式分解法产生的密码方便记忆又不易破译.
例如用多项式x4-y4因式分解的结果来设置密码, 当取x=9,y=9时,可得一个六位数的密码“018162”.你想知道这是怎么来的吗?小明选用多项式4x3-xy2，取x=10,y=10时。用上述方法产生的密码是什么?(写出一个即可)知识探究大显身手 杭州湾跨海大桥打下的一根用特殊材料制成的桩管
(横截面如图所示),它的外半径为R米,内半径为r米.已知外半径与内半径和为2米,外半径与内半径差为0.3米,
求横截面面积(结果保留 )Rr英国数学家狄摩根在青年时代,曾有人他:“今年多大年龄？”狄摩根想了想说：“今年，我的年龄和我弟弟年龄的平方差是141，你能算出我的年龄和我弟弟的年龄吗？”假设狄摩根的年龄为x岁，他弟弟的年龄为 y岁，你能算出他们的年龄吗？拓展训练:再 见