4.1 因式分解
图片预览









文档简介
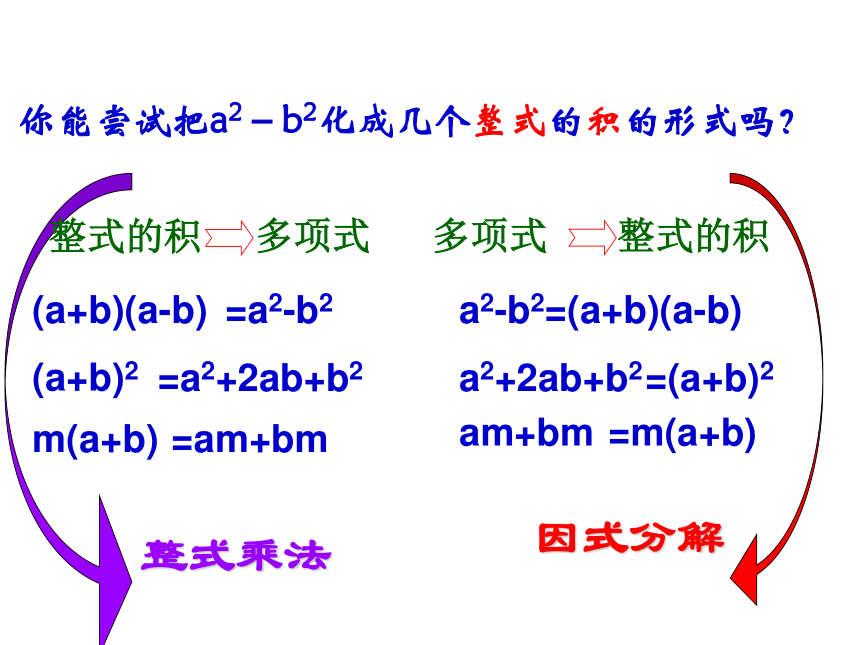
课件32张PPT。4.1 因式分解(3)a=2005,b=2003。比一比,看谁快!当a,b取下列值时,计算a2-b2的值。(1)a=5,b=3;(2)a=10,b=8;a2-b2=25-9=16a2-b2=100-64=36a2-b2=?轻松一刻计算:2×3×5=30 这是整数乘法运算,30 =2×3×5是什么运算呢?(因数分解)2×3×530整数乘法因数分解a2-b2=(a+b)(a-b)=(a+b)2=m(a+b)(a+b)(a-b)(a+b)2m(a+b)=a2-b2=a2+2ab+b2 =am+bm整式的积多项式多项式整式的积a2+2ab+b2am+bm 你能尝试把a2-b2化成几个整式的积的形式吗?(1)a(a-1)=(3)(a+1)2 =(2)(a+b)(a-b)=计算:a2-a = a(a-1)a2+2a+1 =(a+1)2a2 –b2 =(a+b)(a-b)a2-aa2-b2a2+2a+1整式乘法 因式分解一般地,把一个多项式化成几个整式的积的形式,叫做因式分解.反之反之反之观察以上左边三个等式和右边三个等式,
它们有什么不同的特点 .左边是右边是因此我们把左边这种变形叫做整式的乘法
右边这种变形叫做多项式的因式分解因式分解计算下列各式:做一做 比一比:整式乘法因式分解与整式乘法的关系 说明:
从左到右是因式分解,其特点是:由和差形式(多项式)转化成整式的积的形式;
从右到左是整式乘法,其特点是:由整式积的形式转化成和差形式(多项式). 结论:因式分解与整式乘法是互逆的关系. 因式分解
a2-b2 (a+b)(a-b)
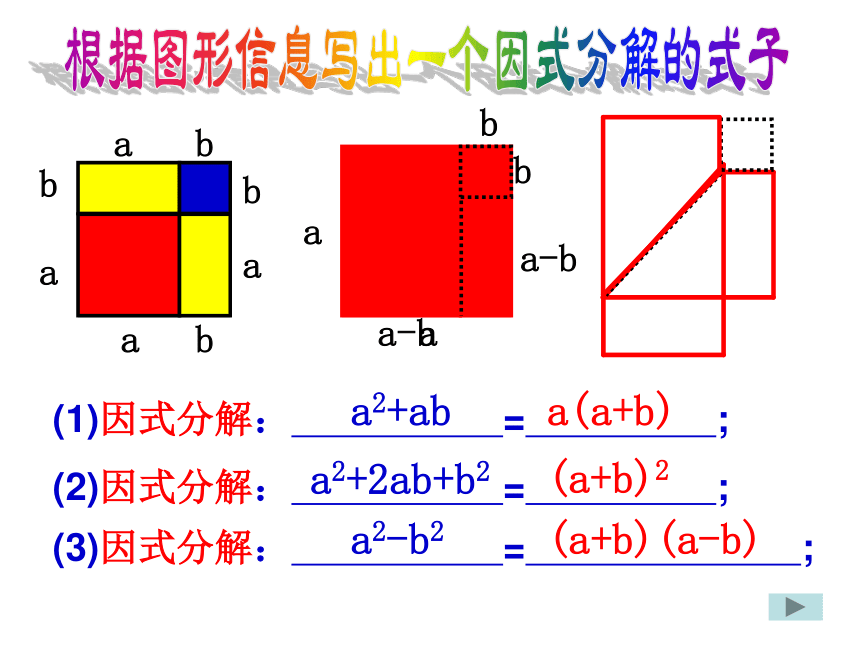
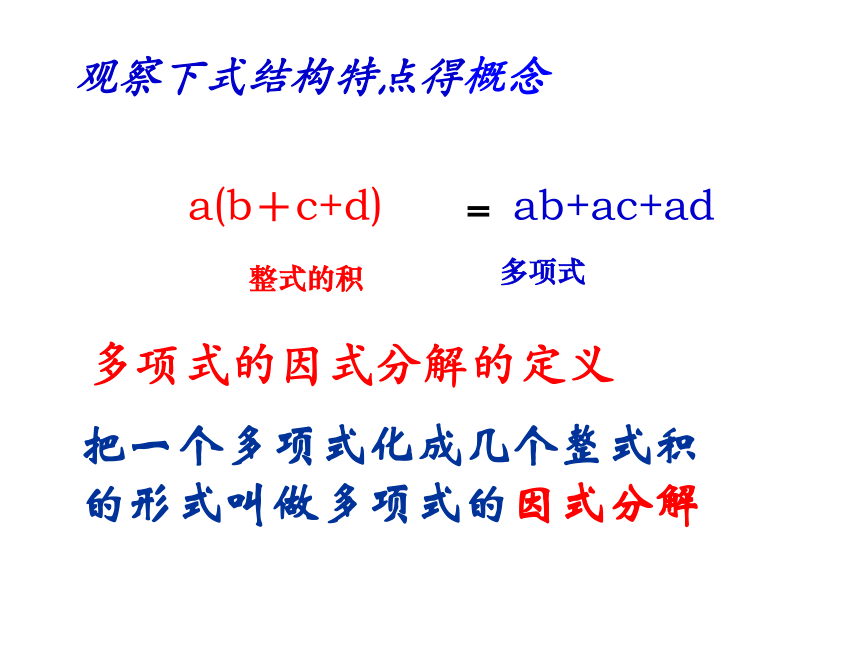
整式乘法根据图形信息写出一个因式分解的式子aaba(1)因式分解: = ;a2+abbb(2)因式分解: = ;a2+2ab+b2(a+b)2a(a+b)abaabba-ba-b(3)因式分解: = ;a2-b2(a+b)(a-b)a(b+c+d)=ab+ac+ad观察下式结构特点得概念多项式的因式分解的定义把一个多项式化成几个整式积的形式叫做多项式的因式分解整式的积多项式练习一 理解概念判断下列各式哪些是整式乘法?哪些是因式分解?
(1).x2-4y2=(x+2y)(x-2y)
(2).2x(x-3y)=2x2-6xy
(3).(5a-1)2=25a2-10a+1
(4).x2+4x+4=(x+2)2
(5).(a-3)(a+3)=a2-9
(6).m2-4=(m+4)(m-4)
(7).2 πR+ 2 πr= 2 π(R+r)因式分解整式乘法整式乘法因式分解整式乘法不是因式分解因式分解辨一辨(1)(2)(3)(4)(5)(6)(7)是不是不是不是不是不是不是下列代数式从左到右的变形是因式分解吗?因式分解: 把一个多项式转化成几个整式
的积的形式.X-4= (x≥0)是因式分解吗?(1)因式分解是对
多项式而言的一种变形;
(2)因式分解的结果
仍是几个整式的积的形式; 再来辨一辨 以上都不是因式分解填空:(1)∵m(a+b)=ma+mb
∴ma+mb= ( )( );
(2)∵(a+4)(a-3) = a2+a-12
∴a2+a-12 = ( )( );m a+ba+4 a-3 你能利用因式分解与整式乘法之间的关系,举出几个因式分解的例子吗?连一连: 试一试 你能用几种不同的方法计算 10032-10022,哪种方法最简单? 10032-10022 =(1003+1002)(1003-1002) =2005×1 =2005看谁算得快(1)若a=1001,b=999,则a2-b2=___________;
(2)若a=99,b=-1,则a2-2ab+b2=_______;
(3)若x=-3,则20x2+60x=____________。
(1)a2-b2=(a+b)(a-b)=(1001+999)(1001-999)=4000(2)a2-2ab+b2=(a-b) 2=(99+1)2 =10000(3)20x2+60x= 20x(x+3)= 20× (-3)(-3+3)=0。4000100000 小结 因式分解学习目标1.理解因式分解的概念2.会判定一个从左到右的恒等变形是不是因式分解3.学会运用因式分解的方法来解题重点:理解因式分解的概念难点:理解因式分解与整式乘法的相互关系,
并运用它们之间的相互关系寻找因式分解的方法关键点:会判定一个从左到右的恒等变形是不是因式
分 解的关键:左边必须是多项式,右边是几
个整式的积
慈溪江滨公园修建了三块长方形的绿化草坪,它们的宽都是8㎝,长分别是55.5㎝,24.4㎝,20.1㎝,那么这些绿化带的面积之和是多少? 855.5+24.4+20.1=100你能解决吗?8×55.5+8×24.4+8×20.1
=8×(55.5+24.4+20.1)(1)若(a+5)(a+2)=a2+7a+10, (2)若 x2+mx-n能分解成(x-2)(x-5), 新知知多少则a2+7a+10=( )( )则m=____,n=____.(3)若x2-6x+m=(x-4)(x-2 ),
则m=____。8 993-99能被100整除吗?你是怎样想的? 与同伴交流. 小明是这样想的:
993-99=99×992-99 ×1
=99 ×(992-1)
=99 (99+1)(99-1)
= 99×100×98
所以, 993-99能被100整除.
你知道每一步的根据吗?
想一想: 993-99还能被哪些整数整除?想一想?智力抢答(1)1012-992=(2)872+87×13=(3)512-2×51+1=(4)20102-2010×2009=真厉害!400870025002010再想一想?如果2x2+mx-2可分解因式为
(2x+1)(x-2), 求m的值解:由题意得: 2x2+mx-2= (2x+1)(x-2)
∵ 2x2+mx-2=2x2-3x-2∴对应项的系数相等,则 m=-3会了吗? 请试一试若能x2+ax+b分解成(x+3)(x+4),求a,b的值比一比 赛一赛 谁最快?口答:1.(7.5)2-(0.5)2=( )
2.5732-4272=( )56146000看一看 想一想
你会吗?前后四位同学讨论已知: (1).若a+ b=7, b-a=3/7
求a2-b2的值(2).若a+ b=1, a-2b=3
求a2-ab-2b2的值 填空:
(1) 若x2+mx-n能分解成(x-2)(x-5),则 m= , n= 。-7-10(2)若x2-3x+m=(x-2)(??? ), 则
m=????????????x-121+x+x(1+x)=(1+x)+x(1+x)
=(1+x)(1+x)=(1+x)2从而1+x+x(1+x)+x (1+x)2= (1+x)2 +x (1+ x)2
= (1+x)2 (1+x)= (1+x)3 请仔细观察:从上面的因式分解中,你发现什么规律了吗?由此你能分解下列多项式吗?猜一猜,试一试!1) 1+x+x(1+x)+x (1+x)2 +x (1+x)3+x (1+x)42) 1+x+x(1+x)+x (1+x)2 +…+ x (1+x)n 提高题 如图是由2个边长分别为100和99的正方形重叠得到的.求图中蓝色部分的面积.…探索求新:图中若由100个边长分别为100,99,98,…,2,1的正方形重叠而成的,那么,按这种方式重叠而成的蓝色部分面积是________. 1002 –992 + 982- 972 +
962-952 +…+ 22-12
( ) ( )
( ) ( )=(100+99)(100-99)+(98+97)(98-97)
+(96+95)(96-95)+…+(2+1)(2-1)
=100+99+98+97+96+95+…+1=50505050探究活动:(画出草图,标明长度即可)现有2个面积为a2, 1个面积为b2的正方形和3个面积为ab的长方形,请你们用这些图形拼成一个新的长方形,并根据图形的面积,因式分解 2a2 +3ab+ b2。aaabbb 在日常生活中如取款、上网等都需 要密码,有一种用“因式分解”法产生的密码,方便记忆。原理:如对于多项式x3y2+6xy3因式分解的结果是xy2 (x2+6y),若取x=9,y=9时,x=9,y2=81,x2+6y=135.于是可以把“981135”作为一个密码。对于多项式3x2y+2xy2,取x=10,y=8, 用上述方法产生的密码是________。生活常识3680再 见
它们有什么不同的特点 .左边是右边是因此我们把左边这种变形叫做整式的乘法
右边这种变形叫做多项式的因式分解因式分解计算下列各式:做一做 比一比:整式乘法因式分解与整式乘法的关系 说明:
从左到右是因式分解,其特点是:由和差形式(多项式)转化成整式的积的形式;
从右到左是整式乘法,其特点是:由整式积的形式转化成和差形式(多项式). 结论:因式分解与整式乘法是互逆的关系. 因式分解
a2-b2 (a+b)(a-b)
整式乘法根据图形信息写出一个因式分解的式子aaba(1)因式分解: = ;a2+abbb(2)因式分解: = ;a2+2ab+b2(a+b)2a(a+b)abaabba-ba-b(3)因式分解: = ;a2-b2(a+b)(a-b)a(b+c+d)=ab+ac+ad观察下式结构特点得概念多项式的因式分解的定义把一个多项式化成几个整式积的形式叫做多项式的因式分解整式的积多项式练习一 理解概念判断下列各式哪些是整式乘法?哪些是因式分解?
(1).x2-4y2=(x+2y)(x-2y)
(2).2x(x-3y)=2x2-6xy
(3).(5a-1)2=25a2-10a+1
(4).x2+4x+4=(x+2)2
(5).(a-3)(a+3)=a2-9
(6).m2-4=(m+4)(m-4)
(7).2 πR+ 2 πr= 2 π(R+r)因式分解整式乘法整式乘法因式分解整式乘法不是因式分解因式分解辨一辨(1)(2)(3)(4)(5)(6)(7)是不是不是不是不是不是不是下列代数式从左到右的变形是因式分解吗?因式分解: 把一个多项式转化成几个整式
的积的形式.X-4= (x≥0)是因式分解吗?(1)因式分解是对
多项式而言的一种变形;
(2)因式分解的结果
仍是几个整式的积的形式; 再来辨一辨 以上都不是因式分解填空:(1)∵m(a+b)=ma+mb
∴ma+mb= ( )( );
(2)∵(a+4)(a-3) = a2+a-12
∴a2+a-12 = ( )( );m a+ba+4 a-3 你能利用因式分解与整式乘法之间的关系,举出几个因式分解的例子吗?连一连: 试一试 你能用几种不同的方法计算 10032-10022,哪种方法最简单? 10032-10022 =(1003+1002)(1003-1002) =2005×1 =2005看谁算得快(1)若a=1001,b=999,则a2-b2=___________;
(2)若a=99,b=-1,则a2-2ab+b2=_______;
(3)若x=-3,则20x2+60x=____________。
(1)a2-b2=(a+b)(a-b)=(1001+999)(1001-999)=4000(2)a2-2ab+b2=(a-b) 2=(99+1)2 =10000(3)20x2+60x= 20x(x+3)= 20× (-3)(-3+3)=0。4000100000 小结 因式分解学习目标1.理解因式分解的概念2.会判定一个从左到右的恒等变形是不是因式分解3.学会运用因式分解的方法来解题重点:理解因式分解的概念难点:理解因式分解与整式乘法的相互关系,
并运用它们之间的相互关系寻找因式分解的方法关键点:会判定一个从左到右的恒等变形是不是因式
分 解的关键:左边必须是多项式,右边是几
个整式的积
慈溪江滨公园修建了三块长方形的绿化草坪,它们的宽都是8㎝,长分别是55.5㎝,24.4㎝,20.1㎝,那么这些绿化带的面积之和是多少? 855.5+24.4+20.1=100你能解决吗?8×55.5+8×24.4+8×20.1
=8×(55.5+24.4+20.1)(1)若(a+5)(a+2)=a2+7a+10, (2)若 x2+mx-n能分解成(x-2)(x-5), 新知知多少则a2+7a+10=( )( )则m=____,n=____.(3)若x2-6x+m=(x-4)(x-2 ),
则m=____。8 993-99能被100整除吗?你是怎样想的? 与同伴交流. 小明是这样想的:
993-99=99×992-99 ×1
=99 ×(992-1)
=99 (99+1)(99-1)
= 99×100×98
所以, 993-99能被100整除.
你知道每一步的根据吗?
想一想: 993-99还能被哪些整数整除?想一想?智力抢答(1)1012-992=(2)872+87×13=(3)512-2×51+1=(4)20102-2010×2009=真厉害!400870025002010再想一想?如果2x2+mx-2可分解因式为
(2x+1)(x-2), 求m的值解:由题意得: 2x2+mx-2= (2x+1)(x-2)
∵ 2x2+mx-2=2x2-3x-2∴对应项的系数相等,则 m=-3会了吗? 请试一试若能x2+ax+b分解成(x+3)(x+4),求a,b的值比一比 赛一赛 谁最快?口答:1.(7.5)2-(0.5)2=( )
2.5732-4272=( )56146000看一看 想一想
你会吗?前后四位同学讨论已知: (1).若a+ b=7, b-a=3/7
求a2-b2的值(2).若a+ b=1, a-2b=3
求a2-ab-2b2的值 填空:
(1) 若x2+mx-n能分解成(x-2)(x-5),则 m= , n= 。-7-10(2)若x2-3x+m=(x-2)(??? ), 则
m=????????????x-121+x+x(1+x)=(1+x)+x(1+x)
=(1+x)(1+x)=(1+x)2从而1+x+x(1+x)+x (1+x)2= (1+x)2 +x (1+ x)2
= (1+x)2 (1+x)= (1+x)3 请仔细观察:从上面的因式分解中,你发现什么规律了吗?由此你能分解下列多项式吗?猜一猜,试一试!1) 1+x+x(1+x)+x (1+x)2 +x (1+x)3+x (1+x)42) 1+x+x(1+x)+x (1+x)2 +…+ x (1+x)n 提高题 如图是由2个边长分别为100和99的正方形重叠得到的.求图中蓝色部分的面积.…探索求新:图中若由100个边长分别为100,99,98,…,2,1的正方形重叠而成的,那么,按这种方式重叠而成的蓝色部分面积是________. 1002 –992 + 982- 972 +
962-952 +…+ 22-12
( ) ( )
( ) ( )=(100+99)(100-99)+(98+97)(98-97)
+(96+95)(96-95)+…+(2+1)(2-1)
=100+99+98+97+96+95+…+1=50505050探究活动:(画出草图,标明长度即可)现有2个面积为a2, 1个面积为b2的正方形和3个面积为ab的长方形,请你们用这些图形拼成一个新的长方形,并根据图形的面积,因式分解 2a2 +3ab+ b2。aaabbb 在日常生活中如取款、上网等都需 要密码,有一种用“因式分解”法产生的密码,方便记忆。原理:如对于多项式x3y2+6xy3因式分解的结果是xy2 (x2+6y),若取x=9,y=9时,x=9,y2=81,x2+6y=135.于是可以把“981135”作为一个密码。对于多项式3x2y+2xy2,取x=10,y=8, 用上述方法产生的密码是________。生活常识3680再 见
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
