浙教版数学七年级下册同步课件:1.3平行线的判定(2)(共17张PPT)
文档属性
| 名称 | 浙教版数学七年级下册同步课件:1.3平行线的判定(2)(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-17 14:27:19 | ||
图片预览




文档简介
(共17张PPT)
第一章 平行线
1.3 平行线的判定(2)
如何判断两条直线平行?
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
在同一平面内,垂直于同一条直线的两条直线互相平行.
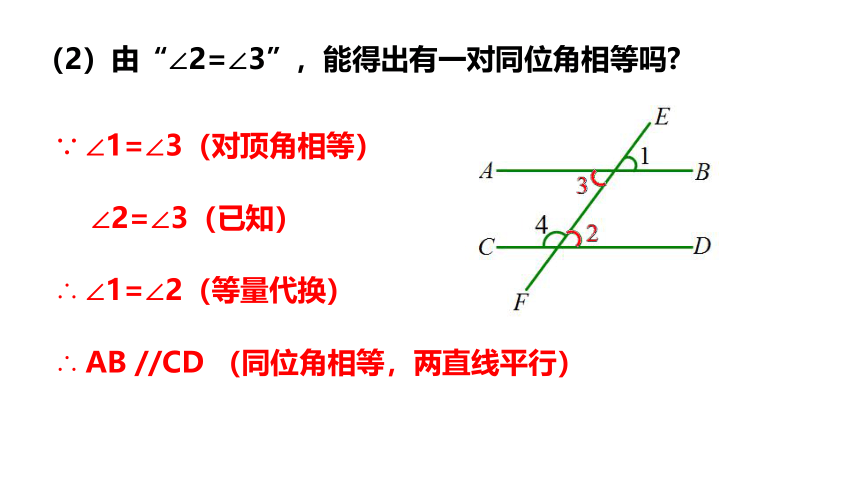
探究1:如图所示,直线AB,CD 被直线EF 所截. 若∠2=∠3,则AB 与CD 平行吗
(1)上节课,我们已经有怎样的判定两直线平行的方法?
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
(2)由“∠2=∠3”,能得出有一对同位角相等吗
∵ ∠1=∠3(对顶角相等)
∠2=∠3(已知)
∴ ∠1=∠2(等量代换)
∴ AB //CD (同位角相等,两直线平行)
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
内错角相等,两直线平行
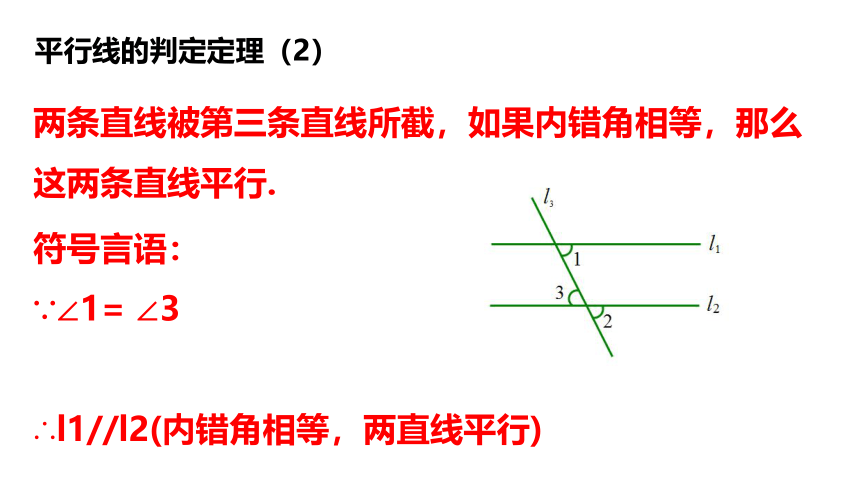
平行线的判定定理(2)
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
符号言语:
∵∠1= ∠3
∴l1//l2(内错角相等,两直线平行)
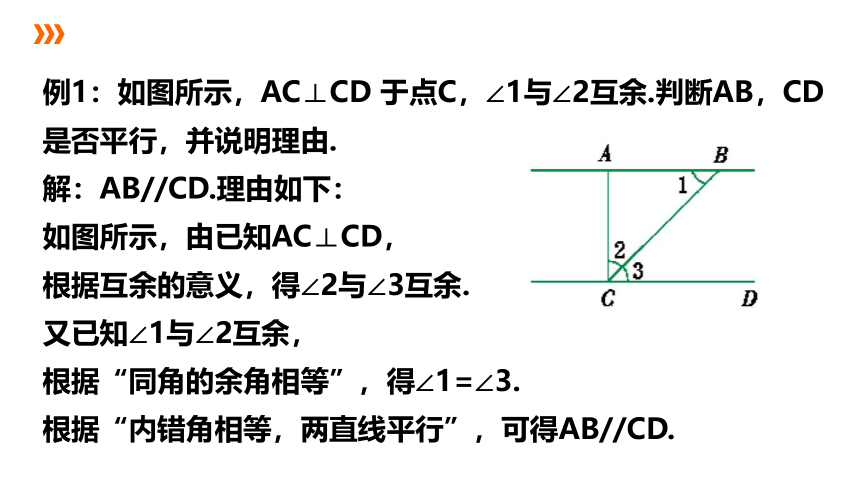
例1:如图所示,AC⊥CD 于点C,∠1与∠2互余.判断AB,CD 是否平行,并说明理由.
解:AB//CD.理由如下:
如图所示,由已知AC⊥CD,
根据互余的意义,得∠2与∠3互余.
又已知∠1与∠2互余,
根据“同角的余角相等”,得∠1=∠3.
根据“内错角相等,两直线平行”,可得AB//CD.
如图所示,直线AB,CD 被直线EF 所截. 若∠3+∠4=180 ° ,易知AB 与CD 平行. 想一想,为什么
∵ ∠2+∠4=180 ° (平角定义)
∠3+∠4=180 ° (已知)
∴ ∠2=∠3(等量代换)
∴ AB //CD (内错角相等,两直线平行)
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
同旁内角互补,两直线平行
平行线的判定定理(3)
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
符号言语:
∵∠1+∠4=180 °
∴l1//l2(同旁内角互补,两直线平行)
判定两直线平行的方法
(1)当已知两条直线的交点个数,可用定义法判定;
(2)当待判定的两条直线与第三条直线相交,可抓住所成角的位置与特殊性判定:①同位角相等,两直线平行;②内错角相等,两直线平行;③同旁内角互补,两直线平行;
(3)若两条直线在同一平面内都垂直于第三条直线,则可用“在同一平面内,垂直于同一条直线的两条直线互相平行”来判定.
例2:如图所示,AP 平分∠BAC,CP 平分∠ACD,∠1+∠2=90°.判断AB,CD 是否平行,并说明理由.
解:AB//CD.理由如下:
已知AP 平分∠BAC,CP 平分∠ACD,
根据角平分线的意义,知
∠1= ∠BAC, ∠2= ∠ACD,
∴ ∠BAC+∠ACD=2(∠1+∠2)=2×90°=180°.
根据“同旁内角互补,两直线平行”,得AB//CD.
平行线的判定
同位角相等,两直线平行
内错角_______,两直线平行
同旁内角________,两直线平行
定义
相等
互补
1.[2019·嘉兴期末] 如图,若∠A=∠D,则AB∥CD,判断依据是( )
A.两直线平行,同位角相等 B.两直线平行,内错角相等
C.同位角相等,两直线平行 D.内错角相等,两直线平行
D
2.如图,若∠1=100°,∠4=80°,则 ∥ ,理由是 ;若∠3=70°,则∠2= °时,可推出AB∥CD.
AB
CD
同旁内角互补,两直线平行
110
3.如图1-3-20所示,AC⊥BC于点C,∠1与∠2互余.由这些条件能够判定哪两条直线平行 请说明理由.
[解析] 由垂直的定义可知∠ACB=90°,又知∠1与∠2互余,可得∠2与∠ACD互补,推出AB∥CD.
解:AB∥CD.理由如下:
因为AC⊥BC,所以∠ACB=90°.
因为∠1与∠2互余,所以∠1+∠2=90°,
所以∠2+∠ACB+∠1=180°,即∠2+∠ACD=180°,
所以AB∥CD(同旁内角互补,两直线平行).
第一章 平行线
1.3 平行线的判定(2)
如何判断两条直线平行?
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
在同一平面内,垂直于同一条直线的两条直线互相平行.
探究1:如图所示,直线AB,CD 被直线EF 所截. 若∠2=∠3,则AB 与CD 平行吗
(1)上节课,我们已经有怎样的判定两直线平行的方法?
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
(2)由“∠2=∠3”,能得出有一对同位角相等吗
∵ ∠1=∠3(对顶角相等)
∠2=∠3(已知)
∴ ∠1=∠2(等量代换)
∴ AB //CD (同位角相等,两直线平行)
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
内错角相等,两直线平行
平行线的判定定理(2)
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
符号言语:
∵∠1= ∠3
∴l1//l2(内错角相等,两直线平行)
例1:如图所示,AC⊥CD 于点C,∠1与∠2互余.判断AB,CD 是否平行,并说明理由.
解:AB//CD.理由如下:
如图所示,由已知AC⊥CD,
根据互余的意义,得∠2与∠3互余.
又已知∠1与∠2互余,
根据“同角的余角相等”,得∠1=∠3.
根据“内错角相等,两直线平行”,可得AB//CD.
如图所示,直线AB,CD 被直线EF 所截. 若∠3+∠4=180 ° ,易知AB 与CD 平行. 想一想,为什么
∵ ∠2+∠4=180 ° (平角定义)
∠3+∠4=180 ° (已知)
∴ ∠2=∠3(等量代换)
∴ AB //CD (内错角相等,两直线平行)
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
同旁内角互补,两直线平行
平行线的判定定理(3)
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
符号言语:
∵∠1+∠4=180 °
∴l1//l2(同旁内角互补,两直线平行)
判定两直线平行的方法
(1)当已知两条直线的交点个数,可用定义法判定;
(2)当待判定的两条直线与第三条直线相交,可抓住所成角的位置与特殊性判定:①同位角相等,两直线平行;②内错角相等,两直线平行;③同旁内角互补,两直线平行;
(3)若两条直线在同一平面内都垂直于第三条直线,则可用“在同一平面内,垂直于同一条直线的两条直线互相平行”来判定.
例2:如图所示,AP 平分∠BAC,CP 平分∠ACD,∠1+∠2=90°.判断AB,CD 是否平行,并说明理由.
解:AB//CD.理由如下:
已知AP 平分∠BAC,CP 平分∠ACD,
根据角平分线的意义,知
∠1= ∠BAC, ∠2= ∠ACD,
∴ ∠BAC+∠ACD=2(∠1+∠2)=2×90°=180°.
根据“同旁内角互补,两直线平行”,得AB//CD.
平行线的判定
同位角相等,两直线平行
内错角_______,两直线平行
同旁内角________,两直线平行
定义
相等
互补
1.[2019·嘉兴期末] 如图,若∠A=∠D,则AB∥CD,判断依据是( )
A.两直线平行,同位角相等 B.两直线平行,内错角相等
C.同位角相等,两直线平行 D.内错角相等,两直线平行
D
2.如图,若∠1=100°,∠4=80°,则 ∥ ,理由是 ;若∠3=70°,则∠2= °时,可推出AB∥CD.
AB
CD
同旁内角互补,两直线平行
110
3.如图1-3-20所示,AC⊥BC于点C,∠1与∠2互余.由这些条件能够判定哪两条直线平行 请说明理由.
[解析] 由垂直的定义可知∠ACB=90°,又知∠1与∠2互余,可得∠2与∠ACD互补,推出AB∥CD.
解:AB∥CD.理由如下:
因为AC⊥BC,所以∠ACB=90°.
因为∠1与∠2互余,所以∠1+∠2=90°,
所以∠2+∠ACB+∠1=180°,即∠2+∠ACD=180°,
所以AB∥CD(同旁内角互补,两直线平行).
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
