浙教版数学七年级下册同步课件:1.4平行线的性质(2)(共17张PPT)
文档属性
| 名称 | 浙教版数学七年级下册同步课件:1.4平行线的性质(2)(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 950.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 17:13:34 | ||
图片预览






文档简介
(共17张PPT)
第一章 平行线
1.4 平行线的性质(2)
回顾我们已经知道的平行线的性质
两条平行线被第三条直线所截,同位角相等. 简单地说:两直线平行,同位角相等.
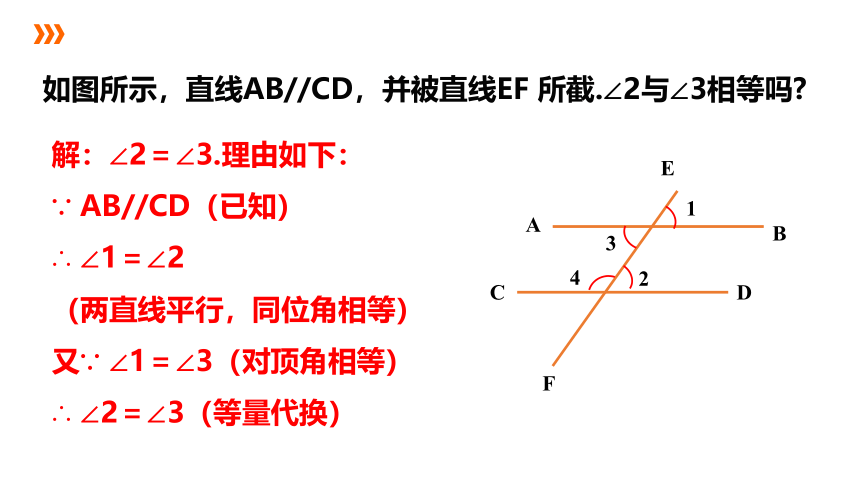
如图所示,直线AB//CD,并被直线EF 所截.∠2与∠3相等吗
1
E
B
D
F
A
C
3
4
2
解:∠2=∠3.理由如下:
∵ AB//CD(已知)
∴ ∠1=∠2
(两直线平行,同位角相等)
又∵ ∠1=∠3(对顶角相等)
∴ ∠2=∠3(等量代换)
两条平行线被第三条直线所截,内错角相等.
两直线平行,内错角相等
平行线的性质(2)
两条平行线被第三条直线所截,内错角相等.
简单地说:两直线平行,内错角相等.
符号言语:
∵l1//l2
∴ ∠1= ∠3 (两直线平行,内错角相等)
如图所示,直线AB//CD,并被直线EF 所截. ∠3与∠4的和是多少度
1
E
B
D
F
A
C
3
4
2
解:∠3+∠4=180°.理由如下:
∵ AB//CD(已知)
∴ ∠2=∠3
(两直线平行,内错角相等)
又∵ ∠2+∠4=180°(平角的意义)
∴ ∠3+∠4=180°.(等量代换)
两条平行线被第三条直线所截,同旁内角互补.
两直线平行,同旁内角互补
平行线的性质(3)
两条平行线被第三条直线所截,同旁内角互补.
简单地说:两直线平行,同旁内角互补.
符号言语:
∵l1//l2
∴ ∠1+ ∠ 4=180° (两直线平行,同旁内角互补)
平行线性质和判定的综合应用的“两点注意”
(1)在利用平行线的性质或判定时,一定要看清楚同位角、内错角、同旁内角是由哪两条直线被哪条直线所截而成的;
(2)搞清平行线的判定与性质的区别,由已知角的关系得平行时用判定,由已知平行的关系得角的关系时用性质.
做一做
如图所示,AB,CD被EF所截,AB//CD,∠1=120°.求∠2,∠3的大小(填空,并说明理由).
已知∠1=120°,
根据(__________________________)
则∠2=_______
根据(__________________________),
得∠3=_______-∠1=_______.
两直线平行,内错角相等
120°
两直线平行,同旁内角互补
180°
60°
D
C
A
B
1
2
E
F
3
例1:如图所示,已知AB//CD,AD//BC. 判断∠1与∠2是否相等,并说明理由.
解:∠1=∠2.理由如下:
已知AB//CD,
根据“两直线平行,同旁内角互补”,
得∠1+∠BAD=180°.
同理,由AD//BC,得∠2+∠BAD=180°.
根据“同角的补角相等”,得∠1=∠2.
D
C
A
B
1
2
例2:如图所示,已知∠ABC+∠C=180°,BD平分∠ABC. ∠CBD与∠D 相等吗 请说明理由.
解:∠CBD=∠D.理由如下:
∵ ∠ABC+∠C=180°.
根据“同旁内角互补,两直线平行”,
得AB//CD.
再根据“两直线平行,内错角相等”。
得∠D=∠ABD.
∵ BD平分∠ABC,
∴∠CBD=∠ABD.
∴∠CBD=∠D.
A
B
D
C
平行线的性质
两直线平行,同位角相等
两直线平行,内错角_______
两直线平行,同旁内角________
平行线的判定
相等
互补
1.如图,AB∥CD,直线l分别与AB,CD相交.若∠1=50°,则∠2的度数为 .
50°
2.如图所示,若AB∥CD,则下列式子正确的是 ( )
A.∠A+∠C=180°
B.∠B+∠A=180°
C.∠B+∠C=180°
D.∠B+∠D=180°
C
3.下列说法中正确的是 ( )
A.两直线被第三条直线所截得的同位角相等
B.两直线被第三条直线所截得的同旁内角互补
C.两平行线被第三条直线所截得的同位角的平分线互相垂直
D.两平行线被第三条直线所截得的同旁内角的平分线互相垂直
D
4.[2019·杭州下城区期中] 如图,∠1=80°,∠2=100°,∠3=76°,则∠4的度数为 °.
76
第一章 平行线
1.4 平行线的性质(2)
回顾我们已经知道的平行线的性质
两条平行线被第三条直线所截,同位角相等. 简单地说:两直线平行,同位角相等.
如图所示,直线AB//CD,并被直线EF 所截.∠2与∠3相等吗
1
E
B
D
F
A
C
3
4
2
解:∠2=∠3.理由如下:
∵ AB//CD(已知)
∴ ∠1=∠2
(两直线平行,同位角相等)
又∵ ∠1=∠3(对顶角相等)
∴ ∠2=∠3(等量代换)
两条平行线被第三条直线所截,内错角相等.
两直线平行,内错角相等
平行线的性质(2)
两条平行线被第三条直线所截,内错角相等.
简单地说:两直线平行,内错角相等.
符号言语:
∵l1//l2
∴ ∠1= ∠3 (两直线平行,内错角相等)
如图所示,直线AB//CD,并被直线EF 所截. ∠3与∠4的和是多少度
1
E
B
D
F
A
C
3
4
2
解:∠3+∠4=180°.理由如下:
∵ AB//CD(已知)
∴ ∠2=∠3
(两直线平行,内错角相等)
又∵ ∠2+∠4=180°(平角的意义)
∴ ∠3+∠4=180°.(等量代换)
两条平行线被第三条直线所截,同旁内角互补.
两直线平行,同旁内角互补
平行线的性质(3)
两条平行线被第三条直线所截,同旁内角互补.
简单地说:两直线平行,同旁内角互补.
符号言语:
∵l1//l2
∴ ∠1+ ∠ 4=180° (两直线平行,同旁内角互补)
平行线性质和判定的综合应用的“两点注意”
(1)在利用平行线的性质或判定时,一定要看清楚同位角、内错角、同旁内角是由哪两条直线被哪条直线所截而成的;
(2)搞清平行线的判定与性质的区别,由已知角的关系得平行时用判定,由已知平行的关系得角的关系时用性质.
做一做
如图所示,AB,CD被EF所截,AB//CD,∠1=120°.求∠2,∠3的大小(填空,并说明理由).
已知∠1=120°,
根据(__________________________)
则∠2=_______
根据(__________________________),
得∠3=_______-∠1=_______.
两直线平行,内错角相等
120°
两直线平行,同旁内角互补
180°
60°
D
C
A
B
1
2
E
F
3
例1:如图所示,已知AB//CD,AD//BC. 判断∠1与∠2是否相等,并说明理由.
解:∠1=∠2.理由如下:
已知AB//CD,
根据“两直线平行,同旁内角互补”,
得∠1+∠BAD=180°.
同理,由AD//BC,得∠2+∠BAD=180°.
根据“同角的补角相等”,得∠1=∠2.
D
C
A
B
1
2
例2:如图所示,已知∠ABC+∠C=180°,BD平分∠ABC. ∠CBD与∠D 相等吗 请说明理由.
解:∠CBD=∠D.理由如下:
∵ ∠ABC+∠C=180°.
根据“同旁内角互补,两直线平行”,
得AB//CD.
再根据“两直线平行,内错角相等”。
得∠D=∠ABD.
∵ BD平分∠ABC,
∴∠CBD=∠ABD.
∴∠CBD=∠D.
A
B
D
C
平行线的性质
两直线平行,同位角相等
两直线平行,内错角_______
两直线平行,同旁内角________
平行线的判定
相等
互补
1.如图,AB∥CD,直线l分别与AB,CD相交.若∠1=50°,则∠2的度数为 .
50°
2.如图所示,若AB∥CD,则下列式子正确的是 ( )
A.∠A+∠C=180°
B.∠B+∠A=180°
C.∠B+∠C=180°
D.∠B+∠D=180°
C
3.下列说法中正确的是 ( )
A.两直线被第三条直线所截得的同位角相等
B.两直线被第三条直线所截得的同旁内角互补
C.两平行线被第三条直线所截得的同位角的平分线互相垂直
D.两平行线被第三条直线所截得的同旁内角的平分线互相垂直
D
4.[2019·杭州下城区期中] 如图,∠1=80°,∠2=100°,∠3=76°,则∠4的度数为 °.
76
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
