浙教版七年级下册3.3多项式的乘法 (1)课件(共18张PPT)
文档属性
| 名称 | 浙教版七年级下册3.3多项式的乘法 (1)课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 08:35:35 | ||
图片预览




文档简介
(共18张PPT)
第三章 整式的乘除
3.3 多项式的乘法(1)
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加
人们越来越重视厨房的设计, 不少家庭的厨房会沿墙做一排矮柜,使厨房的空间得到充分利用,而且便于清理.
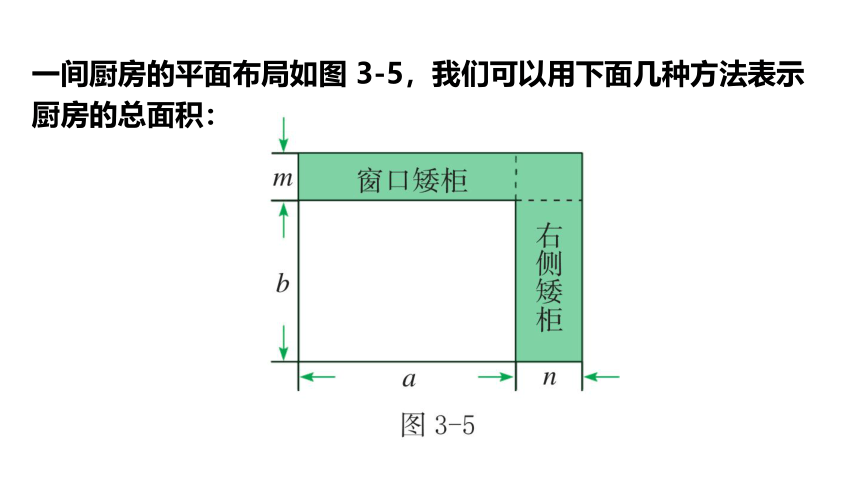
一间厨房的平面布局如图 3-5,我们可以用下面几种方法表示厨房的总面积:
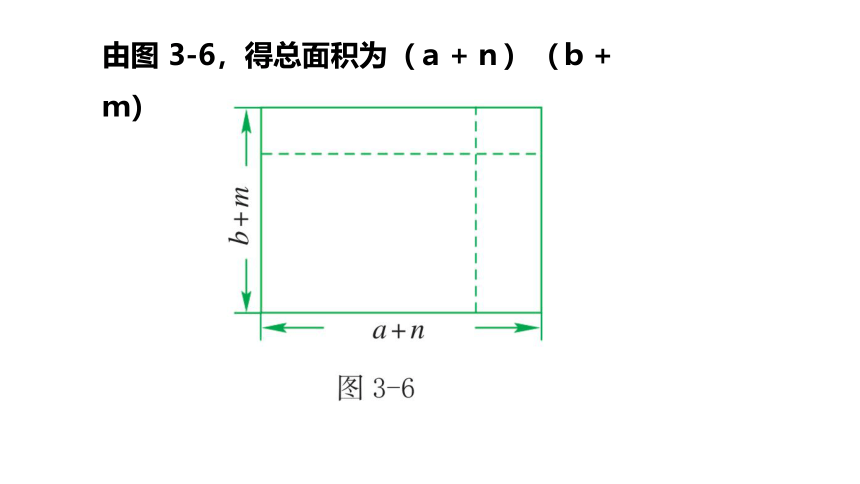
由图 3-6,得总面积为(a+n)(b+m)
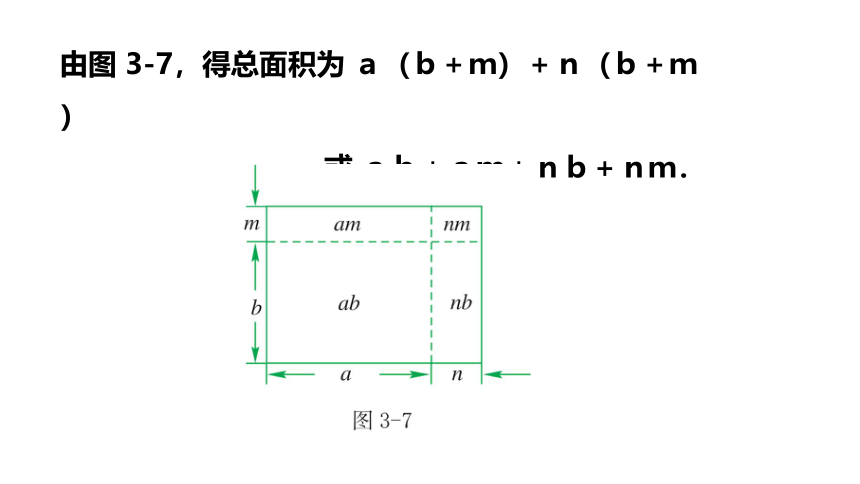
由图 3-7,得总面积为 a(b+m)+n(b+m)
或 ab+am+nb+nm.
由此,可以得到:
(a+n)(b+m)
=a(b+m)+n(b+m)
=ab+am+nb+nm.
一般地,多项式与多项式相乘有下面的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
1
2
3
4
(a+n)(b+m)
=
ab
1
2
3
4
+am
+nb
+nm
例 1 计算:
(1)(x+y)(a+2b). (2)(3x-1)(x+3).
解 (1)(x+y)(a+2b)
=x·a+x·(2b)+y·a+y·(2b)
=ax+2bx+ay+2by.
(2)(3x-1)(x+3)
=3x 2 +9x-x-3
=3x 2 +8x-3.
例2 先化简,再求值:
(2a-3)(3a+1)-6a(a-4),其 中 a= .
解 (2a-3)(3a+1)-6a(a-4)
=6a2 +2a-9a-3-6a2 +2 4a
=17a-3.
当 a= 时,原式=1 7× -3=-1.
多项式乘多项式的“三点注意”
(1)相乘时,按一定的顺序进行,必须做到不重不漏;
(2)多项式与多项式相乘,仍得多项式,在合并同类项之前,积的项数等于原多项式的项数之积;
(3)相乘后,若有同类项,则应把同类项合并.
化简求值
法则:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积_____,即(a+n)(b+m) = ______________________
多项式的乘法
多项式乘多项式的应用
相加
ab+am+nb+nm
多项式乘多项式的计算
1.[2019·台湾] 下列式子中与(2x-3)(3x+4)的计算结果相同的是 ( )
A.-7x+4 B.-7x-12
C.6x2-12 D.6x2-x-12
2.下列各式中,计算结果是x2+7x-18的是 ( )
A.(x-1)(x+18) B.(x+2)(x+9)
C.(x-3)(x+6) D.(x-2)(x+9)
D
D
3.计算:
(1)(x-2)(x+3); (2)(x+3)(3x-2);
解:(1)(x-2)(x+3)=x2+3x-2x-6=x2+x-6.
(2)原式=3x2-2x+9x-6=3x2+7x-6.
4.如图,在某住房小区的建设中,为了提高业主的居住环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.问剩余草坪的面积是多少平方米.
解:如图所示.
图中空白部分的面积即为剩余草坪的面积.
空白部分的面积为
(4a+3b-b)(2a+3b-b)
=(4a+2b)(2a+2b)
=8a2+8ab+4ab+4b2
=8a2+12ab+4b2(平方米).
答:剩余草坪的面积是(8a2+12ab+4b2)平方米.
第三章 整式的乘除
3.3 多项式的乘法(1)
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式
单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加
人们越来越重视厨房的设计, 不少家庭的厨房会沿墙做一排矮柜,使厨房的空间得到充分利用,而且便于清理.
一间厨房的平面布局如图 3-5,我们可以用下面几种方法表示厨房的总面积:
由图 3-6,得总面积为(a+n)(b+m)
由图 3-7,得总面积为 a(b+m)+n(b+m)
或 ab+am+nb+nm.
由此,可以得到:
(a+n)(b+m)
=a(b+m)+n(b+m)
=ab+am+nb+nm.
一般地,多项式与多项式相乘有下面的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
1
2
3
4
(a+n)(b+m)
=
ab
1
2
3
4
+am
+nb
+nm
例 1 计算:
(1)(x+y)(a+2b). (2)(3x-1)(x+3).
解 (1)(x+y)(a+2b)
=x·a+x·(2b)+y·a+y·(2b)
=ax+2bx+ay+2by.
(2)(3x-1)(x+3)
=3x 2 +9x-x-3
=3x 2 +8x-3.
例2 先化简,再求值:
(2a-3)(3a+1)-6a(a-4),其 中 a= .
解 (2a-3)(3a+1)-6a(a-4)
=6a2 +2a-9a-3-6a2 +2 4a
=17a-3.
当 a= 时,原式=1 7× -3=-1.
多项式乘多项式的“三点注意”
(1)相乘时,按一定的顺序进行,必须做到不重不漏;
(2)多项式与多项式相乘,仍得多项式,在合并同类项之前,积的项数等于原多项式的项数之积;
(3)相乘后,若有同类项,则应把同类项合并.
化简求值
法则:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积_____,即(a+n)(b+m) = ______________________
多项式的乘法
多项式乘多项式的应用
相加
ab+am+nb+nm
多项式乘多项式的计算
1.[2019·台湾] 下列式子中与(2x-3)(3x+4)的计算结果相同的是 ( )
A.-7x+4 B.-7x-12
C.6x2-12 D.6x2-x-12
2.下列各式中,计算结果是x2+7x-18的是 ( )
A.(x-1)(x+18) B.(x+2)(x+9)
C.(x-3)(x+6) D.(x-2)(x+9)
D
D
3.计算:
(1)(x-2)(x+3); (2)(x+3)(3x-2);
解:(1)(x-2)(x+3)=x2+3x-2x-6=x2+x-6.
(2)原式=3x2-2x+9x-6=3x2+7x-6.
4.如图,在某住房小区的建设中,为了提高业主的居住环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.问剩余草坪的面积是多少平方米.
解:如图所示.
图中空白部分的面积即为剩余草坪的面积.
空白部分的面积为
(4a+3b-b)(2a+3b-b)
=(4a+2b)(2a+2b)
=8a2+8ab+4ab+4b2
=8a2+12ab+4b2(平方米).
答:剩余草坪的面积是(8a2+12ab+4b2)平方米.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
