浙教版数学七年级下册 3.4乘法公式(1)同步课件(共17张PPT)
文档属性
| 名称 | 浙教版数学七年级下册 3.4乘法公式(1)同步课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 945.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第三章 整式的乘除
3.4 乘法公式(1)
前边我们学习了整式的乘法,知道了多项式与多项式相乘的法则.根据所学知识,计算下列多项式的积,你能发现什么规律?
(1)(x+1)(x-1)=_____________________
(2)(m+2)(m-2)=_____________________
(3)(2x+1)(2x-1)=_____________________
x2-1
m2-4
4x2-1
请计算:(a+b)(a-b)=__________ .
比较等号两边的代数式,它们在系数和字母方面各有什么特点?
a2-b2
想一想,除了计算,我们还有什么办法证明?
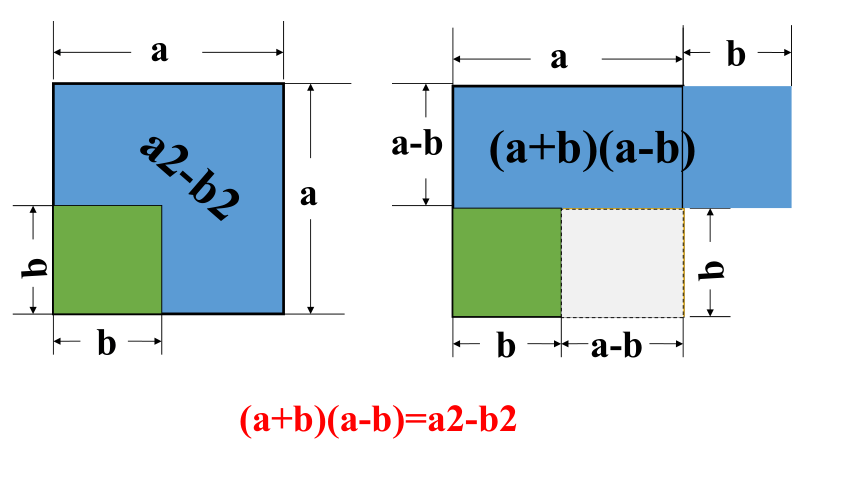
利用图形的面积
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)=a2-b2
a-b
a-b
(a+b)(a-b)
(a+b)(a b)=
a2 b2
两数和与这两数差的积,等于这两数的平方差.
平方差公式
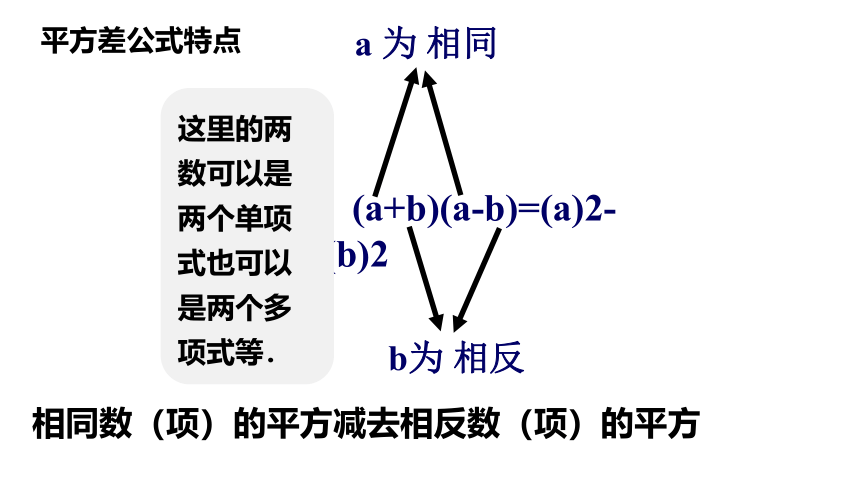
(a+b)(a-b)=(a)2-(b)2
b为 相反
a 为 相同
平方差公式特点
相同数(项)的平方减去相反数(项)的平方
这里的两数可以是两个单项式也可以是两个多项式等.
平方差公式的结构特点
1.等号左边:
(1)两个二项式的积;
(2)两个二项式中有相同项和相反项.
2.等号右边:
(1)二项式;
(2)相同项的平方减去相反项的平方.
(1)(-a+b)(a+b)= _________
(2)(a-b)(b+a)= __________
(3)(-a-b)(-a+b)= ________
(4)(a-b)(-a-b)= _________
a2-b2
a2-b2
b2-a2
b2-a2
参照平方差公式“(a+b)(a-b)=a2-b2”填空。
例1 运用平方差公式计算:
(1)(3x+5y)(3x-5y).
(2)
解 (1)(3x+5y)(3x-5y)
=(3x)2-(5y)2
=9x2-25y2
(2)
例2 用平方差公式计算:
(1) 103×97 (2) 59.8×60.2
解:(1) 103×97
=(100+3)(100-3)
=1002-32
=10000-9
=9991
(2) 59.8×60.2
=(60-0.2)(60+0.2)
=602-0.22
=3600-0.04
=3599.96
两数和与这两数差的积等于这两数的_______.即(_____)·( _____)=_______
平方差公式
化简
计算
应用
平方差
a+b
a-b
a2-b2
1.[2019·嵊州期中] 下列各式不能使用平方差公式的是 ( )
A.(2a+3b)(2a-3b)
B.(-2a+3b)(3b-2a)
C.(-2a+3b)(-2a-3b)
D.(2a-3b)(-2a-3b)
B
2.运用平方差公式计算:
(1)(3x-2)(3x+2); (2)(a+3b)(a-3b);
解:(1)原式=(3x)2-22=9x2-4.
(2)a2-9b2.
3.用简便方法计算:
(1)99.9×100.1; (2)31×29;
(1)9999.99
(2)899
4.某学校要改造一个边长为5x米的正方形花坛.现规划南北方向要缩短3米,东西方向要加长3米,则改造后花坛的面积是多少平方米 改造后花坛的面积增大或减少了多少平方米
解:根据题意得改造后花坛为长方形,
其长为(5x+3)米,宽为(5x-3)米,
所以长方形花坛的面积为(5x+3)(5x-3)=(25x2-9)平方米,
而原正方形花坛的面积为(5x)2=25x2(平方米),
所以改造后花坛的面积减少了9平方米.
第三章 整式的乘除
3.4 乘法公式(1)
前边我们学习了整式的乘法,知道了多项式与多项式相乘的法则.根据所学知识,计算下列多项式的积,你能发现什么规律?
(1)(x+1)(x-1)=_____________________
(2)(m+2)(m-2)=_____________________
(3)(2x+1)(2x-1)=_____________________
x2-1
m2-4
4x2-1
请计算:(a+b)(a-b)=__________ .
比较等号两边的代数式,它们在系数和字母方面各有什么特点?
a2-b2
想一想,除了计算,我们还有什么办法证明?
利用图形的面积
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)=a2-b2
a-b
a-b
(a+b)(a-b)
(a+b)(a b)=
a2 b2
两数和与这两数差的积,等于这两数的平方差.
平方差公式
(a+b)(a-b)=(a)2-(b)2
b为 相反
a 为 相同
平方差公式特点
相同数(项)的平方减去相反数(项)的平方
这里的两数可以是两个单项式也可以是两个多项式等.
平方差公式的结构特点
1.等号左边:
(1)两个二项式的积;
(2)两个二项式中有相同项和相反项.
2.等号右边:
(1)二项式;
(2)相同项的平方减去相反项的平方.
(1)(-a+b)(a+b)= _________
(2)(a-b)(b+a)= __________
(3)(-a-b)(-a+b)= ________
(4)(a-b)(-a-b)= _________
a2-b2
a2-b2
b2-a2
b2-a2
参照平方差公式“(a+b)(a-b)=a2-b2”填空。
例1 运用平方差公式计算:
(1)(3x+5y)(3x-5y).
(2)
解 (1)(3x+5y)(3x-5y)
=(3x)2-(5y)2
=9x2-25y2
(2)
例2 用平方差公式计算:
(1) 103×97 (2) 59.8×60.2
解:(1) 103×97
=(100+3)(100-3)
=1002-32
=10000-9
=9991
(2) 59.8×60.2
=(60-0.2)(60+0.2)
=602-0.22
=3600-0.04
=3599.96
两数和与这两数差的积等于这两数的_______.即(_____)·( _____)=_______
平方差公式
化简
计算
应用
平方差
a+b
a-b
a2-b2
1.[2019·嵊州期中] 下列各式不能使用平方差公式的是 ( )
A.(2a+3b)(2a-3b)
B.(-2a+3b)(3b-2a)
C.(-2a+3b)(-2a-3b)
D.(2a-3b)(-2a-3b)
B
2.运用平方差公式计算:
(1)(3x-2)(3x+2); (2)(a+3b)(a-3b);
解:(1)原式=(3x)2-22=9x2-4.
(2)a2-9b2.
3.用简便方法计算:
(1)99.9×100.1; (2)31×29;
(1)9999.99
(2)899
4.某学校要改造一个边长为5x米的正方形花坛.现规划南北方向要缩短3米,东西方向要加长3米,则改造后花坛的面积是多少平方米 改造后花坛的面积增大或减少了多少平方米
解:根据题意得改造后花坛为长方形,
其长为(5x+3)米,宽为(5x-3)米,
所以长方形花坛的面积为(5x+3)(5x-3)=(25x2-9)平方米,
而原正方形花坛的面积为(5x)2=25x2(平方米),
所以改造后花坛的面积减少了9平方米.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
