浙教版数学七年级下册 3.4 乘法公式(1) 课件(共17张PPT)
文档属性
| 名称 | 浙教版数学七年级下册 3.4 乘法公式(1) 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 371.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-11 11:50:17 | ||
图片预览






文档简介
(共17张PPT)
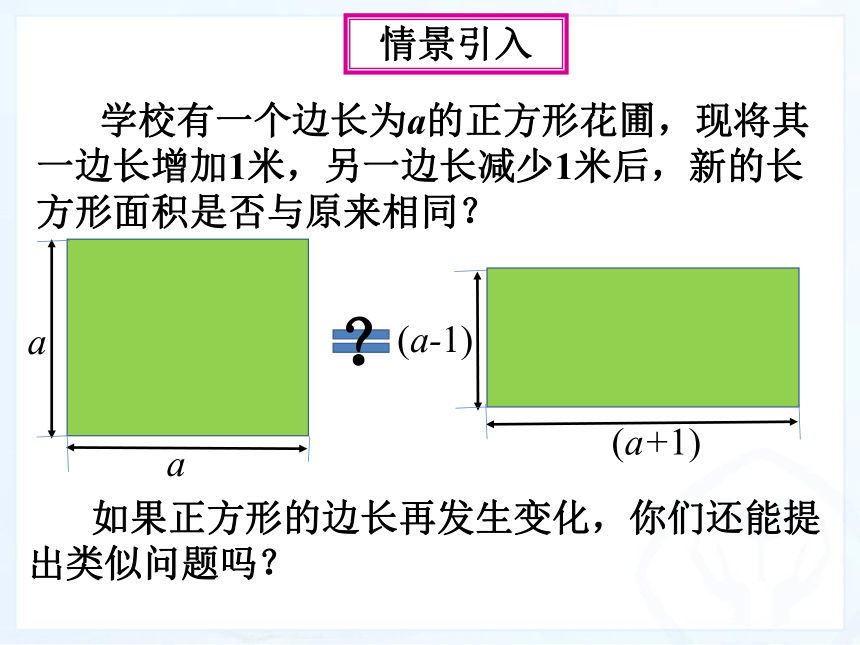
平方差公式
学校有一个边长为a的正方形花圃,现将其一边长增加1米,另一边长减少1米后,新的长方形面积是否与原来相同?
情景引入
a
a
(a+1)
(a-1)
?
如果正方形的边长再发生变化,你们还能提出类似问题吗?
探究公式
你能发现怎样的结论?试着说一说.
猜想公式
我发现:
请将你的发现用字母表示出来.
你能对所发现的结论进行验证吗?
验证公式——代数法
(a+b)(a-b)=a2-ab+ab-b2
=a2-b2
平方差公式表述
符号表示:
两个数的和与这两个数的差的积,等于这两个数的平方差.
语言表述:
理解平方差公式
下列两个多项式相乘 ,哪些可用平方差公式?哪些不能?
(1)(x+2)(x+2); (2)(x-3)(x-3);
(3)(x+3)(x-4); (4)(x+y)(x-y).
×
×
×
√
=x2-y2
公式特征:公式中,
(1) ——相当于公式中的“a”,
——相当于公式中的“b”.
(2)符合平方差公式特征的式子都可以直接写出运算结果,即:
一部分完全相同
另一部分只有符号不同
完全相同部分2-只有符号不同部分2.
验证平方差公式——几何法
(a+b)(a-b)
a2-b2
=
请思考:
其实,公式中的字母a,b可以是具体的数、单项式或多项式.
理解平方差公式
解:
=
一定要分清“a”和“b”哟
解:(1)原式=(3x+2)(3x-2)=(3x)2-22=9x2-4
理解平方差公式
变式练习
计算:(1)(3x+2)(-2+3x); (2)(-x+2y)(x+2y).
(2)原式=(2y-x)(2y+x)=(2y)2-x2=4y2-x2
有时需要先把不符合公式标准形式的题目加以调整,再运用公式.
巩固平方差公式
应用二:“自编题”活动
要求:
(1)请同学们各自编写两道符合平方差公式特征的整式乘法.
(2)将所编制的题目在小组交流,并完成计算.
(3)各组选派代表将所出题在全班进行交流.
运用平方差公式
只有符合公式条件的乘法,才能运用公式简化运算,其余的运算仍按乘法法则进行.
连续套用平方差公式哟!
当堂小结
请你说说看:通过今天的学习,你学会了什么?还有什么疑惑?
观察特例猜想公式
特殊 一般
特殊
1.主要知识:
2.基本思想:
当堂小结
数形结合的思想
用代数法
验证公式
几何图形
验证公式
运用公式
解决问题
转化的思想
当堂小结
3.前后知识的联系:
(a+b) =a +a +b +b
( + )
m
n
m
n
m
n
·a
·(-b)
a
(-b)
[ + ]
·(-b)
·a
=a2-b2
当堂测试
拓展训练
平方差公式
学校有一个边长为a的正方形花圃,现将其一边长增加1米,另一边长减少1米后,新的长方形面积是否与原来相同?
情景引入
a
a
(a+1)
(a-1)
?
如果正方形的边长再发生变化,你们还能提出类似问题吗?
探究公式
你能发现怎样的结论?试着说一说.
猜想公式
我发现:
请将你的发现用字母表示出来.
你能对所发现的结论进行验证吗?
验证公式——代数法
(a+b)(a-b)=a2-ab+ab-b2
=a2-b2
平方差公式表述
符号表示:
两个数的和与这两个数的差的积,等于这两个数的平方差.
语言表述:
理解平方差公式
下列两个多项式相乘 ,哪些可用平方差公式?哪些不能?
(1)(x+2)(x+2); (2)(x-3)(x-3);
(3)(x+3)(x-4); (4)(x+y)(x-y).
×
×
×
√
=x2-y2
公式特征:公式中,
(1) ——相当于公式中的“a”,
——相当于公式中的“b”.
(2)符合平方差公式特征的式子都可以直接写出运算结果,即:
一部分完全相同
另一部分只有符号不同
完全相同部分2-只有符号不同部分2.
验证平方差公式——几何法
(a+b)(a-b)
a2-b2
=
请思考:
其实,公式中的字母a,b可以是具体的数、单项式或多项式.
理解平方差公式
解:
=
一定要分清“a”和“b”哟
解:(1)原式=(3x+2)(3x-2)=(3x)2-22=9x2-4
理解平方差公式
变式练习
计算:(1)(3x+2)(-2+3x); (2)(-x+2y)(x+2y).
(2)原式=(2y-x)(2y+x)=(2y)2-x2=4y2-x2
有时需要先把不符合公式标准形式的题目加以调整,再运用公式.
巩固平方差公式
应用二:“自编题”活动
要求:
(1)请同学们各自编写两道符合平方差公式特征的整式乘法.
(2)将所编制的题目在小组交流,并完成计算.
(3)各组选派代表将所出题在全班进行交流.
运用平方差公式
只有符合公式条件的乘法,才能运用公式简化运算,其余的运算仍按乘法法则进行.
连续套用平方差公式哟!
当堂小结
请你说说看:通过今天的学习,你学会了什么?还有什么疑惑?
观察特例猜想公式
特殊 一般
特殊
1.主要知识:
2.基本思想:
当堂小结
数形结合的思想
用代数法
验证公式
几何图形
验证公式
运用公式
解决问题
转化的思想
当堂小结
3.前后知识的联系:
(a+b) =a +a +b +b
( + )
m
n
m
n
m
n
·a
·(-b)
a
(-b)
[ + ]
·(-b)
·a
=a2-b2
当堂测试
拓展训练
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
