5.5 分式方程(2) 课件

课件19张PPT。5.5分式方程（2）第五章 分式—— 分式方程的应用复习回顾:分式方程的应用: 列分式方程解应用题．
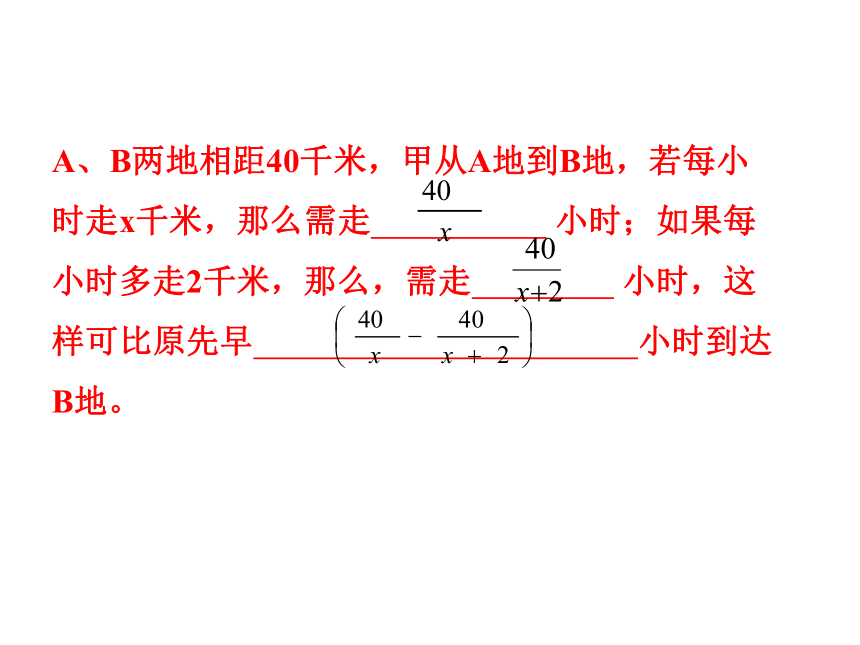
利用解分式方程把已知公式变形．A、B两地相距40千米，甲从A地到B地，若每小
时走x千米，那么需走 小时；如果每
小时多走2千米，那么，需走 小时，这
样可比原先早 小时到达
B地。 如果分数 的分子分母同时加上同一个数后,分数的值变为它的倒数,那么加上的这个数是多少?解 :设这个数为x,则可列方程 ,某车间加工1200个零件，原来每天可加工x个，则
需________天可加工完成；如果采用新工艺，工效是
原来的1.5倍，这样每天可以加工_____个，同样多的
零件只要用 天可加工完成；如果比原来快了
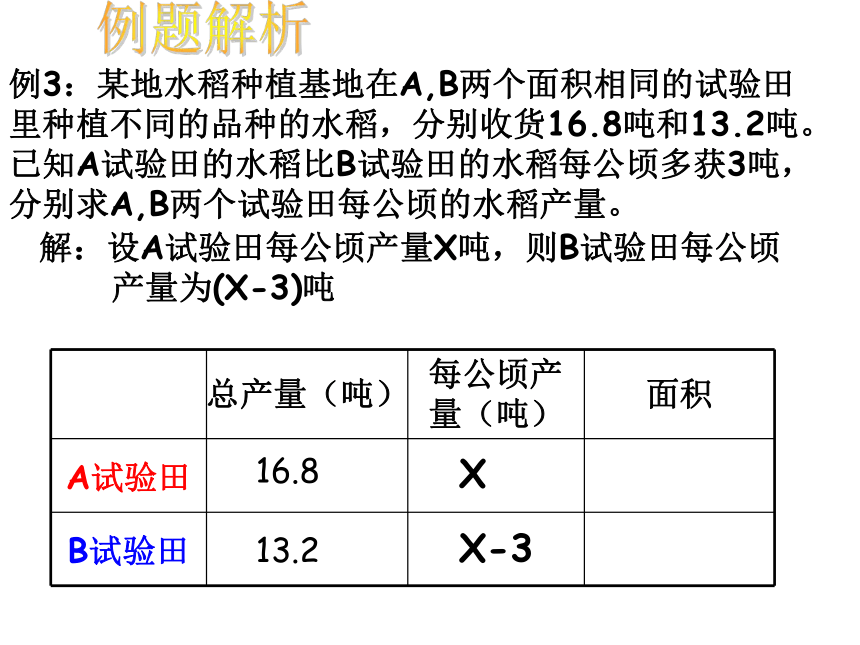
10天完成，则可列方程：1.5x例3：某地水稻种植基地在A,B两个面积相同的试验田里种植不同的品种的水稻，分别收货16.8吨和13.2吨。已知A试验田的水稻比B试验田的水稻每公顷多获3吨，分别求A,B两个试验田每公顷的水稻产量。例题解析16.813.2XX-3解：设A试验田每公顷产量X吨，则B试验田每公顷
产量为(X-3)吨例3：某地水稻种植基地在A,B两个面积相同的试验田里种植不同的品种的水稻，分别收货16.8吨和13.2吨。已知A试验田的水稻比B试验田的水稻每公顷多获3吨，分别求A,B两个试验田每公顷的水稻产量。例题解析16.813.2XX-3解：设A试验田每公顷产量X吨，则B试验田每公顷
产量为(X-3)吨解 设这种配件每只的成本降低了 x元，改进工艺前，每只售价为2×（1+25%）=2.5（元）.由题意，得化简，得解这个方程，得经检验， 是所列方程的根，且符合题意.
答：每只成本降低了0.21元例3：工厂生产一种电子配件，每只的成本为2元，毛利率为25%，后来该工厂通过改进工艺，降低了成本，在售价不变的情况下，毛利率增加了15%，问这种配件每只的成本降低了多少元？（精确到0.01元）本题等量关系是什么？例题解析毛利润＝售价－成本设这种配件每只的成本降低了　元．25%25%＋15%2 列分式方程解应用题的一般步骤1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:求出所列方程的解.
5.验:有二次检验.二次检验是:
(1)是不是所列方程的解;
(2)是否满足实际意义.
6.答:注意单位和语言完整.且答案要生活化.
甲、乙两人每小时共能做35个零件。甲、乙两人同时开始工作，当甲做了90个零件时，乙做了120个。问甲、乙每小时各做多少个零件？1、学以致用例4，照相机成像应用了一个重要原理， 其中f表示照相机镜头的焦距，u表示物体到镜头的距离，v表示明胶片（像）到镜头的距离，如果一架照相机f已固定，那么就要依靠调整U、V来使成像清晰，如果焦距f=35mm的相机，拍摄离镜头的距离u=2m的花卉，成像清晰，那么拍摄时胶片到镜头的距离v大约是多少（精确到0.1mm）？例题解析公式中，已知f,v，怎样确定u？公式变形：将求的字母看成未知数，其他字母看
成某个常数解 把f,v均看做已知数，解以u为未知数的方程：移项，得∴当f≠v时，检验：因为v,f不为零，f≠v,所以 ，是分式方程 的根.答：在已知f,v的情况下，物体到镜头的距离u可以由公式 来确定.下面的公式变形对吗？如果不对，
应怎样改正？
×试一试：1、如果 m个人完成一项工作需要d天,则(m+n)个人完成此项工作需要几天?2、某人上山和下山的路程都是s千米,上山的速度为a千米/小时,下山的速度为b千米/小时,则此人上山和下山的平均速度为( )C