浙教版七年级下册3.6 同底数幂的除法课件 (共19张PPT)
文档属性
| 名称 | 浙教版七年级下册3.6 同底数幂的除法课件 (共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 273.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-06 16:29:01 | ||
图片预览

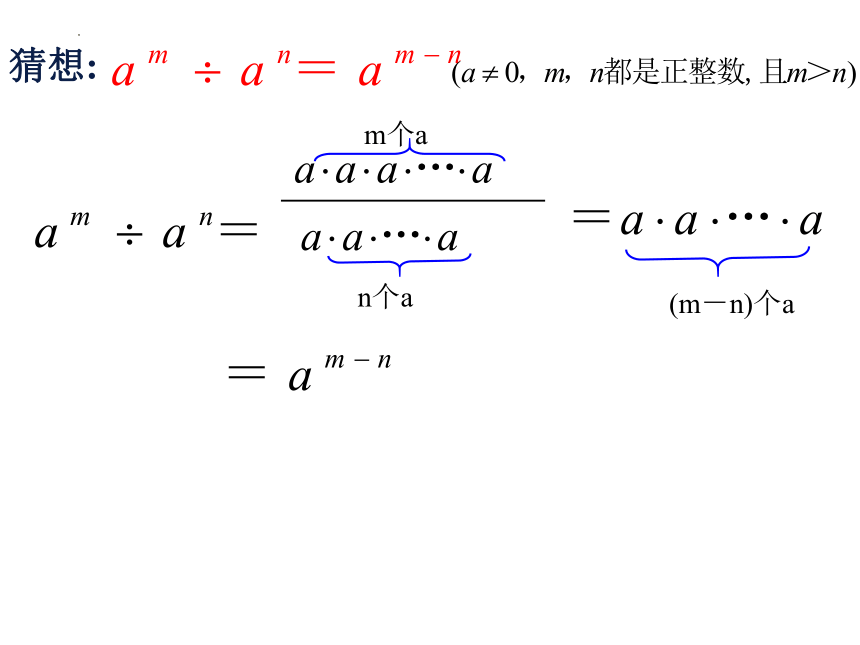




文档简介
(共19张PPT)
3.6 同底数幂的除法(1)
探究一下
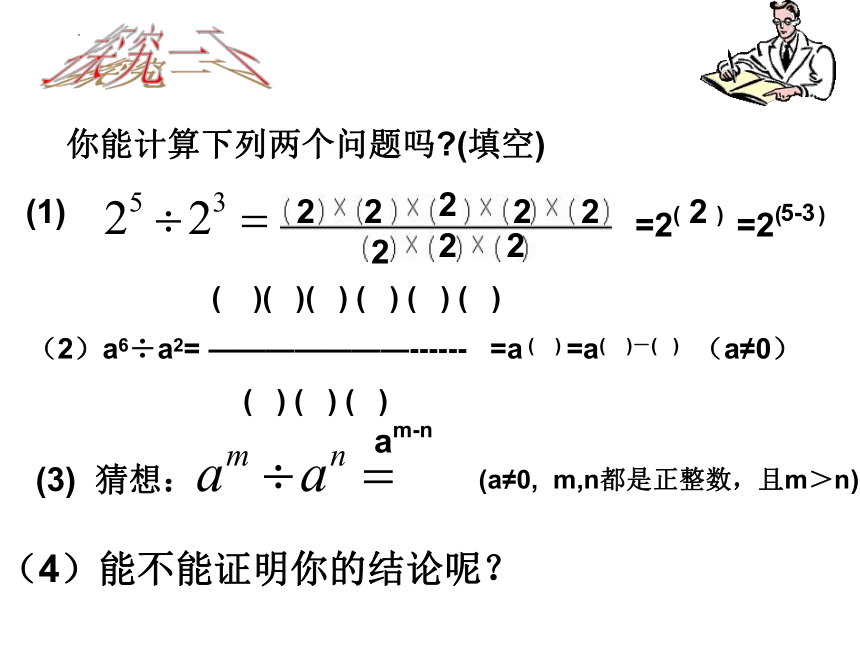
你能计算下列两个问题吗 (填空)
(1)
=2( )
=2( )
2
2
2
2
2
2
2
2
2
5-3
am-n
(3) 猜想:
(a≠0, m,n都是正整数,且m>n)
(4)能不能证明你的结论呢?
( )( )( ) ( ) ( ) ( )
(2)a6÷a2= ———————------ =a ( ) =a( )-( ) (a≠0)
( ) ( ) ( )
(m-n)个a
m个a
n个a
猜想:
am–n
不变
相减
am÷an=
同底数幂相除,底数_____, 指数______.
(a≠0,
(1) 底数相同 ;
(1)底数不变;
m、n都是正整数,
且m>n)
注意点:
结论:
条件:
(2)除法
(2) 指数相减
同底数幂的除法法则
例1.计算:
(5)
指数相等的同底数(不为0)的幂相除,商是多少 你能举例说明吗
同底数幂的乘法运算法则:
幂的乘方运算法则:
(am)n= (m、n都是正整数)
(ab)n =
an·bn
(m,n都是正整数)
积的乘方法则
amn
am · an
=
am+n
(m、n都是正整数)
同底数幂的除法运算法则:
am ÷ an = am-n m>n)
归纳总结
幂的运算法则
课内练习1、(口答)计算:
(1).s7÷s3=
(2).x10÷x8=
(3).(-t)11÷ (-t)2=
(4) (ab)5÷(ab)=
(5) (-3)6÷ (-3)2=
(6) a100÷a100=
S4
1
81
a4b4
-t9
x2
1. 下列计算对吗 为什么 错的请改正.
错
错
错
错
例2 计算:
解:(1)原式=a5-4+2=a3
(2)原式=-x7÷x2=-x7-2=-x5
(3)原式=(ab)5-2=(ab)3=a3b3
(4)原式=(a+b)6-4=(a+b)2
=a2+2ab+b2
1.乘除混合运算的顺序与有理数混合运算顺序相同(即“从左到右”).
2.若底数不同,先化为同底数,
后运用法则.
3.可以把整个代数式看作底.
4.运算结果能化简的要进行化简.
题后反思
注意:在应用同底数幂相除的法则时,底数必须是相同的,底数不同的要先利用其他的幂的运算法则转化为同底数幂的情况,再进行除法运算。
例3、计算
(ab)5÷(a2b2 ) (2)(-b)4÷(-b2)
(3) (a-b)3÷(b-a)2 (4) 323÷47
(5)
计算
(1)a7÷(a4·a2 )
(2)a5÷a·(-a)2
(3)(-x3)3÷(-x2)4
谈谈你的收获与体会
同底数幂相除的法则是:
同底数幂相除,底数不变,指数相减.
即
1.一个式子中有多种运算时,要明确运算的先后顺序.
2.底数为分数、负数、多项式时,运算过程要加括号.
(1)若n为正整数, 则 n =____
,则m =_____
(2)若 ,则
(3)若 ,求 的值
9
6
原式= ÷ ÷ ÷
提高创新题
(5)已知
求 的值.
解:原式= × ÷ × ÷
×÷
(6)已知2x-5y-4=0,求4x÷32y的值。
提高创新题
(7)若10a=20 , 10b=0.2,试求9a÷32b的值。
3、计算下列各题:
(1) x4n+1÷x 2n-1·x2n+1=
(2)已知ax=2 ay=3 则ax-y=
(3)已知ax=2 ay=3 则 a2x-y=
(4)已知am=4 an=5 求a3m-2n的值。
提高创新题
金星是太阳系八大行星中距离地球最近的行星,也是人在地球上看到的天空中最亮的一颗星。金星离地球的距离为4.2×107千米时,从金星射出的光到达地球需要多少时间?
练一练:
3.6 同底数幂的除法(1)
探究一下
你能计算下列两个问题吗 (填空)
(1)
=2( )
=2( )
2
2
2
2
2
2
2
2
2
5-3
am-n
(3) 猜想:
(a≠0, m,n都是正整数,且m>n)
(4)能不能证明你的结论呢?
( )( )( ) ( ) ( ) ( )
(2)a6÷a2= ———————------ =a ( ) =a( )-( ) (a≠0)
( ) ( ) ( )
(m-n)个a
m个a
n个a
猜想:
am–n
不变
相减
am÷an=
同底数幂相除,底数_____, 指数______.
(a≠0,
(1) 底数相同 ;
(1)底数不变;
m、n都是正整数,
且m>n)
注意点:
结论:
条件:
(2)除法
(2) 指数相减
同底数幂的除法法则
例1.计算:
(5)
指数相等的同底数(不为0)的幂相除,商是多少 你能举例说明吗
同底数幂的乘法运算法则:
幂的乘方运算法则:
(am)n= (m、n都是正整数)
(ab)n =
an·bn
(m,n都是正整数)
积的乘方法则
amn
am · an
=
am+n
(m、n都是正整数)
同底数幂的除法运算法则:
am ÷ an = am-n m>n)
归纳总结
幂的运算法则
课内练习1、(口答)计算:
(1).s7÷s3=
(2).x10÷x8=
(3).(-t)11÷ (-t)2=
(4) (ab)5÷(ab)=
(5) (-3)6÷ (-3)2=
(6) a100÷a100=
S4
1
81
a4b4
-t9
x2
1. 下列计算对吗 为什么 错的请改正.
错
错
错
错
例2 计算:
解:(1)原式=a5-4+2=a3
(2)原式=-x7÷x2=-x7-2=-x5
(3)原式=(ab)5-2=(ab)3=a3b3
(4)原式=(a+b)6-4=(a+b)2
=a2+2ab+b2
1.乘除混合运算的顺序与有理数混合运算顺序相同(即“从左到右”).
2.若底数不同,先化为同底数,
后运用法则.
3.可以把整个代数式看作底.
4.运算结果能化简的要进行化简.
题后反思
注意:在应用同底数幂相除的法则时,底数必须是相同的,底数不同的要先利用其他的幂的运算法则转化为同底数幂的情况,再进行除法运算。
例3、计算
(ab)5÷(a2b2 ) (2)(-b)4÷(-b2)
(3) (a-b)3÷(b-a)2 (4) 323÷47
(5)
计算
(1)a7÷(a4·a2 )
(2)a5÷a·(-a)2
(3)(-x3)3÷(-x2)4
谈谈你的收获与体会
同底数幂相除的法则是:
同底数幂相除,底数不变,指数相减.
即
1.一个式子中有多种运算时,要明确运算的先后顺序.
2.底数为分数、负数、多项式时,运算过程要加括号.
(1)若n为正整数, 则 n =____
,则m =_____
(2)若 ,则
(3)若 ,求 的值
9
6
原式= ÷ ÷ ÷
提高创新题
(5)已知
求 的值.
解:原式= × ÷ × ÷
×÷
(6)已知2x-5y-4=0,求4x÷32y的值。
提高创新题
(7)若10a=20 , 10b=0.2,试求9a÷32b的值。
3、计算下列各题:
(1) x4n+1÷x 2n-1·x2n+1=
(2)已知ax=2 ay=3 则ax-y=
(3)已知ax=2 ay=3 则 a2x-y=
(4)已知am=4 an=5 求a3m-2n的值。
提高创新题
金星是太阳系八大行星中距离地球最近的行星,也是人在地球上看到的天空中最亮的一颗星。金星离地球的距离为4.2×107千米时,从金星射出的光到达地球需要多少时间?
练一练:
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
