浙教版七年级下册3.4乘法公式 课件 (共14张PPT)
文档属性
| 名称 | 浙教版七年级下册3.4乘法公式 课件 (共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 163.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-06 16:59:50 | ||
图片预览






文档简介
(共14张PPT)
3.4 乘法公式(2)
做一做
图1
a
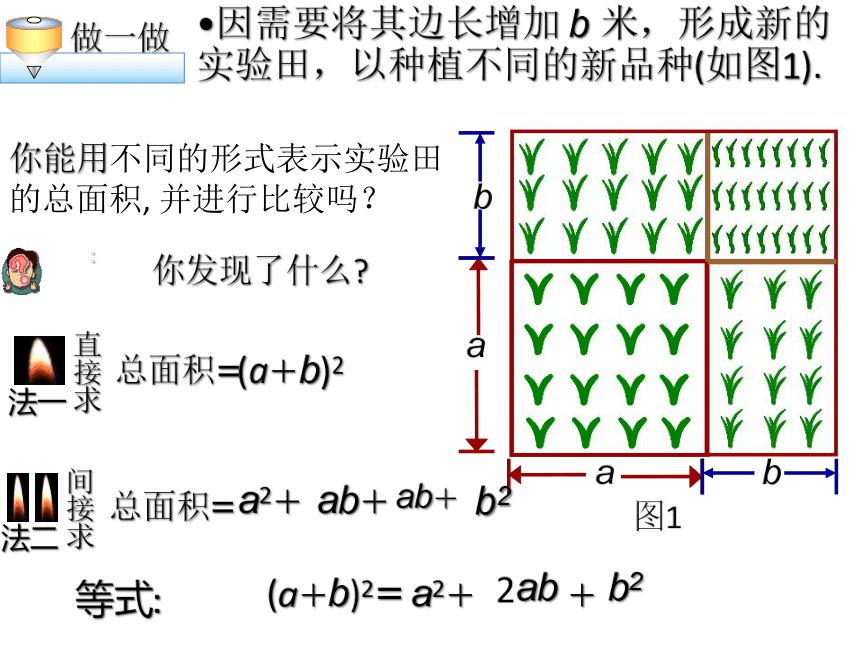
因需要将其边长增加 b 米,形成新的实验田,以种植不同的新品种(如图1).
你能用不同的形式表示实验田的总面积, 并进行比较吗?
a
b
b
法一
直
接
求
总面积=
(a+b)2
法二
间
接
求
总面积=
a2+
ab+
ab+
b2
(a+b)2=
a2+
ab
+
b2
你发现了什么
探索:
2
等式:
(a+b)2=a2+2ab+b2
两数和的平方,等于它们的平方和加上它们乘积的2倍.
两数和的完全平方公式
归纳新知
( a+ b)2=a2+2 a b+ b2
(x+2y)2=
x2+2·x·2y+(2y)2
=x2+4xy+4y2
(a+1 )2 = ( )2 +2( )( )+ ( )2
(-4x+5y)2 =( )2 +2( )( )+ ( )2
=
(2) (2a+3b ) 2 = ( )2 +2( )( )+ ( )2
利用和的完全平方公式计算:
=
=
基础巩固
自主探索
你能计算(a b)2吗
完全平方差公式:
(a b)2 = a2 2ab+b2
两数差的平方,等于这两数的平方和,减去这两数积的2倍.
6
(a+b)2=a2+2ab+b2
(a b)2=a2 2ab+b2
完全平方公式
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
首平方,尾平方,首尾两倍放中间
基础练习
利用完全平方公式计算:
(1) (2a+5)2 ; (2) (x-2y)2;
(3) (-2a+b)2 ; (4) (-3x-2y)2
(5)10012
8
下列各式的计算是否有错?错的请改正。
(1) (x+y)2 = x2 +y2
(2) (a –b)2 = a2 -b2
(4) (a+2b)2 = a2+2ab+2b2
(3) (-x+ 1)2 = x2 – 2x+1
(5) (2+x)2 = 2 + 4x+ x2
基础练习
+
比较平方差公式和完全平方公式:
(a-b)(a+b)= a2-b2
( a+ b)2=a2+2 a b+ b2
( a- b)2=a2-2 a b+ b2
公式 相乘多项式的特征 展开式项数
平方差公式 一项相同,另一项相反 2项
完全平方公式 两项都相同 3项
选择适当的公式计算:
(1)(2x-1)(-1+2x); (2) (-2x-y)(2x-y)
(3) (-a+5)(-a-5); (4) (ab-1)(-ab+1)
巩固练习
一花农有2块正方形茶花苗圃,边长分别为30.1m,29.5m。现将这2块苗圃的边长都增加1.5m,求各苗圃的面积分别增加了多少m 。
解:设原正方形苗圃的边长为am,边长都增1.5m,
新正方形的边长为(a+1.5)m,
(a+1.5)2-a2=a2+3a+2.25-a2=3a+2.25
当a=30.1时,3a+2.25=3×30.1+2.25=92.55
当a=29.5时,3a+2.25=3×29.5+2.25=90.75
答:苗圃的面积分别增加了92.55m2,90.75m2
完全平方公式
口诀:首平方,尾平方,首尾两倍中间放
我们把完全平方和公式与完全平方差公式统称为完全平方公式(也叫乘法公式)
小结
在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2;
1.如果x2-6x+N是一个完全平方式,那么N是( )
(A )11 (B)9 (C)-11 (D)-9
2.如果多项式x2 +kx+9是完全平方式,求k 的值。
拓展提升
变式拓展
1.已知:x +y =3 ; x y =2 求 x2+y2 ; (x y)2 的值
3.4 乘法公式(2)
做一做
图1
a
因需要将其边长增加 b 米,形成新的实验田,以种植不同的新品种(如图1).
你能用不同的形式表示实验田的总面积, 并进行比较吗?
a
b
b
法一
直
接
求
总面积=
(a+b)2
法二
间
接
求
总面积=
a2+
ab+
ab+
b2
(a+b)2=
a2+
ab
+
b2
你发现了什么
探索:
2
等式:
(a+b)2=a2+2ab+b2
两数和的平方,等于它们的平方和加上它们乘积的2倍.
两数和的完全平方公式
归纳新知
( a+ b)2=a2+2 a b+ b2
(x+2y)2=
x2+2·x·2y+(2y)2
=x2+4xy+4y2
(a+1 )2 = ( )2 +2( )( )+ ( )2
(-4x+5y)2 =( )2 +2( )( )+ ( )2
=
(2) (2a+3b ) 2 = ( )2 +2( )( )+ ( )2
利用和的完全平方公式计算:
=
=
基础巩固
自主探索
你能计算(a b)2吗
完全平方差公式:
(a b)2 = a2 2ab+b2
两数差的平方,等于这两数的平方和,减去这两数积的2倍.
6
(a+b)2=a2+2ab+b2
(a b)2=a2 2ab+b2
完全平方公式
两个数的和(或差)的平方,等于它们的平方和,加上(或减去)它们的积的2倍。
首平方,尾平方,首尾两倍放中间
基础练习
利用完全平方公式计算:
(1) (2a+5)2 ; (2) (x-2y)2;
(3) (-2a+b)2 ; (4) (-3x-2y)2
(5)10012
8
下列各式的计算是否有错?错的请改正。
(1) (x+y)2 = x2 +y2
(2) (a –b)2 = a2 -b2
(4) (a+2b)2 = a2+2ab+2b2
(3) (-x+ 1)2 = x2 – 2x+1
(5) (2+x)2 = 2 + 4x+ x2
基础练习
+
比较平方差公式和完全平方公式:
(a-b)(a+b)= a2-b2
( a+ b)2=a2+2 a b+ b2
( a- b)2=a2-2 a b+ b2
公式 相乘多项式的特征 展开式项数
平方差公式 一项相同,另一项相反 2项
完全平方公式 两项都相同 3项
选择适当的公式计算:
(1)(2x-1)(-1+2x); (2) (-2x-y)(2x-y)
(3) (-a+5)(-a-5); (4) (ab-1)(-ab+1)
巩固练习
一花农有2块正方形茶花苗圃,边长分别为30.1m,29.5m。现将这2块苗圃的边长都增加1.5m,求各苗圃的面积分别增加了多少m 。
解:设原正方形苗圃的边长为am,边长都增1.5m,
新正方形的边长为(a+1.5)m,
(a+1.5)2-a2=a2+3a+2.25-a2=3a+2.25
当a=30.1时,3a+2.25=3×30.1+2.25=92.55
当a=29.5时,3a+2.25=3×29.5+2.25=90.75
答:苗圃的面积分别增加了92.55m2,90.75m2
完全平方公式
口诀:首平方,尾平方,首尾两倍中间放
我们把完全平方和公式与完全平方差公式统称为完全平方公式(也叫乘法公式)
小结
在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2;
1.如果x2-6x+N是一个完全平方式,那么N是( )
(A )11 (B)9 (C)-11 (D)-9
2.如果多项式x2 +kx+9是完全平方式,求k 的值。
拓展提升
变式拓展
1.已知:x +y =3 ; x y =2 求 x2+y2 ; (x y)2 的值
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
