浙教版七年级下册3.2单项式的乘法课件 (共14张PPT)
文档属性
| 名称 | 浙教版七年级下册3.2单项式的乘法课件 (共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 938.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-07 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
3.2单项式的乘法
回顾:
1、同底数幂相乘的运算法则:
am·an=am+n(m,n都是正整数)
2、幂的乘方运算法则
(am)n=amn(m,n都是正整数)
3、积的乘方法则
( ab)n = an·bn (n为正整数)
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘。
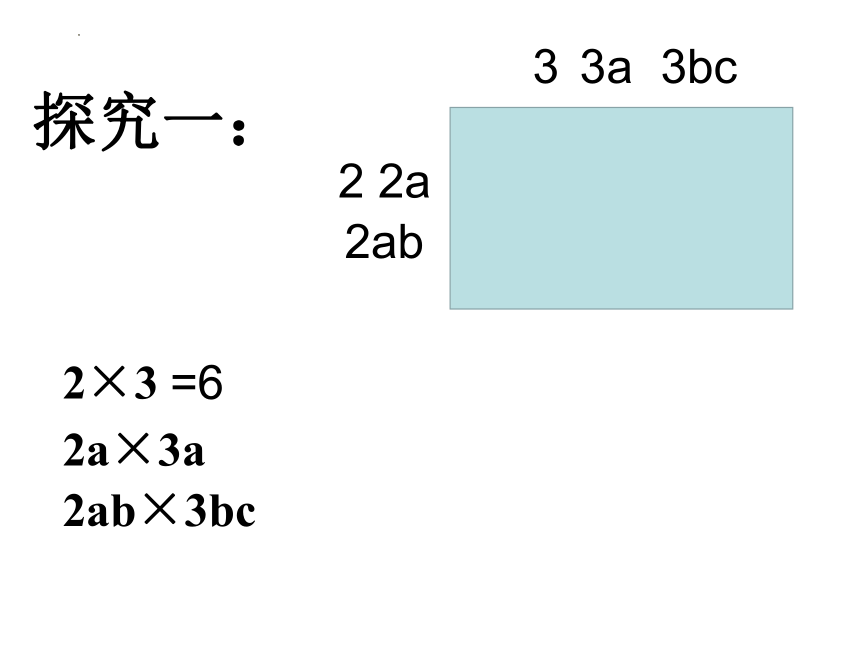
探究一:
2
3
3a
2a
2ab
3bc
2×3
2a×3a
2ab×3bc
=6
(2)4x3 · 2xy =
8x4y2
尝试解答:
计算:(-2abc) · ( 4ab2 )
解:原式=
=-8a2 b3 c
[(-2) × 4 )]
c
(a a)
2
(b b )
各系数因数
结合成一组
相同的字母
结合成一组
不能遗漏
单项式与单项式相乘,把他们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式。
你能叙述单项式与单项式相乘的法则吗?
单项式与单项式相乘,把他们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式。
我们一起来试一试:
(1) 3ab·2a b
(2)
(3) 5x2y·(-2xy3z4)
(4) (-6ay )·(-a )2
(5) (-3x) ·(5xy)
(6) (2x10 )(6x10 ) ·107
注意运算顺序
注意符号
注意指数运算
注意不要遗漏
单项式乘法中要注意的几点
求系数的积,应注意符号;
相同字母因式相乘,是同底数幂的乘法,底数不变,指数相加;
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏;
单项式乘以单项式的结果仍然是一个单项式,结果要把系数写在字母因式的前面;
注意符号
不要遗漏
注意指数运算
注意运算顺序
下列题目做对了吗?
8a5
6x8
-18x3y
( )
( )
( )
( )
(1)
(2)
(3)
(4)
(6)
(5)
( )
( )
7y4
探究2
一幅画的尺寸如图所示
(1)请用两种不同的方法表示这幅画的面积
(2)你能总结出单项式与多项式相乘的 运算规律吗?
a(b-2m)
ab-2am
b
a
m
m
用单项式分别去乘多项式的每一项,再把所得的积相加。
实质
-----分配律!
a(b+c)=ab+ac
单项式与多项式相乘,就是用单项式乘多项式的每一项,再把所得的积相加。
单项式与单项式相乘,把他们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的形式。
计算下列式子:
计算下列式子:
(4) (x – 3y)
(3)
(1) (-5a2b3).(-2bc)
(6) -2(– 2x) ·(x – 3y)
(5)x(4x2-x+6)-2x(x2-1)
(-2x)
数形结合思想
转化思想
单项式与单项式相乘的法则
单项式与多项式相乘的法则
思想方法收获
知识收获
今天我们一起学习了什么?
拓展提升:
已知x2y=3,求2xy(x5y2-3x3y-4x)的值.
再见
课堂小结
2.单项式与多项式相乘,就是用
单项式去乘多项式的每一项,再
把所得的积相加.
1.单项式与单项式相乘,把它们
的系数、同底数幂分别相乘,
其余字母连同它的指数不变,
作为积的因式.
3.2单项式的乘法
回顾:
1、同底数幂相乘的运算法则:
am·an=am+n(m,n都是正整数)
2、幂的乘方运算法则
(am)n=amn(m,n都是正整数)
3、积的乘方法则
( ab)n = an·bn (n为正整数)
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘。
探究一:
2
3
3a
2a
2ab
3bc
2×3
2a×3a
2ab×3bc
=6
(2)4x3 · 2xy =
8x4y2
尝试解答:
计算:(-2abc) · ( 4ab2 )
解:原式=
=-8a2 b3 c
[(-2) × 4 )]
c
(a a)
2
(b b )
各系数因数
结合成一组
相同的字母
结合成一组
不能遗漏
单项式与单项式相乘,把他们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式。
你能叙述单项式与单项式相乘的法则吗?
单项式与单项式相乘,把他们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式。
我们一起来试一试:
(1) 3ab·2a b
(2)
(3) 5x2y·(-2xy3z4)
(4) (-6ay )·(-a )2
(5) (-3x) ·(5xy)
(6) (2x10 )(6x10 ) ·107
注意运算顺序
注意符号
注意指数运算
注意不要遗漏
单项式乘法中要注意的几点
求系数的积,应注意符号;
相同字母因式相乘,是同底数幂的乘法,底数不变,指数相加;
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏;
单项式乘以单项式的结果仍然是一个单项式,结果要把系数写在字母因式的前面;
注意符号
不要遗漏
注意指数运算
注意运算顺序
下列题目做对了吗?
8a5
6x8
-18x3y
( )
( )
( )
( )
(1)
(2)
(3)
(4)
(6)
(5)
( )
( )
7y4
探究2
一幅画的尺寸如图所示
(1)请用两种不同的方法表示这幅画的面积
(2)你能总结出单项式与多项式相乘的 运算规律吗?
a(b-2m)
ab-2am
b
a
m
m
用单项式分别去乘多项式的每一项,再把所得的积相加。
实质
-----分配律!
a(b+c)=ab+ac
单项式与多项式相乘,就是用单项式乘多项式的每一项,再把所得的积相加。
单项式与单项式相乘,把他们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的形式。
计算下列式子:
计算下列式子:
(4) (x – 3y)
(3)
(1) (-5a2b3).(-2bc)
(6) -2(– 2x) ·(x – 3y)
(5)x(4x2-x+6)-2x(x2-1)
(-2x)
数形结合思想
转化思想
单项式与单项式相乘的法则
单项式与多项式相乘的法则
思想方法收获
知识收获
今天我们一起学习了什么?
拓展提升:
已知x2y=3,求2xy(x5y2-3x3y-4x)的值.
再见
课堂小结
2.单项式与多项式相乘,就是用
单项式去乘多项式的每一项,再
把所得的积相加.
1.单项式与单项式相乘,把它们
的系数、同底数幂分别相乘,
其余字母连同它的指数不变,
作为积的因式.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
