浙教版七年级下册 3.3多项式的乘法(一) 课件(共15张PPT)
文档属性
| 名称 | 浙教版七年级下册 3.3多项式的乘法(一) 课件(共15张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-09 09:51:05 | ||
图片预览



文档简介
(共15张PPT)
3.3多项式的乘法(一)
浙教版 七(下)
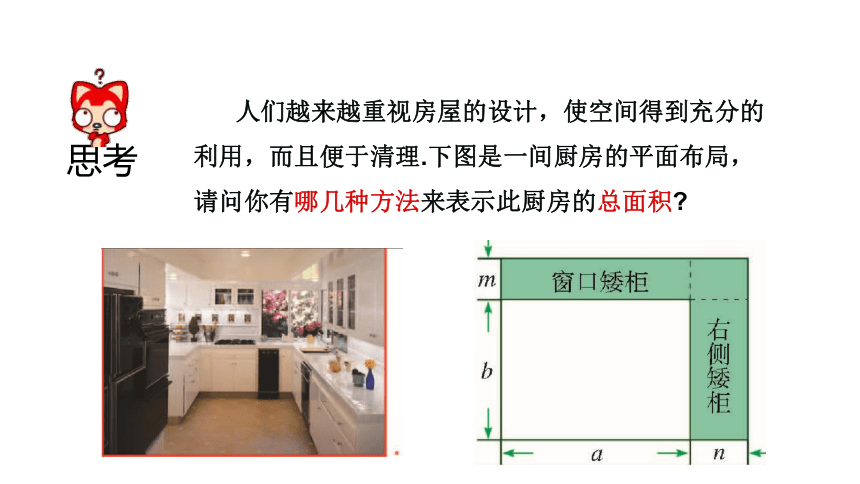
人们越来越重视房屋的设计,使空间得到充分的利用,而且便于清理.下图是一间厨房的平面布局,请问你有哪几种方法来表示此厨房的总面积
思考
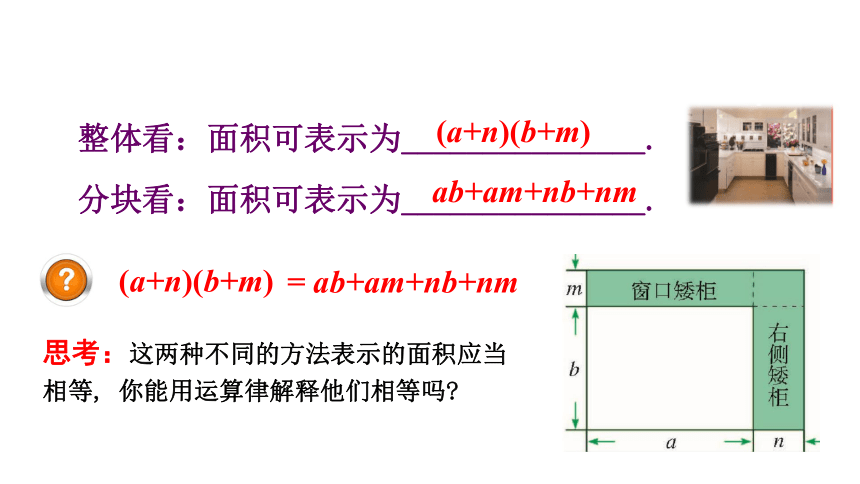
整体看:面积可表示为_______________.
分块看:面积可表示为_______________.
(a+n)(b+m)
ab+am+nb+nm
(a+n)(b+m)
= ab+am+nb+nm
思考:这两种不同的方法表示的面积应当相等, 你能用运算律解释他们相等吗
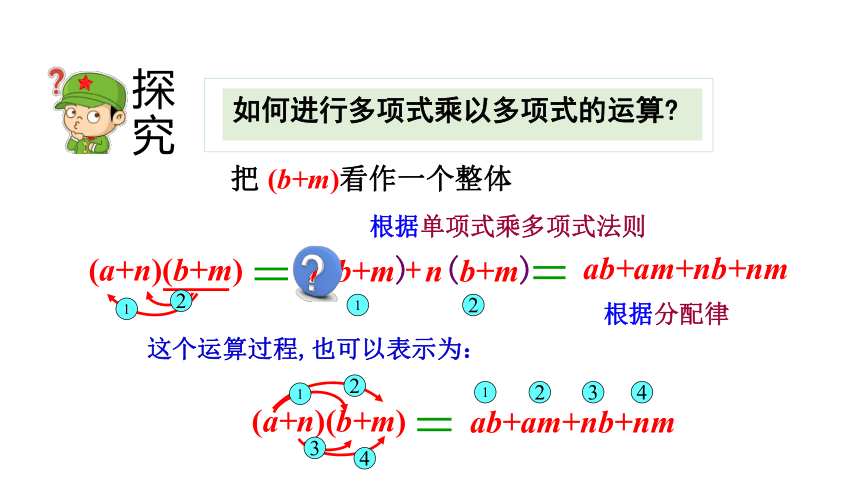
根据单项式乘多项式法则
a(b+m)
n(b+m)
+
根据分配律
把 (b+m)看作一个整体
(a+n)(b+m)
ab+am+nb+nm
这个运算过程,也可以表示为:
探究
如何进行多项式乘以多项式的运算
(a+n)(b+m)
ab+am+nb+nm
1
2
3
4
1
2
3
4
1
2
1
2
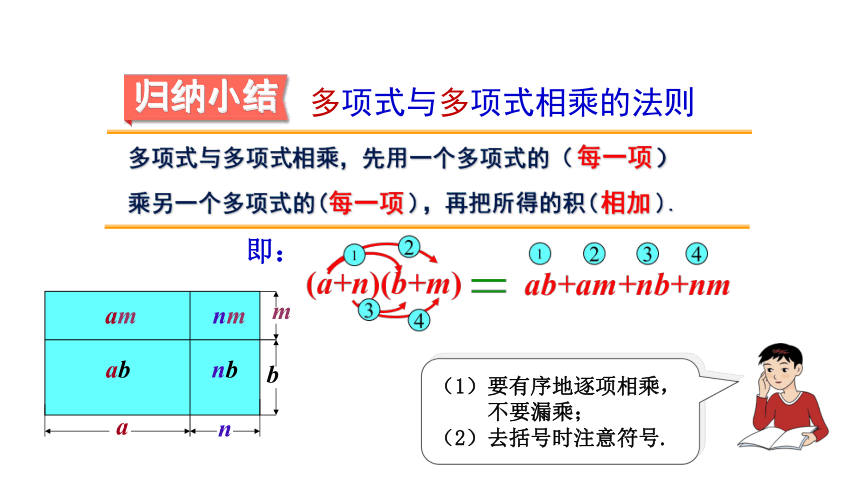
多项式与多项式相乘的法则
多项式与多项式相乘,先用一个多项式的( )
乘另一个多项式的( ),再把所得的积( ).
每一项
(1)要有序地逐项相乘,
不要漏乘;
(2)去括号时注意符号.
归纳小结
每一项
相加
即:
a
n
b
m
ab
am
nm
nb
(2) (3x 1) ( x+3)
例1 计算:
注意:化简结果要最简
(即不再含有同类项)
=3x2
-6xy
+xy
-2y2
=3x2-5xy-2y2
=3x2
=3x2+8x-3
+9x
-x
-3
(1) (3x + y) (x 2y)
思考:多项式乘以多项式,展开后项数有什么规律?
答:在合并同类项之前,展开式的项数恰好
等于两个多项式的项数的积。
错
勿漏乘,项数为2×2=4
错
“-”要特别注意
错
同类项要合并
如果有错,请改正,并说出错误原因.
练一练
计算:
解
解
多项式与多项式相乘的结果中,
如果有同类项,要把同类项合并.
注 意
(1)(2a+b)2
(2)(x-2y)(x-y-3)
+b2
+b2
=4a2
+2ab
+2ab
=4a2
+4ab
(1)(2a+b)2
+6y
=x2-3xy-3x+2y2+6y
=x2
-xy
-3x
-2xy
+2y2
(2)(x-2y)(x-y-3)
=(2a+b) (2a+b)
(2a 3)(3a + 1) 6a (a 4),其中a =
例2 先化简,再求值:
1. 把每个积都添上括号,特别是积的前面是“-”号时;
2. 去括号时要注意符号,化简结果要最简.
注 意
“-”要特别注意
练一练
1.化简:
解: (1) 原式
(1) (2x 1)( 3x) (1 3x)(1+2x)
(2) 2(x 8)(x 5) (2x 1)(x+2)
解: (2) 原式
练一练
解:
当x = 2 时,原式=6×2 9 = 3 .
如图,有一块边长为a的正方形花圃,两横一纵宽度均为b的三条人行通道把花圃分割成6块.问该花圃的实际种花面积是多少?
思考:该花圃的实际种花面积比原正方形花圃面积减少了多少?
解:
例3
一幅宣传画的长为a(cm),宽为b(cm). 把它贴在一块长方形木板上,四周刚好留出2cm的边框宽. 请你算一算,这块木板的面积是多少。
a
b
2
2
解: S=(a+4)(b+4)
=ab+4a+4b+16
练一练
1.多项式与多项式相乘的法则
3. 数学思想:数形结合、整体思想、化归思想.
2.法则应用的注意事项:
(1)要有序地逐项相乘,不要漏乘;
(2)去括号时注意符号;
(3)化简结果要最简(即不含有同类项)
课堂小结
1. 计算:
(1)(x+2)(x+3)
(2)(x+3)(x 4)
(3)(x-3)(x 4)
= x2 + 5x +6
= x2 x 12
= x2 7x +12
2. 观察上面三题的特点,你发现有什么规律?
按你发现的规律填空:
3. 若(x+m)(x-2)=x2+nx-6对x的任何值都成立,
你能快速求出m,n的值吗?
(x+a)(x+b)=x2+( + ) x+
a
b
ab
解:m=3,n=1.
拓展应用
3.3多项式的乘法(一)
浙教版 七(下)
人们越来越重视房屋的设计,使空间得到充分的利用,而且便于清理.下图是一间厨房的平面布局,请问你有哪几种方法来表示此厨房的总面积
思考
整体看:面积可表示为_______________.
分块看:面积可表示为_______________.
(a+n)(b+m)
ab+am+nb+nm
(a+n)(b+m)
= ab+am+nb+nm
思考:这两种不同的方法表示的面积应当相等, 你能用运算律解释他们相等吗
根据单项式乘多项式法则
a(b+m)
n(b+m)
+
根据分配律
把 (b+m)看作一个整体
(a+n)(b+m)
ab+am+nb+nm
这个运算过程,也可以表示为:
探究
如何进行多项式乘以多项式的运算
(a+n)(b+m)
ab+am+nb+nm
1
2
3
4
1
2
3
4
1
2
1
2
多项式与多项式相乘的法则
多项式与多项式相乘,先用一个多项式的( )
乘另一个多项式的( ),再把所得的积( ).
每一项
(1)要有序地逐项相乘,
不要漏乘;
(2)去括号时注意符号.
归纳小结
每一项
相加
即:
a
n
b
m
ab
am
nm
nb
(2) (3x 1) ( x+3)
例1 计算:
注意:化简结果要最简
(即不再含有同类项)
=3x2
-6xy
+xy
-2y2
=3x2-5xy-2y2
=3x2
=3x2+8x-3
+9x
-x
-3
(1) (3x + y) (x 2y)
思考:多项式乘以多项式,展开后项数有什么规律?
答:在合并同类项之前,展开式的项数恰好
等于两个多项式的项数的积。
错
勿漏乘,项数为2×2=4
错
“-”要特别注意
错
同类项要合并
如果有错,请改正,并说出错误原因.
练一练
计算:
解
解
多项式与多项式相乘的结果中,
如果有同类项,要把同类项合并.
注 意
(1)(2a+b)2
(2)(x-2y)(x-y-3)
+b2
+b2
=4a2
+2ab
+2ab
=4a2
+4ab
(1)(2a+b)2
+6y
=x2-3xy-3x+2y2+6y
=x2
-xy
-3x
-2xy
+2y2
(2)(x-2y)(x-y-3)
=(2a+b) (2a+b)
(2a 3)(3a + 1) 6a (a 4),其中a =
例2 先化简,再求值:
1. 把每个积都添上括号,特别是积的前面是“-”号时;
2. 去括号时要注意符号,化简结果要最简.
注 意
“-”要特别注意
练一练
1.化简:
解: (1) 原式
(1) (2x 1)( 3x) (1 3x)(1+2x)
(2) 2(x 8)(x 5) (2x 1)(x+2)
解: (2) 原式
练一练
解:
当x = 2 时,原式=6×2 9 = 3 .
如图,有一块边长为a的正方形花圃,两横一纵宽度均为b的三条人行通道把花圃分割成6块.问该花圃的实际种花面积是多少?
思考:该花圃的实际种花面积比原正方形花圃面积减少了多少?
解:
例3
一幅宣传画的长为a(cm),宽为b(cm). 把它贴在一块长方形木板上,四周刚好留出2cm的边框宽. 请你算一算,这块木板的面积是多少。
a
b
2
2
解: S=(a+4)(b+4)
=ab+4a+4b+16
练一练
1.多项式与多项式相乘的法则
3. 数学思想:数形结合、整体思想、化归思想.
2.法则应用的注意事项:
(1)要有序地逐项相乘,不要漏乘;
(2)去括号时注意符号;
(3)化简结果要最简(即不含有同类项)
课堂小结
1. 计算:
(1)(x+2)(x+3)
(2)(x+3)(x 4)
(3)(x-3)(x 4)
= x2 + 5x +6
= x2 x 12
= x2 7x +12
2. 观察上面三题的特点,你发现有什么规律?
按你发现的规律填空:
3. 若(x+m)(x-2)=x2+nx-6对x的任何值都成立,
你能快速求出m,n的值吗?
(x+a)(x+b)=x2+( + ) x+
a
b
ab
解:m=3,n=1.
拓展应用
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
