3.1 同底数幂的乘法（1）课件

课件18张PPT。3.1同底数幂的乘法（1）泰顺六中 翁怀新2013年4月8日102 × 105 × 10 7 等于多少呢？3×105× 3×107= 9×102×105 × 107 102×（千米）复习回顾 （结果写成幂的形式）
（1）这个底座的底面积为＿＿＿＿＿；
（2）这个底座的体积为＿＿＿＿＿；
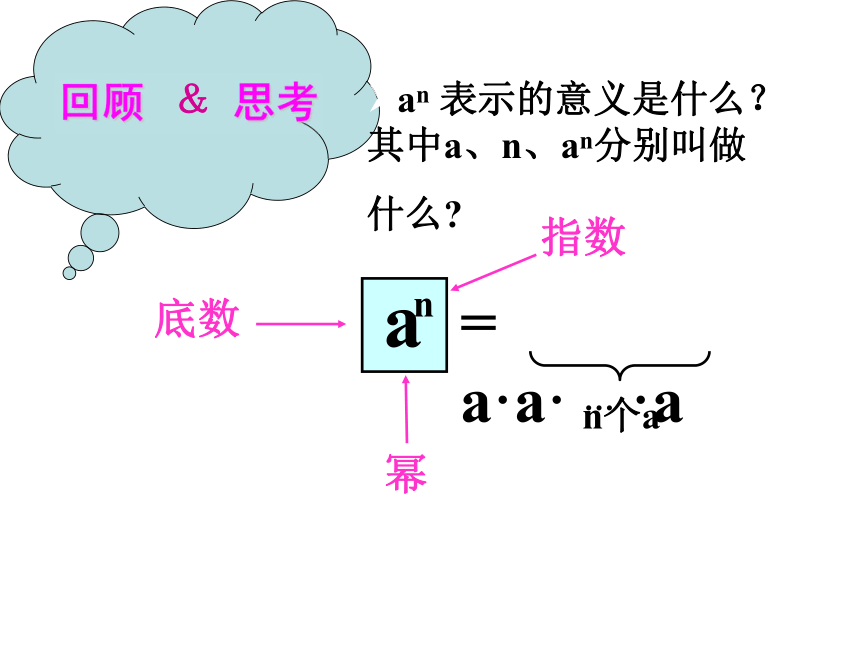
幂指数复习回顾指数幂底数an 表示的意义是什么？其中a、n、an分别叫做
什么?
回顾 思考＆合作学习 23×22 = ( ) ×( )
=________________=2( ) =2( )+( )(2)102×105 = ( ) ×( )
=_______________________________
=10( ) =10( )+( )(3) a4 · a3 = ( ) · ( )
=_________ =a( ) =a( )+( )2 × 2 × 22 × 22 × 2 × 2 × 2 × 253210×1010 × 10 × 10 × 10 × 1010 × 10 × 10 × 10 × 10 × 10 × 10725aaaaaaaaaaaaaa743请同学们根据自己的理解，完成下列填空
思考：观察上面各题左右两边，底数、指数有什么关系？
猜想: am · an= ? (当m、n都是正整数)
　　分组讨论，并尝试说明你的猜想是正确的。 猜想: am · an = (当m、n都是正整数) am · an =m个an个a= aa…a=am+n(m+n)个a 同底数幂相乘,底数不变,指数相加
即 am · an = am+n (m、n都是正整数)（aa…a）（aa…a）am+n?同底数幂的乘法法则:对运算性质的剖析： 条件：①乘法 ②同底数幂
结果：①底数不变 ②指数相加例1 计算下列各式,结果用幂的形式表示 (1) 7 8 × 7 3 (2) (-2) 8 × (-2)7
解: (1) 7 8 × 7 3 = 7 8+3 = 7 11
(2) (-2) 8 × (-2)7 = (-2) 8 +7 = (-2)15 = -215
(3) x3 · x5 = x3+5 = x8
(4) (a-b)2 (a-b) = (a-b)2+1 = (a-b)3 (3) x3 · x5 (4) (a-b)2 (a-b)做一做变式1：73×(－7)8 ？当底数不同时，该怎么办呢？
变式2：(－7)3×78 ？底数不同时，先将底数化为一致开头问题中第100颗行星与地球之间的距离约为 千米。9×102×105 × 107 9 ×1014=9×102+5+7=9 ×1014（千米）一年以3×107 秒计算，第100颗行星与地球之间
的距离约为多少千米？
下面的计算对不对？如果不对，怎样改正？
（1）b5 · b5= 2b5 （ ） （2）b5 + b5 = b10 （ ）
m + m3 = m + m3 b5 · b5= b10 b5 + b5 = 2b5 x2 · x3 = x5 (-7)8 · 73 = 711 a · a6 = a7× × × ×××? 判一判 ? （3）x2 ·x3 = x6 ( ) （4）(-7)8 · 7 3 = (-7)11 ( )（5）a · a6 = a6 ( ) （6）m + m3 = m4 ( ) 通过上面的练习你认为同底数幂的乘法法则的应用应注意什么?1.同底数幂相乘时,指数是相加的
2.注意 am · an 与am + an的区别
3.不能疏忽指数为1的情况
例2 我国自行研制的“神威Ⅰ”计算机的峰值运算速度达到每秒3840亿次。如果按这个速度工作一整天，那么它能运算多少次？ （结果保留3个有效数字）解：3840亿次=3.84×103×108次24时=24×3.6×103秒（3.84×103×108 ）×（24×3.6×103）=（3.84×24×3.6）×（103×108×103）= 331.776×1014≈ 3.32×1016（次）答：它一天约能运算3.32×1016次.am · an · ap 等于什么？想一想:猜想:练一练:运用同底数幂的乘法法则计算下
列各式,并用幂的形式表示结果： 2 7 × 23 (2) (-3) 4 × (-3)7
(3) (-5) 2 × (-5)3 × 54 (4) (x+y) 3× (x+y)解: (1) 2 7 × 23 = 27+3 = 210 (2) (-3) 4 × (-3)7 = (-3) 4+7 = (-3)11
(3) (-5) 2 × (-5)3 × 54 = (-5) 2+3+4 =(-5)9 (4) (x+y) 3× (x+y)= (x+y) 3+1= (x+y)4课堂小结同底数幂的乘法性质：底数 ，指数 .不变相加幂的意义:注意：同底数幂相乘时通过本节课的学习，你在知识上有哪些收获，你学到了哪些方法？四、提炼小结 完善结构
同底数幂相乘，　
底数　　 指数　
am · an = am+n (m、n正整数)小结我学到了什么？ 知识　 　　方法　　“特殊→一般→特殊”
　 例子 公式 应用不变，相加。填空：
（1）x5 ·（ ）=　x 8 （2）a ·（ ）=　a6
（3）x · x3（ ）= x7 （4）xm ·（　 ）＝ｘ3m
x3a5 x3ｘ2m真棒！真不错！你真行！太棒了！极限挑战一填空：
（1） 8 = 2x，则 x = ；
（2） 8× 4 = 2x，则 x = ；
（3） 3×27×9 = 3x，则 x = .35623 23 3253622 × = 33 32 × ×=极限挑战二布置作业1.必做题： 课本第61页 第1-5题
作业本1分册第12页
2.选做题：课时特训第31到32页